【C语言】数据结构——排序三（归并与计数排序）

💗个人主页💗
?个人专栏——数据结构学习?
💫点击关注🤩一起学习C语言💯💫

导读：

我们在前面学习了排序，包括直接插入排序，希尔排序，选择排序，堆排序，冒泡排序和快排。
今天我们来讲一讲归并排序和计数排序。
关注博主或是订阅专栏，掌握第一消息。

1. 归并排序

1.1 基本思想

归并排序的基本思想是将待排序的数组分成两个较小的子数组，然后递归地对这两个子数组进行排序，最后将两个有序的子数组合并成一个有序的数组。

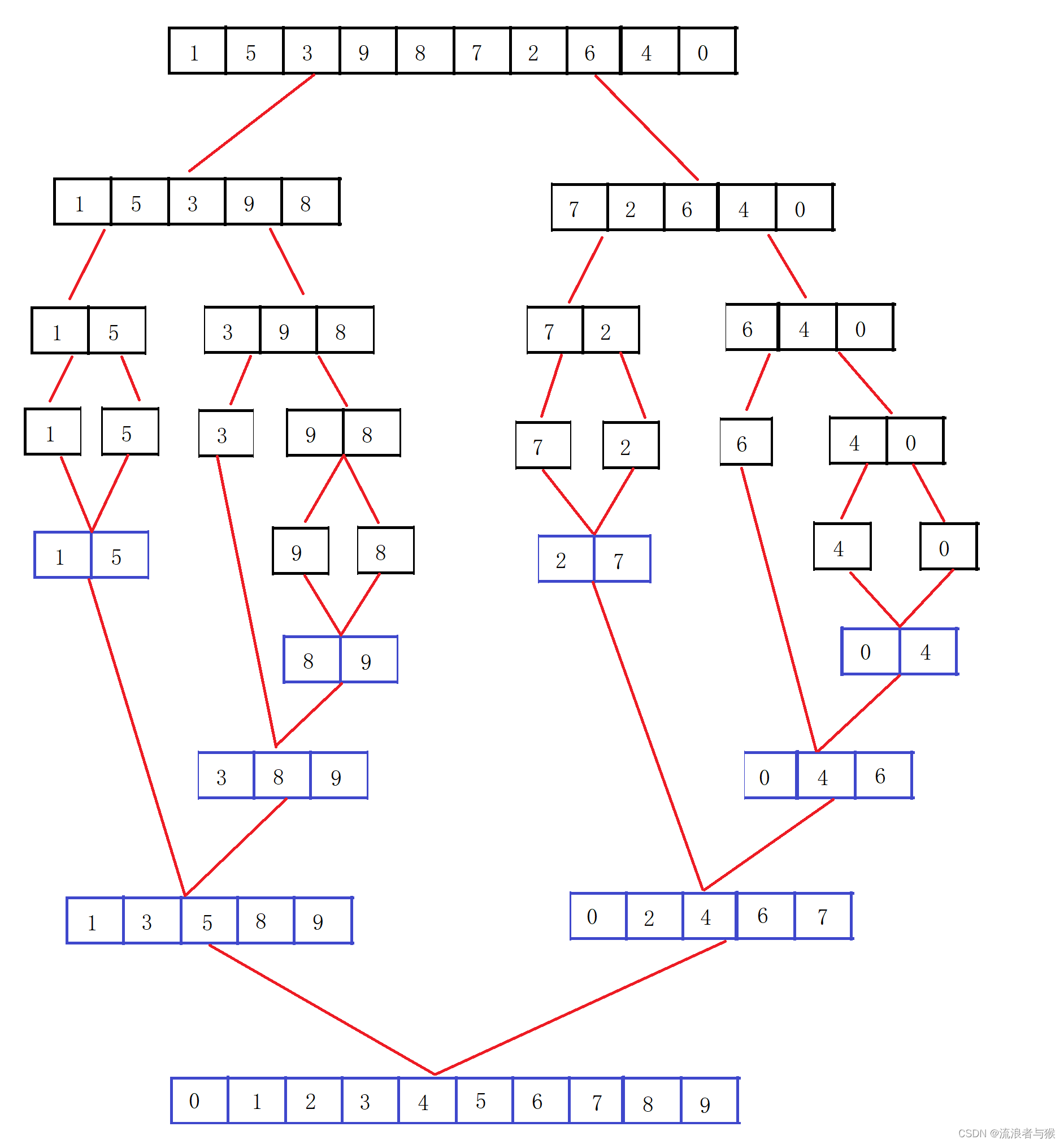
1. 将待排序数组分成两个较小的子数组，直到子数组中只剩下一个元素。
2. 对两个子数组分别进行归并排序，即递归调用归并排序函数。
3. 将两个有序的子数组进行合并，得到一个有序的数组。合并过程中，从两个子数组的第一个元素开始，依次比较大小，将较小的元素放入新的数组中。
4. 将合并得到的有序数组返回。

归并排序的关键在于合并两个有序的子数组，这一步可以使用辅助数组来存储合并的结果。合并时，可以使用两个指针分别指向两个子数组的起始位置，比较指针指向的元素的大小，将较小的元素放入新的数组中，并将对应指针后移一位。当一个子数组遍历完后，将另一个子数组剩余的元素直接放入新的数组中即可。

1.2 递归实现

非递归实现归并排序的思想是通过迭代和循环来分割和合并数组，而不使用递归。

1. 初始化一个辅助数组，用于存储合并的结果。
2. 从数组的起始位置开始，将数组中的每个元素看作一个独立的有序序列，将它们分别放入辅助数组。
3. 设置一个变量gap，初始值为1，代表每次合并的有序子序列的长度。
4. 进入循环，循环条件是gap小于数组的长度。
5. 在每一次循环中，将两个有序子序列合并并放入辅助数组中。
6. 将合并得到的有序子序列放回原数组的对应位置。
7. 将gap的值加倍，继续下一轮循环，直到gap大于或等于数组的长度

通过不断合并较小的有序子序列，直到整个数组排序完成，即可得到最终的有序数组。非递归实现归并排序的好处是减少了函数调用的开销，提高了排序的效率。

void _MergeSort(int* a, int begin, int end, int* tmp)
{
	if (begin >= end)
	{
		return;
	}
	int mid = (begin + end) / 2;
	_MergeSort(a, begin, mid, tmp);
	_MergeSort(a, mid + 1, end, tmp);

	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1, end2 = end;
	int i = begin;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}

	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}

	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}

	memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}
	_MergeSort(a, 0, n - 1, tmp);
	free(tmp);
}

1.3 非递归实现

//非递归
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}

	int gap = 1;
	while (gap < n)
	{
		//printf("gap:%2d->", gap);
		for (size_t i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			// [begin1, end1][begin2, end2] 归并

			// 边界的处理
			if (end1 >= n || begin2 >= n)
			{
				break;
			}

			if (end2 >= n)
			{
				end2 = n - 1;
			}

			int j = begin1;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}

			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}

			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}

			memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
		}

		//printf("\n");

		gap *= 2;
	}


	free(tmp);
}

2. 计数排序

2.1 基本思想

计数排序是一种线性时间复杂度的排序算法，适用于一定范围内的整数排序。其基本思想是通过统计每个元素的出现次数，然后根据统计结果将元素放置到正确的位置上。

1. 统计每个元素出现的次数，创建一个计数数组，并初始化为0。
2. 遍历待排序的数组，将每个元素对应的计数数组的对应位置加1，即统计元素出现次数。
3. 对计数数组进行顺序累加，得到每个元素在排序后的数组中的最后一个下标位置。
4. 创建一个临时数组，长度与待排序数组相同。
5. 遍历待排序数组，根据元素值在计数数组中的累加结果，将元素放置到临时数组中的对应位置上。
6. 将临时数组复制回原始数组，完成排序。

需要注意的是，计数排序只适用于非负整数排序，并且在k不是很大的情况下才能保证排序的效率。

2.2 代码实现

//计数排序
void CountSort(int* a, int n)
{
	int min = a[0], max = a[0];
	for (int i = 1; i < n; i++)
	{
		if (a[i] < min)
			min = a[i];

		if (a[i] > max)
			max = a[i];
	}

	int range = max - min + 1;
	int* count = (int*)calloc(range, sizeof(int));
	if (count == NULL)
	{
		printf("calloc fail\n");
		return;
	}

	// 统计次数
	for (int i = 0; i < n; i++)
	{
		count[a[i] - min]++;
	}

	// 排序
	int i = 0;
	for (int j = 0; j < range; j++)
	{
		while (count[j]--)
		{
			a[i++] = j + min;
		}
	}
}