什么是线段树？

线段树是用于储存区间信息的数据结构。

线段树将区间划分为左右子区间进行递归求解，便形成了树形结构。并通过合并两区间信息从而取得任意区间信息

例如对于数组a={10, 11, 12, 13, 14}，那么就可以构建以下线段树

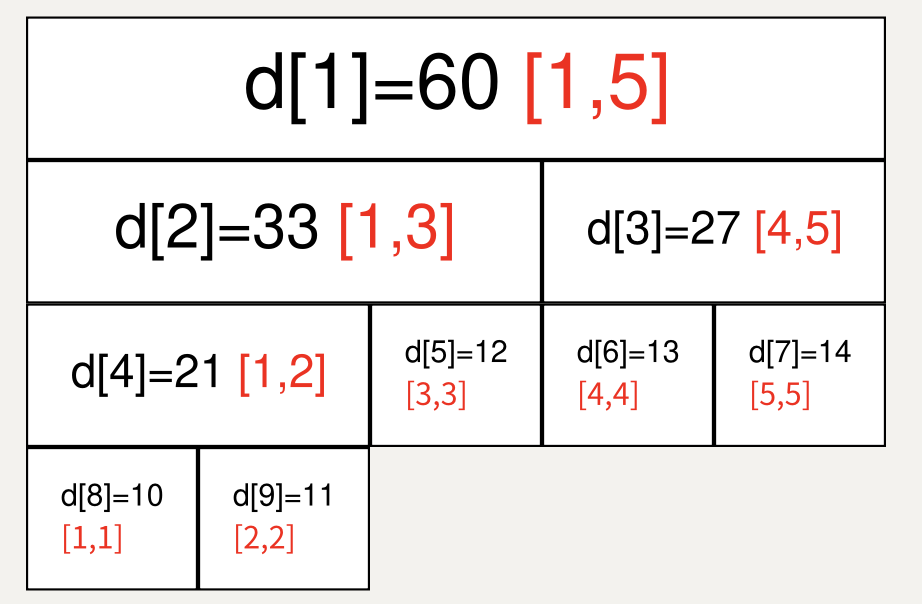
构建

以数组作为线段树的基本结构，储存信息

type SegmentTree struct {
	// 原数组
	arr []int
	// 线段树
	st []int
	// 懒惰标记。延迟对节点修改，在访问时才进行修改
	lazyMark []int
}

func NewSegmentTree(arr []int) *SegmentTree {
	if len(arr) == 0 {
		return nil
	}

	segTree := SegmentTree{
		arr:      arr,
		st:       make([]int, 4*len(arr)),
		lazyMark: make([]int, 4*len(arr)),
	}

	for i := range segTree.lazyMark {
		//fill LazyTree with empty lazy nodes
		segTree.lazyMark[i] = emptyLazyNode
	}

	//starts with node 1 and interval [0, len(arr)-1] inclusive
	segTree.Build(1, 0, len(arr)-1)

	return &segTree
}

func (s *SegmentTree) Build(node int, left, right int) {
	// 当左右边界相等时，线段节点就是数组节点
	if left == right {
		s.st[node] = s.arr[left]
		return
	}

	// 将数组分为两部分进行构建
	mid := (left + right) / 2

	s.Build(2*node, left, mid)
	s.Build(2*node, mid+1, right)

	s.st[node] = s.st[2*node] + s.st[2*node+1]
}

区间查询

区间查询是通过组合多个子区间合并信息来实现的

// left、right指向节点区间
// ql、qr指向查询区间
func (s *SegmentTree) Query(node int, left, right int, ql, qr int) int {
	// 无效值直接返回
	if (ql > qr) || (left > right) {
		return 0
	}

	// 若存在标记，则更新
	s.Propagate(node, left, right)

	// 当前区间为询问区间的子集时直接返回当前区间的和
	if left >= ql && right <= qr {
		return s.st[node]
	}

	// 继续分左右子区间递归查询
	mid := (left + right) / 2
	leftNodeSum := s.Query(2*node, left, mid, ql, minInt(mid, qr))
	rightNodeSum := s.Query(2*node+1, mid+1, right, maxInt(ql, mid+1), qr)

	return leftNodeSum + rightNodeSum
}

func minInt(x, y int) int {
	if x < y {
		return x
	}
	return y
}

func maxInt(x, y int) int {
	if x > y {
		return x
	}
	return y
}

区间修改与懒惰标记

在前文中已经出现了Propagate方法，那么这个方法是做什么的呢？

考虑到如果修改区间会导致包含在该区间内的所有节点都遍历一次，修改一次，那么这会导致时间复杂度非常高，因此引入了懒惰标记。而Propagate方法则是在查询和更新相应节点时更新懒惰标记

懒惰标记，简单来说，就是通过延迟对节点信息的更改，从而减少可能不必要的操作次数。每次执行修改时，我们通过打标记的方法表明该节点对应的区间在某一次操作中被更改，但不更新该节点的子节点的信息。

现在假如说准备给区间[3,5]中每个数都加上3，那么根据区间查询规则，匹配到了[3,3]和[4,5]两个区间，因此直接更新这两个区间的懒惰标记lazyMark=3。

接着查询了[4,4]区间的数字，触发懒惰更新，使得[4,5]信息更新，并将标记下方到其子区间

func (s *SegmentTree) Update(node int, left, right int, ql, qr int, val int) {
	// 触发懒惰标记更新
	s.Propagate(node, left, right)

	// 无效值返回
	if ql > qr || left > right {
		return
	}

	if left >= ql && right <= qr {
		// 当前区间为查询区间的子区间，则更新懒惰标记，并传递更新
		s.lazyMark[node] += val
		s.Propagate(node, left, right)
	} else {
		// 分左右子区间递归更新
		mid := (left + right) / 2

		s.Update(2*node, left, mid, ql, minInt(mid, qr), val)
		s.Update(2*node+1, mid+1, right, maxInt(ql, mid+1), qr, val)

		s.st[node] = s.st[2*node] + s.st[2*node+1]
	}
}

func (s *SegmentTree) Propagate(node, left, right int) {
	// 如果存在标记
	if s.lazyMark[node] != emptyLazyNode {
		s.st[node] += (right - left + 1) * s.lazyMark[node]

		if left == right {
			// 被标记的是叶节点，那么直接更新
			s.arr[left] += s.lazyMark[node]
		} else {
			// 其他情况下，更新左右子线段节点的标记
			s.lazyMark[2*node] += s.lazyMark[node]
			s.lazyMark[2*node+1] += s.lazyMark[node]
		}

		s.lazyMark[node] = emptyLazyNode
	}
}

Ref

1. https://oi-wiki.org/ds/seg/
2. https://github.com/dougwatson/Go/blob/master/structure/segmenttree/segmenttree.go