代码随想录刷题题Day23

刷题的第二十三天，希望自己能够不断坚持下去，迎来蜕变。😀😀😀
刷题语言：C++
Day23 任务
● 93.复原IP地址
● 78.子集
● 90.子集II

1 复原IP地址

93.复原IP地址

思路：

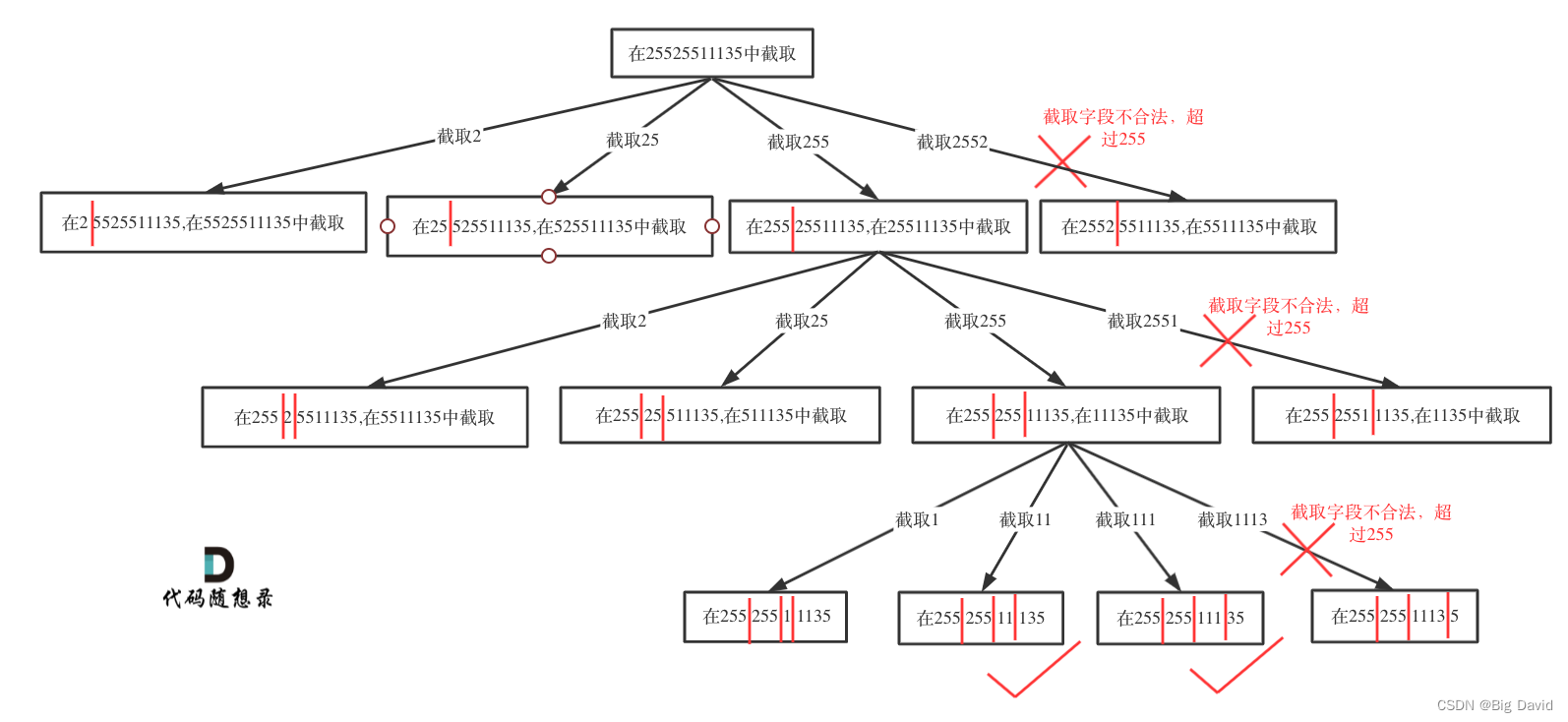
回溯
（1）递归参数
参数：字符串s、startIndex、pointNum

vector<string> result;
// startIndex: 搜索的起始位置，pointNum:添加逗点的数量
void backtracking(string& s, int startIndex, int pointNum)

（2）递归终止条件

本题明确要求只会分成4段，所以不能用切割线切到最后作为终止条件，而是分割的段数作为终止条件

if (pointNum == 3) {
	if (isValid(s, startIndex, s.size() - 1) result.push_back(s);
	return;
}

（3）单层搜索的逻辑

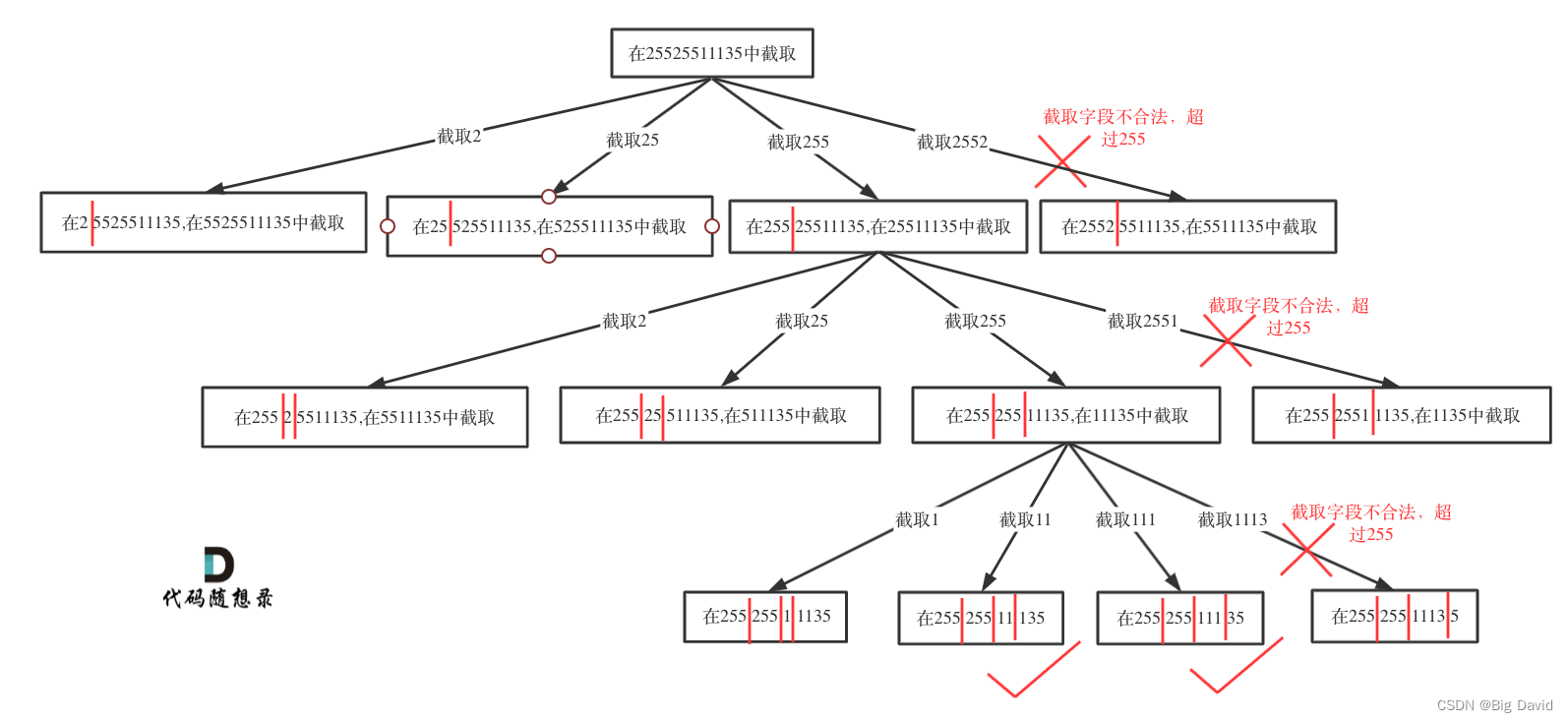
for (int i = startIndex; i < s.size(); i++) {
	if (isValid(s, startIndex, i)) {// 判断 [startIndex,i] 这个区间的子串是否合法
		s.insert(s.begin() + i + 1, '.');// 在i的后面插入一个逗点
		pointNum++;
		backtracking(s, i + 2, pointNum);// 插入逗点之后下一个子串的起始位置为i+2
		pointNum--;// 回溯
		s.erase(s.begin() + i + 1);// 回溯
	} else break;
}

判断子串是否合法：
（1）以0为开头的数字不合法
（2）有非正整数字符不合法
（3）如果大于255了不合法

bool isValid(const string& s, int start, int end) {
	if (start > end) return false;
	if (s[start] == '0' && start != end) return false;
	int num = 0;
	for (int i = start; i <= end; i++) {
		if (s[i] > '9' || s[i] < '0') return false;
		num = num * 10 + (s[i] - '0');
		if (num > 255) return false;
	}
	return true;
}

C++：

class Solution {
public:
	vector<string> result;// 记录结果
	// startIndex: 搜索的起始位置，pointNum:添加逗点的数量
	void backtracking(string& s, int startIndex, int pointNum) {
		if (pointNum == 3) {// 逗点数量为3时，分隔结束
			if (isValid(s, startIndex, s.size() - 1))
			    result.push_back(s);
		    return;
		}
		for (int i = startIndex; i < s.size(); i++) {
			if (isValid(s, startIndex, i)) {// 判断 [startIndex,i] 这个区间的子串是否合法
				s.insert(s.begin() + i + 1, '.');// 在i的后面插入一个逗点
				pointNum++;
				backtracking(s, i + 2, pointNum);// 插入逗点之后下一个子串的起始位置为i+2
				pointNum--;// 回溯
				s.erase(s.begin() + i + 1);// 回溯
			} else break;
		}
	}
	// 判断字符串s在左闭又闭区间[start, end]所组成的数字是否合法
	bool isValid(const string& s, int start, int end) {
		if (start > end) return false;
		if (s[start] == '0' && start != end) {// 0开头的数字不合法
			return false;
		}
		int num = 0;
		for (int i = start; i <= end; i++) {
			if (s[i] > '9' || s[i] < '0') return false;// 遇到非数字字符不合法
			num = num * 10 + s[i] - '0';
			if (num > 255) return false; // 如果大于255了不合法
		}
		return true;
	}
    vector<string> restoreIpAddresses(string s) {
		if (s.size() < 4 || s.size() > 12) return result;
		backtracking(s, 0, 0);
		return result;
    }
};

时间复杂度：$O(3^4)$
空间复杂度：$O(n)$

2 子集

78.子集

思路：
组合问题和分割问题都是收集树的叶子节点，而子集问题是找树的所有节点

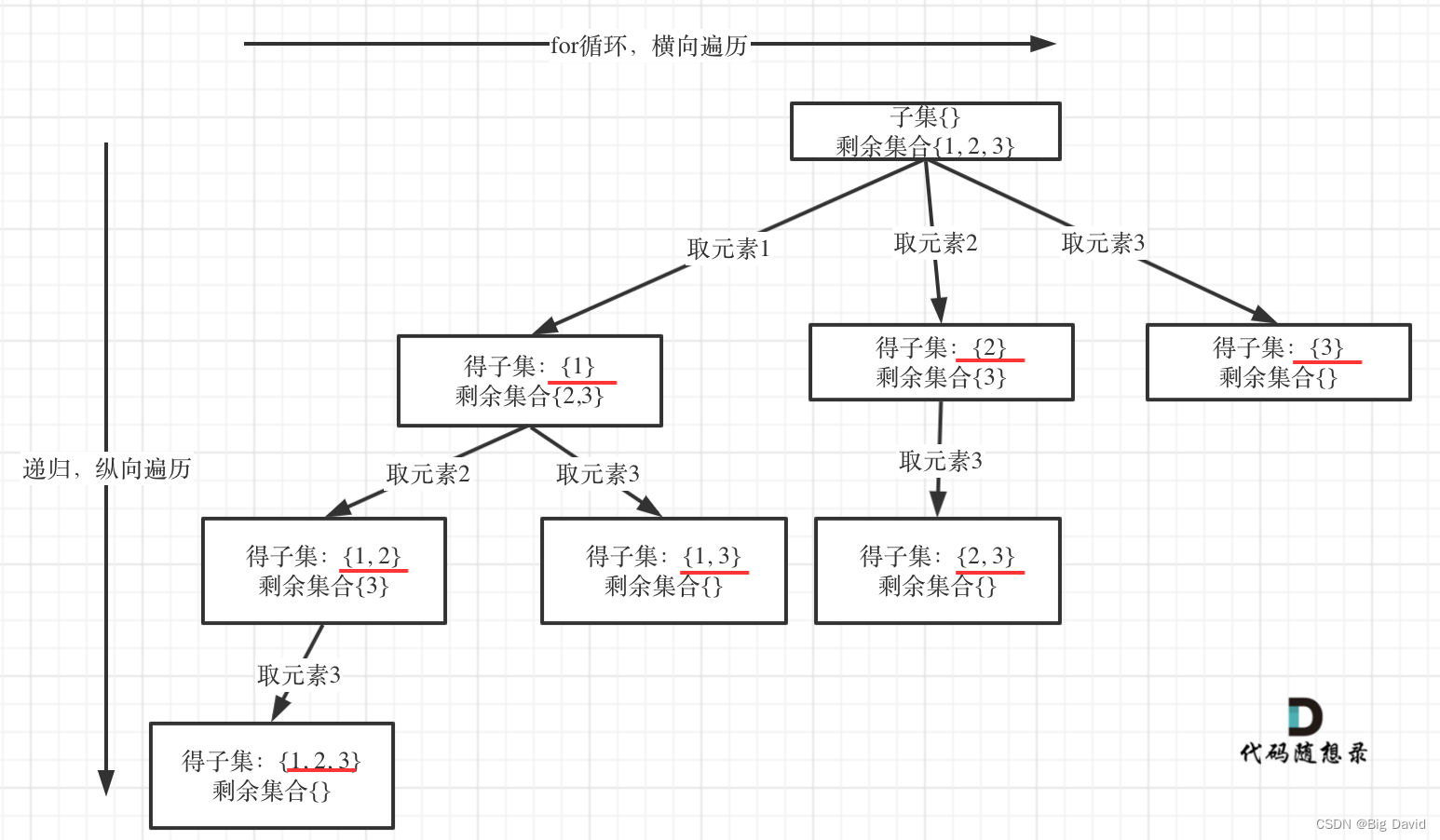
（1）递归函数参数

vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums, int startIndex)

（2）递归终止条件

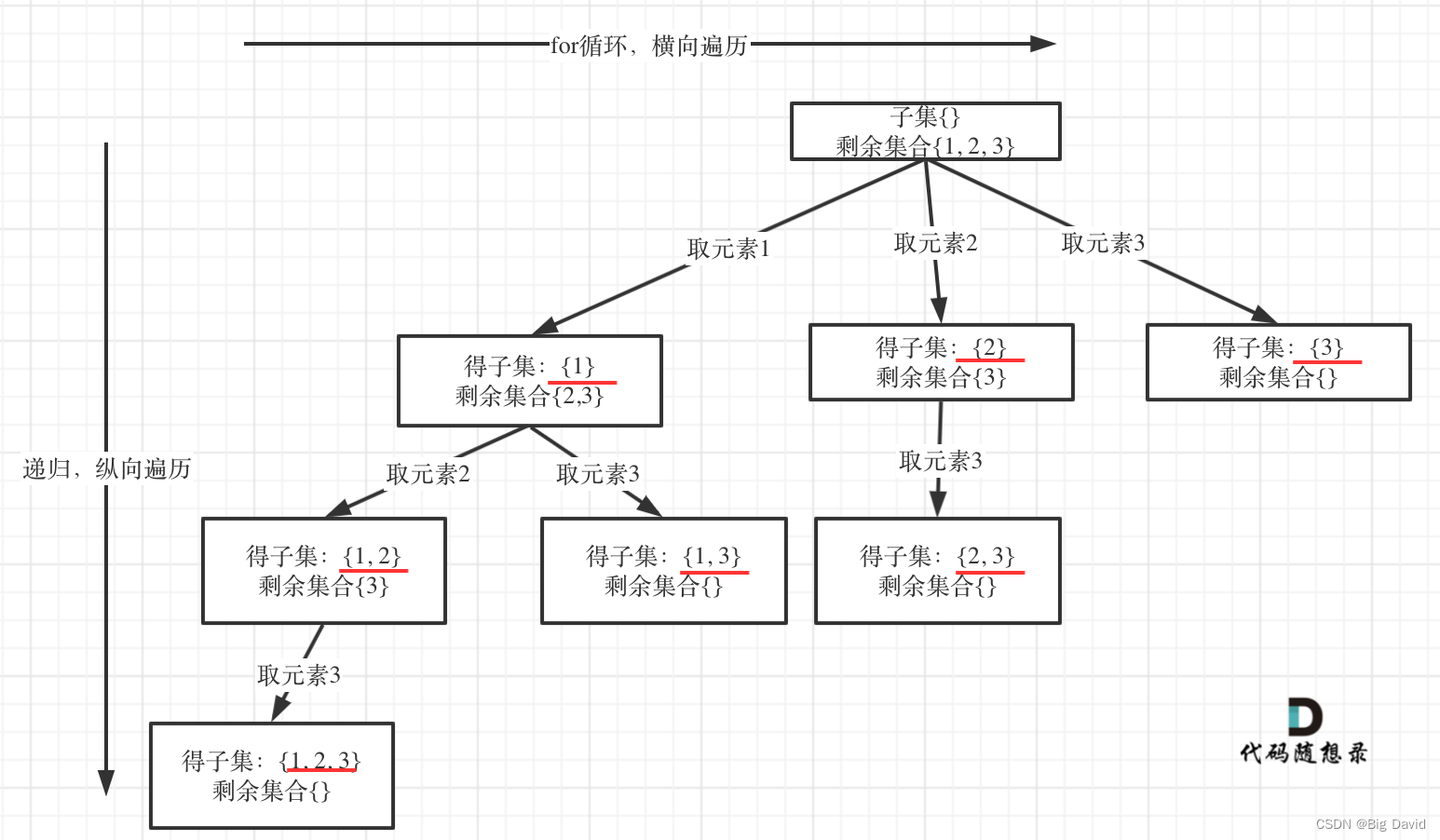
剩余集合为空的时候，就是叶子节点

if (startIndex >= nums.size()) return;

（3）单层搜索逻辑

求取子集问题，不需要任何剪枝！因为子集就是要遍历整棵树

for (int i = startIndex; i < nums.size(); i++) {
	path.push_back(nums[i]);// 子集收集元素
	backtracking(nums, i + 1);// 注意从i+1开始，元素不重复取
	path.pop_back();// 回溯
}

C++：

class Solution {
public:
    vector<int> path;
    vector<vector<int>> result;
    void backtracking(vector<int>& nums, int startIndex) {
        result.push_back(path);// 收集子集，要放在终止添加的上面
        if (startIndex >= nums.size()) return;
        for (int i = startIndex; i < nums.size(); i++) {
            path.push_back(nums[i]);
            backtracking(nums, i + 1);
            path.pop_back();
        }
    }
    vector<vector<int>> subsets(vector<int>& nums) {
        backtracking(nums, 0);
        return result;
    }
};

时间复杂度: $O(n?2^n)$
空间复杂度: $O(n)$

（1）子集是收集树形结构中树的所有节点的结果
（2）组合问题、分割问题是收集树形结构中叶子节点的结果

3 子集II

90.子集II

思路：

和前一个题目的区别就是集合里有重复元素，而且求取的子集要去重。

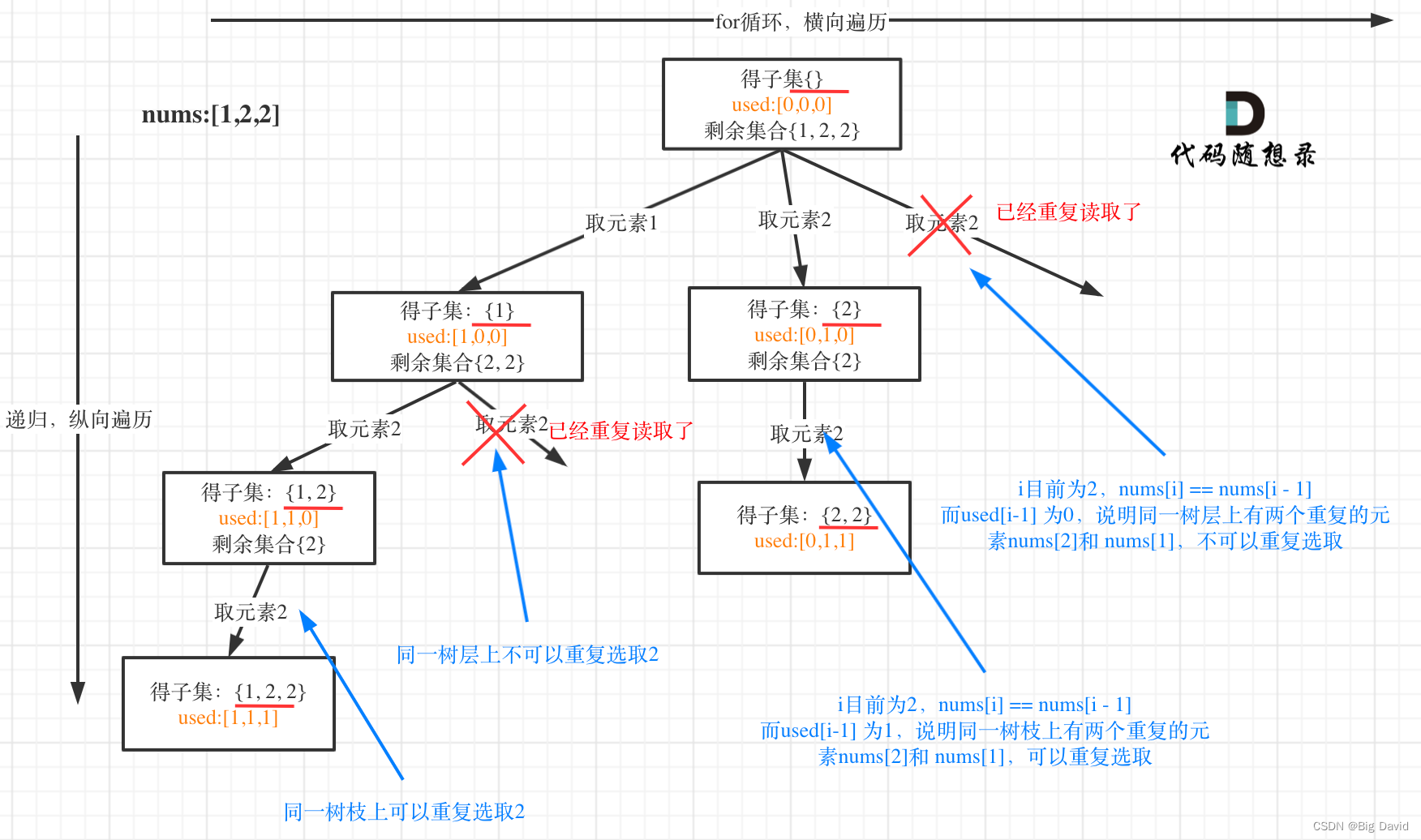
同一树层上重复取2 就要过滤掉，同一树枝上就可以重复取2，因为同一树枝上元素的集合才是唯一子集

class Solution {
public:
    vector<int> path;
    vector<vector<int>> result;
    void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
        result.push_back(path);
        if (startIndex >= nums.size()) {
            return;
        }
        for (int i = startIndex; i < nums.size(); i++) {
        	// used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
            // used[i - 1] == false，说明同一树层candidates[i - 1]使用过
            // 而我们要对同一树层使用过的元素进行跳过
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) continue;
            path.push_back(nums[i]);
            used[i] = true;
            backtracking(nums, i + 1, used);
            used[i] = false;
            path.pop_back();
        }
    }
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        vector<bool> used(nums.size(), false);
        sort(nums.begin(), nums.end());// 去重需要排序
        backtracking(nums, 0, used);
        return result;
    }
};

时间复杂度: $O(n?2^n)$
空间复杂度: $O(n)$

---

鼓励坚持二十四天的自己😀😀😀