运筹优化 | 模拟退火求解旅行商问题 | Python实现
发布时间:2023年12月18日
"""模拟退火旅行商"""
import random
import numpy as np
import math
import time
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
location = np.loadtxt('city_location.txt') # 加载数据
'''一些关键参数'''
num_city = 30 # 城市总数
initial_t = 100 # 初始温度
lowest_t = 0.001 # 最低温度
iteration = 10000 # 设置迭代次数
'''输入两个城市之间的距离'''
def distance_mat():
distance = [] # 初始化距离数组
for i in range(30):
distance_each = [] # 初始化每个城市到其他城市的距离
for j in range(30):
dis = math.sqrt(pow(location[i][0] - location[j][0], 2) +
pow(location[i][1] - location[j][1], 2)) # 计算距离
distance_each.append(dis) # 赋值到distance_each数组
distance.append(distance_each) # 按列添加
return distance
'''计算所有路径对应的距离'''
def cal_newpath(distance, path):
# 此时传入的path是一条随机生成的路径
dis = 0
for j in range(num_city - 1): # 只遍历0到28个城市,是因为第29个城市的下一个是起点,这样才是TSP问题,形成闭环
dis = distance[path[j]][path[j + 1]] + dis # 这条路径上经过的两两个点的距离之和即为这条路径的长度
dis = dis + distance[path[29]][path[0]] # 计算的距离之和再加上第28个城市回到起点的距离
return dis
'''点对点的距离矩阵'''
distance = distance_mat()
'''初始路径'''
path = list(range(30)) # 生成0到29的列表,即城市索引
'''初始距离'''
dis = cal_newpath(distance, path) # 先计算初始的距离,这样在模拟退火的时候才可以开始比较
'''初始温度'''
t_current = initial_t
'''灵敏度分析'''
sensibility = []
start_time = time.time() # 开始计时
'''模拟退火'''
while t_current > lowest_t: # 外层循环:改变温度
count_m = 0 # M的计数
count_iter = 0 # 迭代次数计数
while count_iter < iteration: # 内层循环:连续多次不接受新的状态则跳出内循环
i = 0
j = 0
while i == j: # 防止随机了同一城市
i = random.randint(1, 29)
j = random.randint(1, 29)
path_new = path.copy()
path_new[i], path_new[j] = path_new[j], path_new[i] # 任意交换两个城市的位置,产生新的路径组合
dis_new = cal_newpath(distance, path_new) # 计算新路径的距离
dis_delta = dis_new - dis # 计算新距离和旧距离的差值
rand = random.random() # 生成一个0到1的浮点随机数
exp_d = math.exp(-dis_delta / t_current) # Metropolis准则
'''是否接受新解的过程'''
if dis_delta < 0: # 如果新距离小于旧距离,则直接接受
path = path_new
dis = dis_new
elif exp_d > rand: # 如果新距离大于旧距离,用Metropolis准则判断是否接受
path = path_new
dis = dis_new
else: # 不接受新解
count_m = count_m + 1
count_iter = count_iter + 1 # 迭代次数加1
sensibility.append(dis)
t_current = 0.99 * t_current # 改变温度
end_time = time.time()
elapsed_time = end_time - start_time
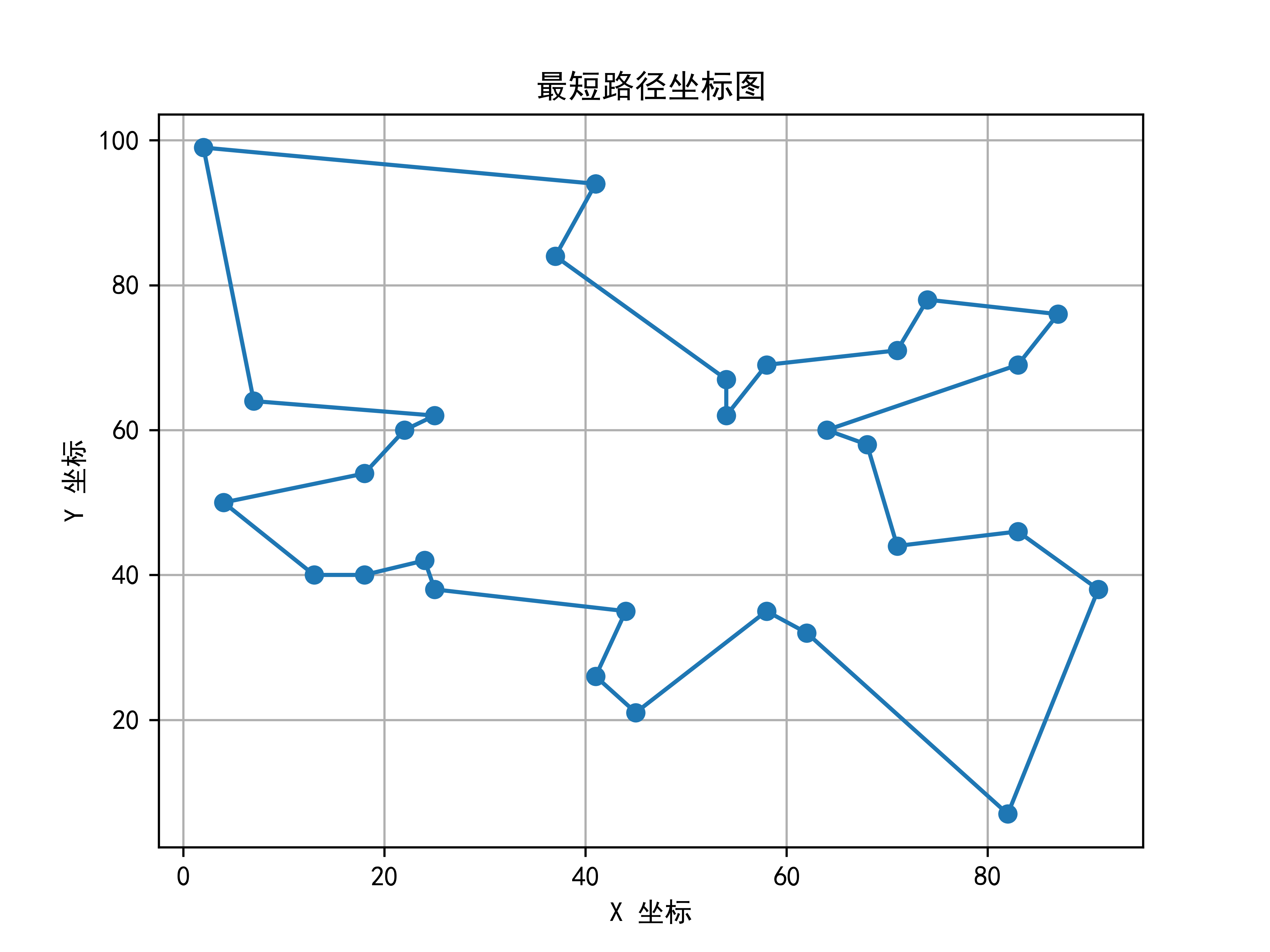
# 绘制最短路径的坐标图
x_coords = [location[i][0] for i in path]
y_coords = [location[i][1] for i in path]
# 添加起点到终点的连线
x_coords.append(x_coords[0])
y_coords.append(y_coords[0])
plt.figure(1)
plt.plot(x_coords, y_coords, marker='o', linestyle='-')
plt.title('最短路径坐标图')
plt.xlabel('X 坐标')
plt.ylabel('Y 坐标')
plt.grid(True)
plt.show()
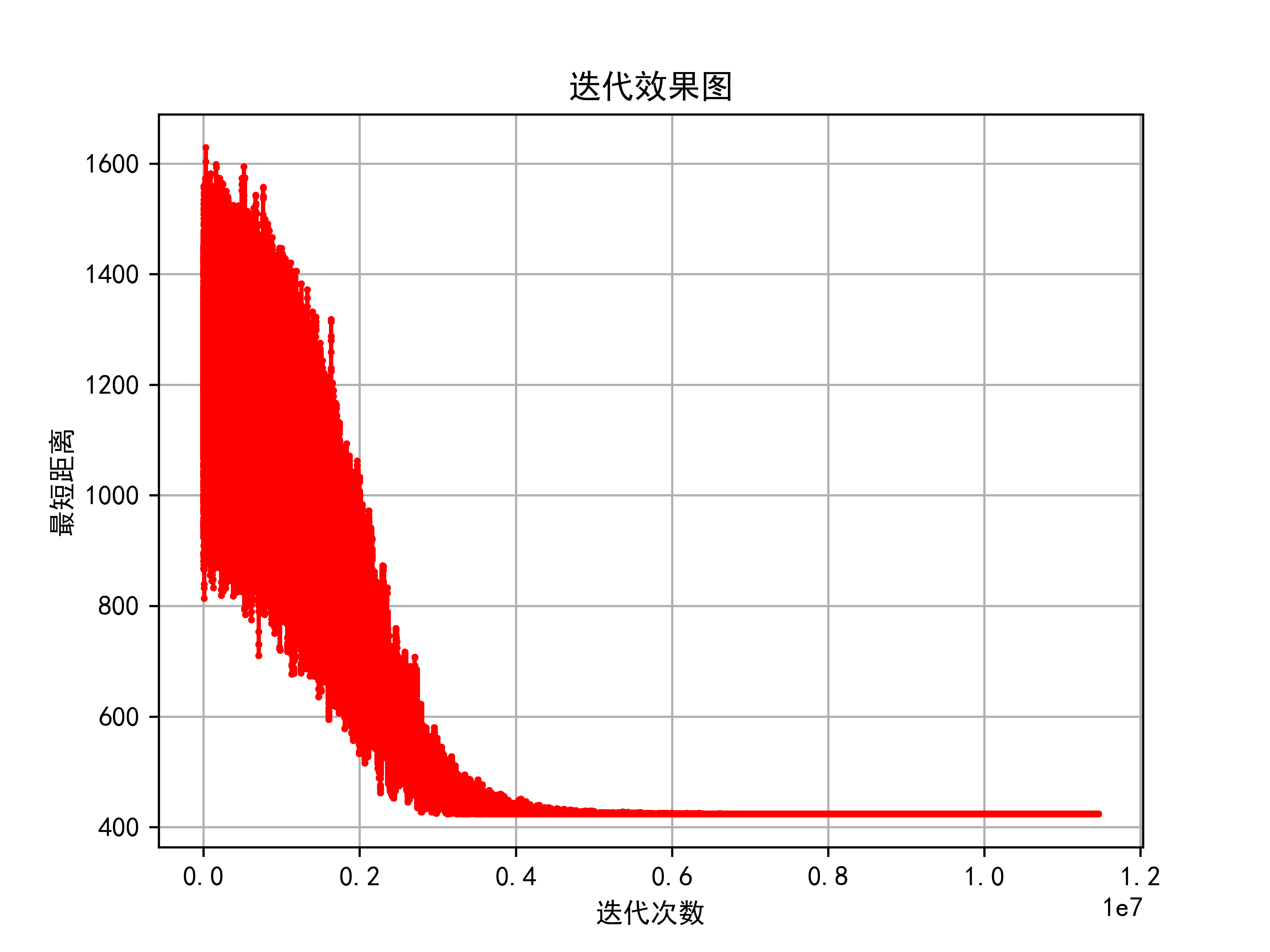
plt.figure(2)
plt.plot(sensibility,marker='.',color='r',markersize=3)
plt.title('最短路径坐标图')
plt.xlabel('迭代次数')
plt.ylabel('最短距离')
plt.grid(True)
plt.show()
'''输出结果'''
print('最短距离:', dis)
print('最短路径:', path)
print('运行时间:', elapsed_time, '秒')最短距离: 424.69177537685437
最短路径: [0, 5, 4, 3, 12, 11, 29, 22, 21, 16, 15, 28, 27, 26, 25, 24, 23, 14, 13, 7, 9, 20, 19, 18, 6, 10, 8, 2, 17, 1]
运行时间: 43.86513066291809 秒
文章来源:https://blog.csdn.net/L040514/article/details/134983713
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- x-cmd-mod | zuz - 压缩或解压文件
- BL120AC 工业空调网关 空调协议转Modbus协议网关
- 使用Flink处理Kafka中的数据
- 利用python批量压缩图教程:如何轻松减小图片大小
- Vue-API
- 044、门控
- 基于YOLOv8深度学习的吸烟/抽烟行为检测系统【python源码+Pyqt5界面+数据集+训练代码】目标检测、深度学习实战
- Java技术-isEmpty 和 isBlank 的用法区别
- python 学习笔记1
- SSM房屋租赁系统----计算机毕业设计