数据结构：直接选择排序和堆排序

?直接选择排序：

这里我用两个变量同时找出最小值和最大值。

注意：若begin为最大值，maxi即为最大值的下标，若将最小值与其交换，最大值的下标此时就不再是maxi，而变为mini了，故此时要调整maxi的位置

直接选择排序的时间复杂度 O(N^2)

void PrintArray(int* a, int n)
{
	int i;
	for (i = 0; i < n; i++)
	{
		printf("%d ", *(a + i));
	}
}
void Swap(int* a, int* b)
{
	int tem = *a;
	*a = *b;
	*b = tem;
}
//直接选择排序
void SelectedSort(int* a, int n)
{
	int begin = 0, end = n - 1;
	while (begin < end)
	{
		int mini = begin, maxi = end;
		for (int i = begin; i <= end; i++)
		{
			if (a[i] < a[mini])
				mini = i;
			if (a[i] > a[maxi])
				maxi = i;
		}
		Swap(&a[begin], &a[mini]);
		//如果begin与maxi重叠，需要修正maxi此时max被换到了mini的位置上
		if (begin == maxi)
			maxi = mini;
		Swap(&a[maxi], &a[end]);
		begin++;
		end--;
	}
}
void TestSelectedSort()
{
	int a[] = { 3,5,2,7,8,6,1,9,4,0 };
	SelectedSort(a, sizeof(a) / sizeof(int));
	PrintArray(a, sizeof(a) / sizeof(int));
}

堆排序：?

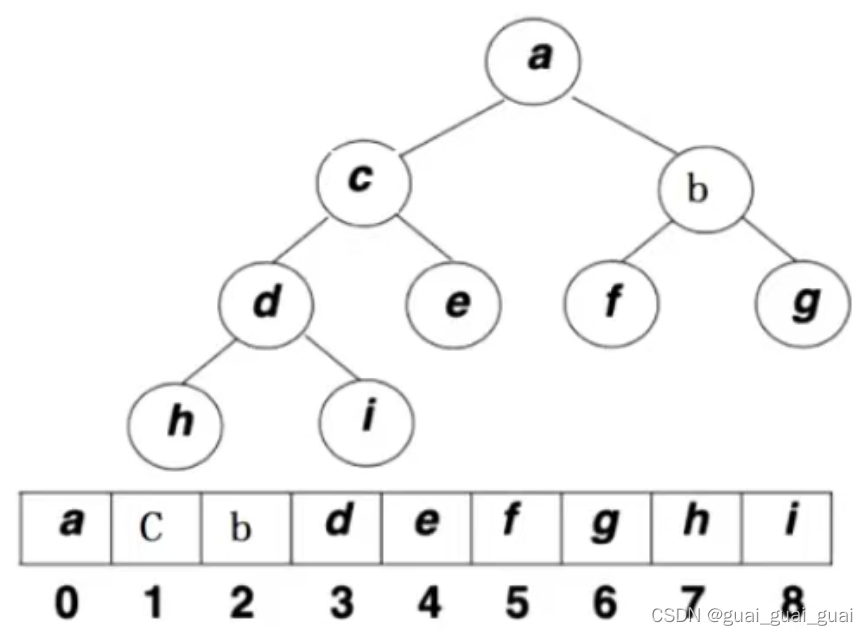
• 堆的逻辑结构是一颗完全二叉树
• 堆的物理结构是一个数组

数组下标的父子节点关系

leftchild=parent*2+1

rightchild=parent*2+2

parent=(child-1)/2

堆的两个特性：

• 结构性：用数组表示的完全二叉树
• 有序性：任一节点的节点的关键字是其子树所有结点的最大值或最小值
• “最大堆（MaxHeap）”，也称“大顶堆”：最大值
• “最小堆（MinHeap）”，也称“小顶堆”：最小值
• 大堆要求：树中所有的父亲都大于等于孩子，堆顶的数据是最大的
• 小堆要求：树中所有的父亲都小于等于孩子，堆顶的数据是最小的

建小堆

向下调整算法

前提：左右子树都是小堆

从根节点开始选出左右孩子中小的那一个，跟父亲比较，如果比父亲小就交换，然后再继续往下调

建堆的时间复杂度为O(N)。

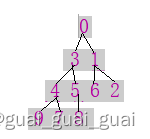
如果左右子树不是小堆，该怎么建小堆呢？

我们可以倒着从最后一棵子树开始调，倒着走，从倒数第一个非叶子的子树开始调，即为从8开始，那如何找到8呢，只需找出最后一个数据的下标利用父子节点的关系求出即可，即（n-1）-1/2.

若是升序，应该建大堆还是小堆呢？我第一次认为是小堆，实则不然，若是小堆，小堆会把最小的数放在第一位，选择排序是通过堆来选树，最小数此时在堆顶已被选出，此时就要在剩下的树里选树，但此时新树的结构就已经乱了，之前所建的小堆已经不复存在，需要再建小堆才能选出下一个树，建堆的时间复杂度为O（N），这样建堆所带来的效率优势就没了。故升序不能建小堆

正确的应该是建大堆，将第一个数和最后一个数交换，此时最后一个数为最大的数，不把它看成是堆里面的数，前n-1个数向下调整，选出次大的数，再跟倒数第二个位置交换，以此类推，此时中间堆的结构未改变。

堆排序的时间的复杂度为O(N*logN)?

堆排序代码如下：

//堆排序
//建大堆
void Swap(int*a, int*b)
{
	int tem = *a;
	*a = *b;
	*b = tem;
}
//向下调整算法
void AdjustDown(int* a, int n, int root)
{
	int parent = root;
	int child = parent * 2 + 1;//默认是左孩子
	while (child<n)
	{
		//1.选出左右孩子中最大的一个
		if (child+1<n&&a[child + 1] > a[child])//防止数组越界，所以要加child+1<n
		{
			child++;
		}
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
        //若孩子本来就比父亲小，因为大堆的每棵树都是大堆，说明此时堆已经建好，break即可
		else
			break;
	}
}
void HeapSort(int* a, int n)
{
	//把数组建成堆 倒着走
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)//n-1为最后一个元素的下标，(n-1-1)/2即为parent
	{
		AdjustDown(a, n, i);
	}
	//排升序，建大堆
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
	}
}
void PrintArray(int* a, int n)
{
	int i;
	for (i = 0; i < n; i++)
	{
		printf("%d ", *(a + i));
	}
}
void TestHeapSort()
{
	int a[] = { 3,5,2,7,8,6,1,9,4,0 };
	HeapSort(a, sizeof(a) / sizeof(int));
	PrintArray(a, sizeof(a) / sizeof(int));
}

int main()
{
	TestHeapSort();
	return 0;
}