数据结构：图的存储和遍历

图也是一种数据结构，在实际生活中有广泛运用，因此本篇总结的就是图的存储等

图的存储结构

在图中既有节点，也有边，因此要存储的就是节点和边的关系，节点的存储只需要放在一个数组中就可以，那边的存储是如何进行存储的？

邻接矩阵

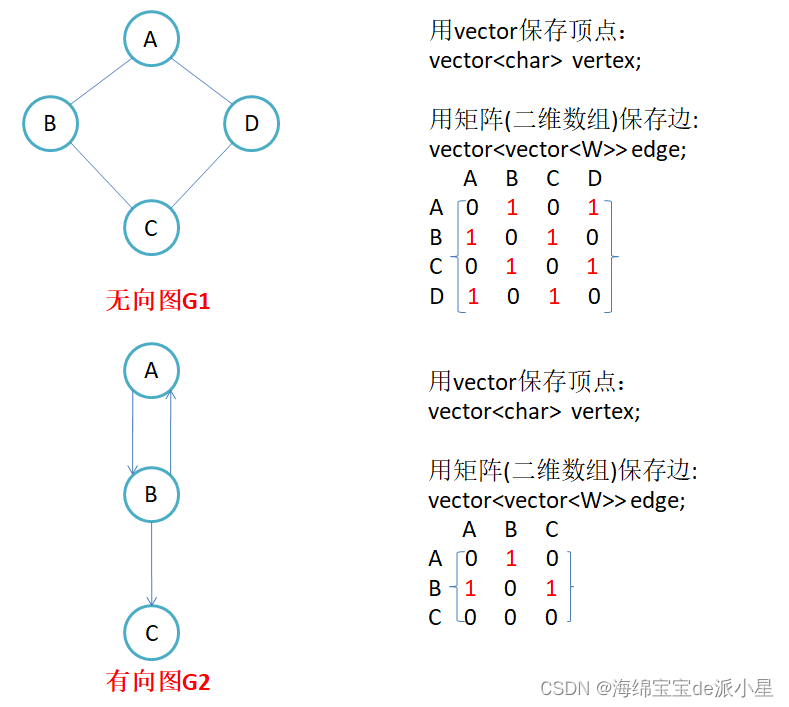
利用一个二维数组来存储，对于任意一个不越界的下标i和j来说，arr[i][j]表示的是i和j这两个点之间的关系，如果是0表示的是从i到j没有关系，如果是1表示的是它们之间存在边

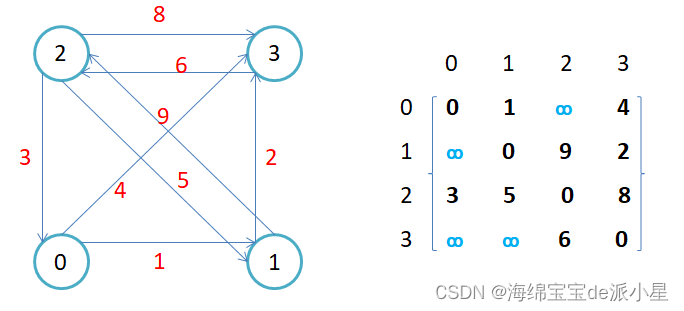
如果这个这个图是带有权值的，那么边的关系就使用权值来代替，如果顶点之间没有关系，就用无穷来表示即可

缺点

用邻接矩阵存储图的有点是能够快速知道两个顶点是否连通，缺陷是如果顶点比较多，边比较少时，矩阵中存储了大量的0成为系数矩阵，比较浪费空间，并且要求两个节点之间的路径不是很好求

邻接矩阵的存储模拟实现

// 顶点的类型，权值的类型，权值的最大值，是否是有向图
template<class V, class W, W W_MAX = INT_MAX, bool Direction = false>
class Graph
{
public:
	Graph(const V* vertexs, size_t n)
	{
		// 建立顶点和下标的映射关系
		for (size_t i = 0; i < n; i++)
		{
			_vertexs.push_back(vertexs[i]);
			_vIndexMap[vertexs[i]] = i;
		}

		_matrix.resize(n, vector<W>(n, W_MAX));
	}

	// 给一个顶点取出来它对应的下标
	size_t GetVertexsIndex(const V& vertex)
	{
		auto it = _vIndexMap.find(vertex);
		if (it != _vIndexMap.end())
		{
			return it->second;
		}
		else
		{
			throw invalid_argument("不存在的顶点");
			return -1;
		}
	}

	// 给邻接矩阵加值
	void _AddEdge(size_t srci, size_t dsti, W w)
	{
		_matrix[srci][dsti] = w;
		if (Direction == false)
			_matrix[dsti][srci] = w;
	}

	// 加边
	void AddEdge(const V& src, const V& dst, W w)
	{
		size_t srci = GetVertexsIndex(src);
		size_t dsti = GetVertexsIndex(dst);
		_AddEdge(srci, dsti, w);
	}

	// 显示邻接矩阵
	void Print()
	{
		// 打印顶点和下标映射关系
		for (size_t i = 0; i < _vertexs.size(); ++i)
		{
			cout << _vertexs[i] << "-" << i << " ";
		}
		cout << endl << endl;
		cout << "  ";
		for (size_t i = 0; i < _vertexs.size(); ++i)
		{
			cout << i << " ";
		}
		cout << endl;
		// 打印矩阵
		for (size_t i = 0; i < _matrix.size(); ++i)
		{
			cout << i << " ";
			for (size_t j = 0; j < _matrix[i].size(); ++j)
			{
				if (_matrix[i][j] != W_MAX)
					cout << _matrix[i][j] << " ";
				else
					cout << "#" << " ";
			}
			cout << endl;
		}
		cout << endl << endl;
		// 打印所有的边
		for (size_t i = 0; i < _matrix.size(); ++i)
		{
			for (size_t j = 0; j < _matrix[i].size(); ++j)
			{
				if (i < j && _matrix[i][j] != W_MAX)
				{
					cout << _vertexs[i] << "-" << _vertexs[j] << ":" <<
						_matrix[i][j] << endl;
				}
			}
		}
	}
private:
	// 下标到顶点的映射
	vector<V> _vertexs;
	// 邻接矩阵的存储
	vector<vector<W>> _matrix;
	// 顶点到下标的映射
	map<V, size_t> _vIndexMap;
};

整体来说难度并不大，只是单纯的进行存储，注意map的使用是为了让顶点和下标建立一层映射，便于快速根据顶点可以定位到下标

邻接表

邻接表是另外一种图的存储形式，它适用于稀疏图，主要是借助链表来表示边和边的关系

无向图的存储

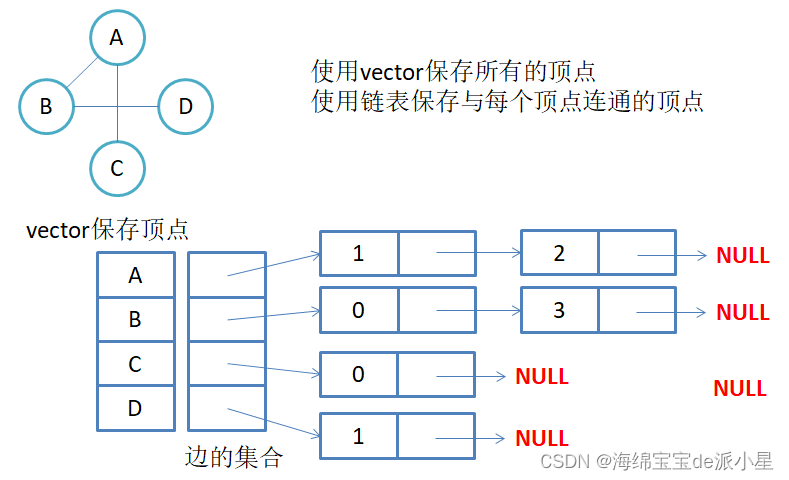
邻接表的好处也就体现出来了，想要知道A点和哪个点相连，遍历一下A所在的链表就可以知道了，而不需要在邻接矩阵中从头到尾进行遍历一次

有向图的存储

有了基本的原理支持，下面开始进行邻接表的模拟实现

邻接表的模拟实现

namespace list_table
{
	// 对于边的结构来说，需要存储的有边的两个顶点，边的权值，以及链接属性
	template <class W>
	struct Edge
	{
		Edge() = default;
		Edge(size_t srci, size_t dsti, W w)
			:_srci(srci)
			, _dsti(dsti)
			, _w(w)
			, _next(nullptr)
		{}
		size_t _srci;
		size_t _dsti;
		W _w;
		Edge<W>* _next;
	};

	// 顶点的类型，权值的类型，权值的最大值，是否是有向图
	template<class V, class W, bool Direction = false>
	class Graph
	{
		typedef Edge<W> Edge;
	public:
		Graph() = default;
		Graph(const V* vertexs, size_t n)
		{
			// 建立顶点和下标的映射关系
			for (size_t i = 0; i < n; i++)
			{
				_vertexs.push_back(vertexs[i]);
				_vIndexMap[vertexs[i]] = i;
			}

			_link_tables.resize(n, nullptr);
		}

		// 给一个顶点取出来它对应的下标
		size_t GetVertexsIndex(const V& vertex)
		{
			auto it = _vIndexMap.find(vertex);
			if (it != _vIndexMap.end())
			{
				return it->second;
			}
			else
			{
				throw invalid_argument("不存在的顶点");
				return -1;
			}
		}

		// 给邻接表加值
		void _AddEdge(size_t srci, size_t dsti, W w)
		{
			// 创建一个边的结构
			Edge* EdgePtr = new Edge(srci, dsti, w);
			Edge* tail = _link_tables[srci];
			while (tail && tail->_next)
				tail = tail->_next;
			// 把这个边的结构头插链入到邻接表
			if (tail == nullptr)
			{
				_link_tables[srci] = EdgePtr;
			}
			else
			{
				tail->_next = EdgePtr;
				tail = tail->_next;
			}
		}

		// 加边
		void AddEdge(const V& src, const V& dst, W w)
		{
			size_t srci = GetVertexsIndex(src);
			size_t dsti = GetVertexsIndex(dst);
			_AddEdge(srci, dsti, w);
			// 如果是无向图，就把对应的边也加到邻接表中
			if (Direction == false)
			{
				_AddEdge(dsti, srci, w);
			}
		}

		// 显示邻接矩阵
		void Print()
		{
			// 打印顶点和下标映射关系
			for (size_t i = 0; i < _vertexs.size(); ++i)
			{
				cout << _vertexs[i] << "-" << i << " ";
			}
			cout << endl;
			cout << endl;
			// 打印邻接表
			for (size_t i = 0; i < _link_tables.size(); ++i)
			{
				cout << i << " ";
				Edge* cur = _link_tables[i];
				while (cur)
				{
					cout << "[" << cur->_srci << "->" << cur->_dsti << "]" << "w->" << cur->_w << " ";
					cur = cur->_next;
				}
				cout << endl;
				cout << endl;
			}
			cout << endl << endl;
		}
	private:
		// 下标到顶点的映射
		vector<V> _vertexs;
		// 邻接表的存储
		vector<Edge*> _link_tables;
		// 顶点到下标的映射
		map<V, size_t> _vIndexMap;
	};
}

图的遍历

图的遍历主要有深度优先和广度优先，关于这两个遍历已经在之前的文章中总结过了，下面直接对这两个方法进行实现，这里是利用邻接矩阵进行遍历

DFS和BFS遍历

		// 图的BFS遍历，从某个顶点开始遍历
		void BFS(const V& Vertex)
		{
			queue<V> qe;
			qe.push(Vertex);
			size_t d = 1;
			vector<bool> visited(_matrix.size(), false);
			while (!qe.empty())
			{
				size_t dsize = qe.size();
				cout << Vertex << "的" << d << "度好友:";
				while (dsize--)
				{
					V front = qe.front();
					qe.pop();
					size_t index = GetVertexsIndex(front);
					visited[index] = true;
					for (size_t i = 0; i < _matrix.size(); i++)
					{
						if (_matrix[index][i] != W_MAX && visited[i] == false)
						{
							//找到了
							visited[i] = true;
							cout << _vertexs[i] << " ";
							qe.push(_vertexs[i]);
						}
					}
				}
				cout << endl;
				d++;
			}
		}

		// 图的DFS遍历，从某个顶点开始遍历
		void DFS(const V& Vertex)
		{
			size_t index = GetVertexsIndex(Vertex);
			vector<bool> visited(_vertexs.size(), false);
			_DFS(index, visited);
		}

		void _DFS(size_t index, vector<bool>& visited)
		{
			visited[index] = true;
			cout << _vertexs[index] << " ";
			for (size_t i = 0; i < _vertexs.size(); i++)
			{
				if (_matrix[index][i] != W_MAX && visited[i] == false)
				{
					_DFS(i, visited);
				}
			}
		}

图的存储结构和遍历的实现

#include <iostream>
#include <vector>
#include <map>
#include <queue>
#include <stack>
using namespace std;

namespace matrix
{
	// 顶点的类型，权值的类型，权值的最大值，是否是有向图
	template<class V, class W, W W_MAX = INT_MAX, bool Direction = false>
	class Graph
	{
	public:
		Graph(const V* vertexs, size_t n)
		{
			// 建立顶点和下标的映射关系
			for (size_t i = 0; i < n; i++)
			{
				_vertexs.push_back(vertexs[i]);
				_vIndexMap[vertexs[i]] = i;
			}

			_matrix.resize(n, vector<W>(n, W_MAX));
		}

		// 给一个顶点取出来它对应的下标
		size_t GetVertexsIndex(const V& vertex)
		{
			auto it = _vIndexMap.find(vertex);
			if (it != _vIndexMap.end())
			{
				return it->second;
			}
			else
			{
				throw invalid_argument("不存在的顶点");
				return -1;
			}
		}

		// 给邻接矩阵加值
		void _AddEdge(size_t srci, size_t dsti, W w)
		{
			_matrix[srci][dsti] = w;
			if (Direction == false)
				_matrix[dsti][srci] = w;
		}

		// 加边
		void AddEdge(const V& src, const V& dst, W w)
		{
			size_t srci = GetVertexsIndex(src);
			size_t dsti = GetVertexsIndex(dst);
			_AddEdge(srci, dsti, w);
		}

		// 显示邻接矩阵
		void Print()
		{
			// 打印顶点和下标映射关系
			for (size_t i = 0; i < _vertexs.size(); ++i)
			{
				cout << _vertexs[i] << "-" << i << " ";
			}
			cout << endl << endl;
			cout << "  ";
			for (size_t i = 0; i < _vertexs.size(); ++i)
			{
				cout << i << " ";
			}
			cout << endl;
			// 打印矩阵
			for (size_t i = 0; i < _matrix.size(); ++i)
			{
				cout << i << " ";
				for (size_t j = 0; j < _matrix[i].size(); ++j)
				{
					if (_matrix[i][j] != W_MAX)
						cout << _matrix[i][j] << " ";
					else
						cout << "#" << " ";
				}
				cout << endl;
			}
			cout << endl << endl;
			// 打印所有的边
			for (size_t i = 0; i < _matrix.size(); ++i)
			{
				for (size_t j = 0; j < _matrix[i].size(); ++j)
				{
					if (i < j && _matrix[i][j] != W_MAX)
					{
						cout << _vertexs[i] << "-" << _vertexs[j] << ":" <<
							_matrix[i][j] << endl;
					}
				}
			}
		}

		// 图的BFS遍历，从某个顶点开始遍历
		void BFS(const V& Vertex)
		{
			queue<V> qe;
			qe.push(Vertex);
			size_t d = 1;
			vector<bool> visited(_matrix.size(), false);
			while (!qe.empty())
			{
				size_t dsize = qe.size();
				cout << Vertex << "的" << d << "度好友:";
				while (dsize--)
				{
					V front = qe.front();
					qe.pop();
					size_t index = GetVertexsIndex(front);
					visited[index] = true;
					for (size_t i = 0; i < _matrix.size(); i++)
					{
						if (_matrix[index][i] != W_MAX && visited[i] == false)
						{
							//找到了
							visited[i] = true;
							cout << _vertexs[i] << " ";
							qe.push(_vertexs[i]);
						}
					}
				}
				cout << endl;
				d++;
			}
		}

		// 图的DFS遍历，从某个顶点开始遍历
		void DFS(const V& Vertex)
		{
			size_t index = GetVertexsIndex(Vertex);
			vector<bool> visited(_vertexs.size(), false);
			_DFS(index, visited);
		}

		void _DFS(size_t index, vector<bool>& visited)
		{
			visited[index] = true;
			cout << _vertexs[index] << " ";
			for (size_t i = 0; i < _vertexs.size(); i++)
			{
				if (_matrix[index][i] != W_MAX && visited[i] == false)
				{
					_DFS(i, visited);
				}
			}
		}

	private:
		// 下标到顶点的映射
		vector<V> _vertexs;
		// 邻接矩阵的存储
		vector<vector<W>> _matrix;
		// 顶点到下标的映射
		map<V, size_t> _vIndexMap;
	};
}

namespace list_table
{
	// 对于边的结构来说，需要存储的有边的两个顶点，边的权值，以及链接属性
	template <class W>
	struct Edge
	{
		Edge() = default;
		Edge(size_t srci, size_t dsti, W w)
			:_srci(srci)
			, _dsti(dsti)
			, _w(w)
			, _next(nullptr)
		{}
		size_t _srci;
		size_t _dsti;
		W _w;
		Edge<W>* _next;
	};

	// 顶点的类型，权值的类型，权值的最大值，是否是有向图
	template<class V, class W, bool Direction = false>
	class Graph
	{
		typedef Edge<W> Edge;
	public:
		Graph() = default;
		Graph(const V* vertexs, size_t n)
		{
			// 建立顶点和下标的映射关系
			for (size_t i = 0; i < n; i++)
			{
				_vertexs.push_back(vertexs[i]);
				_vIndexMap[vertexs[i]] = i;
			}

			_link_tables.resize(n, nullptr);
		}

		// 给一个顶点取出来它对应的下标
		size_t GetVertexsIndex(const V& vertex)
		{
			auto it = _vIndexMap.find(vertex);
			if (it != _vIndexMap.end())
			{
				return it->second;
			}
			else
			{
				throw invalid_argument("不存在的顶点");
				return -1;
			}
		}

		// 给邻接表加值
		void _AddEdge(size_t srci, size_t dsti, W w)
		{
			// 创建一个边的结构
			Edge* EdgePtr = new Edge(srci, dsti, w);
			Edge* tail = _link_tables[srci];
			while (tail && tail->_next)
				tail = tail->_next;
			// 把这个边的结构头插链入到邻接表
			if (tail == nullptr)
			{
				_link_tables[srci] = EdgePtr;
			}
			else
			{
				tail->_next = EdgePtr;
				tail = tail->_next;
			}
		}

		// 加边
		void AddEdge(const V& src, const V& dst, W w)
		{
			size_t srci = GetVertexsIndex(src);
			size_t dsti = GetVertexsIndex(dst);
			_AddEdge(srci, dsti, w);
			// 如果是无向图，就把对应的边也加到邻接表中
			if (Direction == false)
			{
				_AddEdge(dsti, srci, w);
			}
		}

		// 显示邻接矩阵
		void Print()
		{
			// 打印顶点和下标映射关系
			for (size_t i = 0; i < _vertexs.size(); ++i)
			{
				cout << _vertexs[i] << "-" << i << " ";
			}
			cout << endl;
			cout << endl;
			// 打印邻接表
			for (size_t i = 0; i < _link_tables.size(); ++i)
			{
				cout << i << " ";
				Edge* cur = _link_tables[i];
				while (cur)
				{
					cout << "[" << cur->_srci << "->" << cur->_dsti << "]" << "w->" << cur->_w << " ";
					cur = cur->_next;
				}
				cout << endl;
				cout << endl;
			}
			cout << endl << endl;
		}
	private:
		// 下标到顶点的映射
		vector<V> _vertexs;
		// 邻接表的存储
		vector<Edge*> _link_tables;
		// 顶点到下标的映射
		map<V, size_t> _vIndexMap;
	};
}