【正点原子】STM32电机应用控制学习笔记——8.FOC简介
FOC是适用于无刷电机的,而像有刷电机,舵机,步进电机是不适用FOC的。FOC是电机应用控制难度最大的部分了。
一.FOC简介(了解)
1.介绍
FOC(Filed Oriented Control)即磁场定向控制,又称磁场矢量控制(VC,Vector Control),也就是控制磁场的方向以及大小。
无刷电机的无感控制是六步换向,设定初始电流方向为u进入v流出,此时合成的磁场矢量方向是斜向下的,也就是吸引转子转动到这个位置,所以控制磁场也就是控制电机的转子。

FOC也是控制磁场,但是两者是有区别的。FOC有一个很明显的特点是精确,它可以非常精确的控制磁场的大小和方向,它可以使电机运转的转矩非常的平稳,噪声小,效率高,而且具有非常好的告诉动态响应。

六步换向是两两导通的一种方式,所以同一个时刻只有两项是导通的,绿色为电流流动方向,红色为合成的矢量方向,它是一段一段的位移的,走一圈全部运动了六段,一段走的是60度的角度。所以这个角度还是非常大的,在一些高精度的场合中,六步换向很显然是不行的,一点都不精确,像机械臂这些要求精度较高的,像素级别的精度,是不适用的。
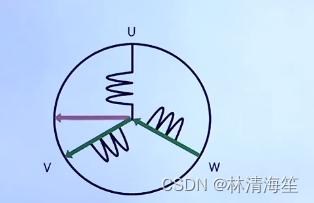
而FOC是三相同时导通的,每一项都是由导通的,只不过它分配的电流是有区别的,它就可以控制磁场的大小不变,实现360度无死角的旋转,这也是FOC和六步换向最大的区别了。
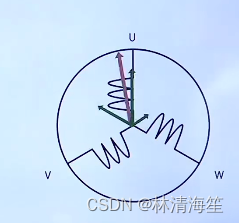
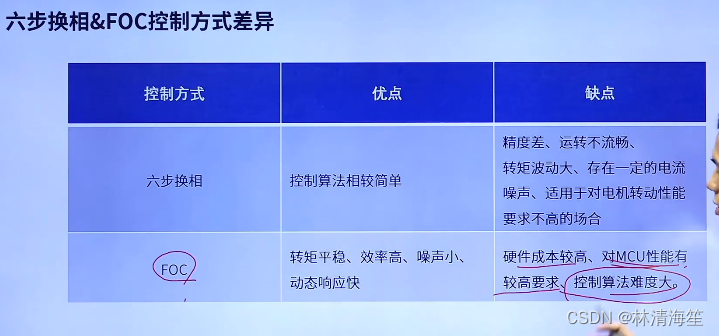
2.六步换向&FOC控制方式异同
首先六步换相的算法相对更加简单,但是缺点也非常明显,就是精度差,运转不流畅。所以无刷电机是没有位置环的,每一个位移都是60度或30度这么一个大角度,所以做位置环意义不大。且运转不流畅,因为是一段一段的移动,转矩的波动比较大,存在一定的电流噪声,适用于对电机转动性能要求不要的场合。
FOC优点非常明显,转矩平稳,效率高,噪声小,动态响应快,精度也非常大。但缺点就是硬件成本高,像FOC通常是使用PMSM无刷电机的,永磁同步电机的价格比较高,而且对MCU性能成本要求会更高。因为FOC涉及到数学物理学这方面的知识,算法难度会更大,所以控制算法的难度很大。
BLDC也是可以同样使用FOC的方式进行控制的,但是内部结构更适用六步换向。像FOC通常是用正弦波控制的,像BLDC通常用梯形波来控制的。PMSM电机在旋转的时候,去测量它的反电动势,是正弦波变化的。

二.FOC框图介绍(熟悉)
1.框图总体介绍
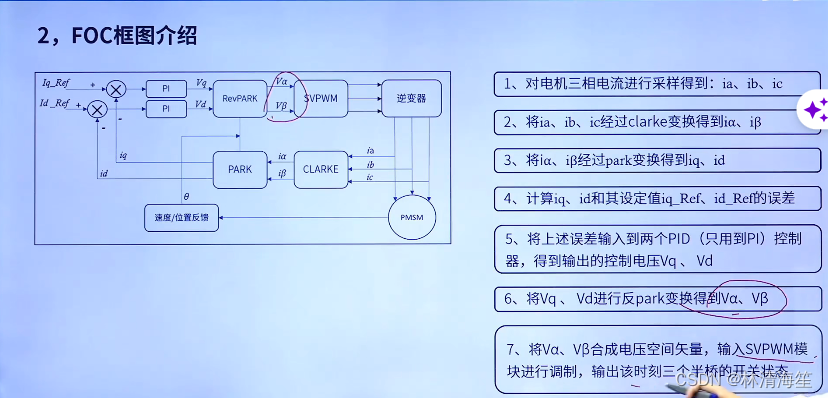
FOC整体的框图如下,在这里只用到PI运算。还是用了逆变器,也就是三相逆变电路,也就是通过三个半桥来控制电机。
总体过程:首先第一步是对电机的三相电流进行采样,就可以得到ia,ib,ic。采样之后经过CLARKE变换,就会得到iα和iβ。然后经过PARK变换,就会编程iq和id了。但同时还需要位置反馈,就是霍尔传感器,位置编码器这些来反馈转子的旋转角度。接着iq和id来到pi控制器了,这些设定值的误差来到PID控制器(只用到PI)算出期望值控制电压值Vq和Vd。接着进行反PARK运算,就能得到Vα和Vβ。接着就把它们输入到SVPWM模块中进行调制,输出控制三个半桥的开关状态,也就是六个开关。这样我们就可以控制PMSM或者BLDC了。
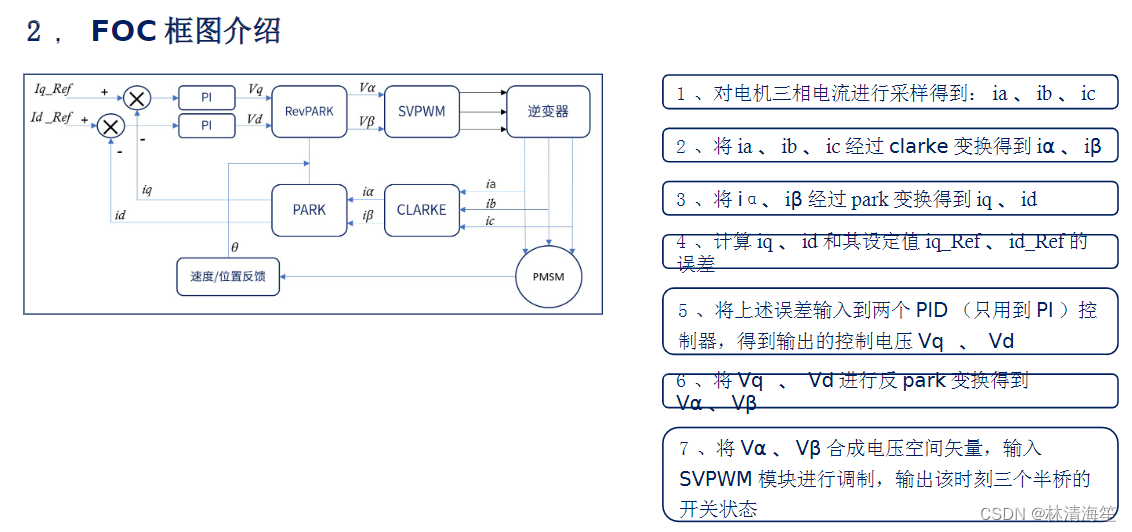
2.框图细分介绍
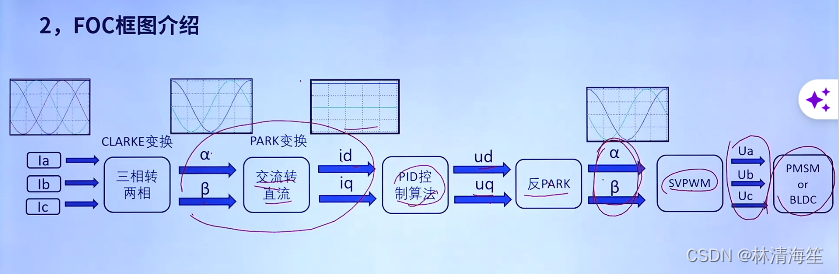
首先采集三相电流,经过CLARK变换。CLARK变换的作用可以简答理解为由三相转变为两项的作用。三相电流就是正弦波,120度的相位差的正弦波,转换之后就变成了α和β两项正弦波了。但是计算难度还是很大,因为是非线性不断变化的,方向大小都是不断变换的,去控制这样的变量难度是非常大的。
那么就需要经过PARK交流变换,交流转直流,转成直流之后就会变成线性的ip和iq。他们两个的值和方向都不改变了,进行正弦变量线性化了,这样控制会更加简单了。这样就能代入PID控制算法了,然后就可以输出Ud和Up电压了。之后来到反PARK变换,也就是跟前面PARK反过来的,将d和q变成α和β,也就是两项正弦波,因为svpwm需要用到这两个静止的坐标系,svpwm是需要使用到α和β,所以需要反变换过来,之后就输出ua和ub和uc来控制逆变电路,进而控制电机旋转起来。
在这里,我们可以把FOC的整个框图分为五个部分,第一部分是CLARKE变换,接着是PARK变换,接着是PID控制算法变换,反PARK,以及SVPWM。总共可以分为五个部分了。在后面会逐一拆开进行讲解。
3.常见问题
(1)为什么FOC要不断进行变换?
(2)什么是CLARKE变换,PARK变换和反PARK变换?
(3)α和β,d和q分别代表什么?
(4)什么是svpwm?
三.FOC控制核心——坐标变换(熟悉)
1.旋转的PMSM电机波形
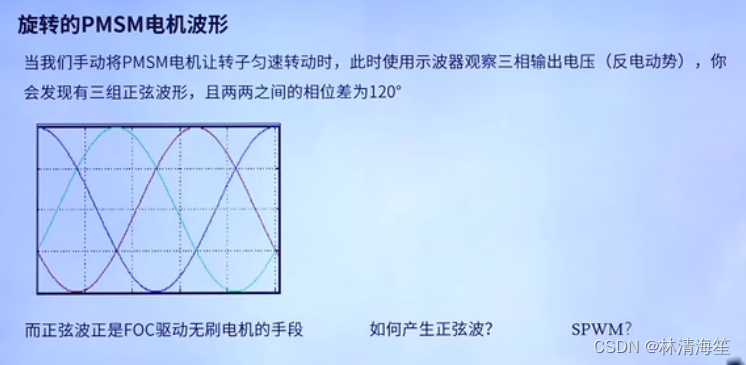
这里可以使用手动去让电机的转子匀速转动,然后就能使用示波器来观察三相饶阻uvw输出的电压,以及检测反电动势。所以速度不能太小,如果太小的话反电动势是非常小的,这时候会检测不出来了。所以这里要保持一定的速度。接着就会发现示波器出现三组正弦波了。它们之间还有相位差120度。
那么我们要控制电机旋转起来,就是输出这三项的正弦波才能使电机旋转起来。而这个正弦波正是FOC驱动无刷电机的手段。
那么这里有一个问题,如何才能产生正弦波呢?如果使用PWM模拟正弦波,那么就是SPWM了
2.SPWM
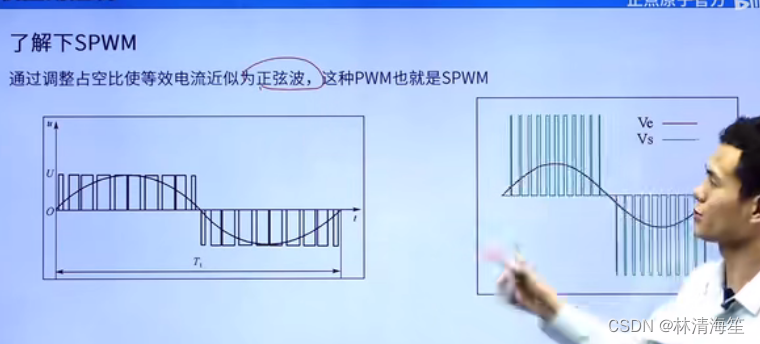
SPWM就是通过调整占空比的大小使其等效电流近似与正弦波。
比如,有一个LED灯,通过PWM控制。假设100%占空比输出10v,如果为50%,电压就会变为5v,如果为10%,就位1v。电压大小是可以通过电压大小来进行改变。正弦波的电压就是不断在改变的,可以使用不同的占空比来实现电压的变换。这样在经过低通滤波器之后就能得到一个正弦波了。
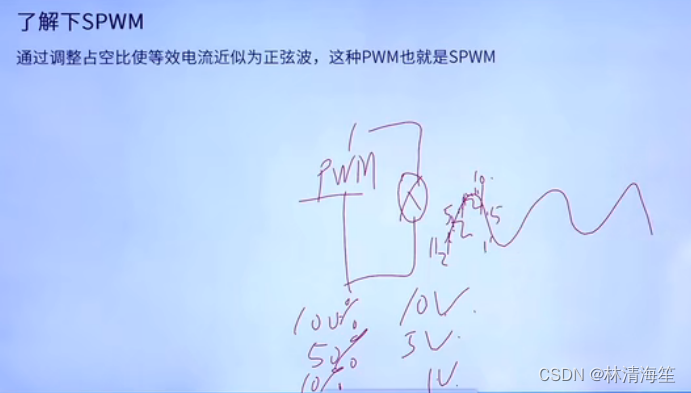
如下图,不同的占空比大小对应的电压是不一样的。这样就可以模拟出正弦波了。
右图绿色就是占空比大小,红色就是不同的占空比对应的电压值了。很明显占空比越大所对应的电压值也越大。那么我们就可以按照这种规律,一段一段的组合到一起,就可以形成正弦波了。
但是要注意SPWM是不依赖开关顺序的,3相之间时独立调制的。也就是说ABC各自有半桥电路,就能组成各自的三相逆变电路了,然后他们各自之间输入正弦波,就只负责生成正弦波,不管电机的任何状态,也不管电机的任何参数,就只负责输入正弦波,是没有任何反馈的,类似开环控制。但是这种系统是非常不稳定的。
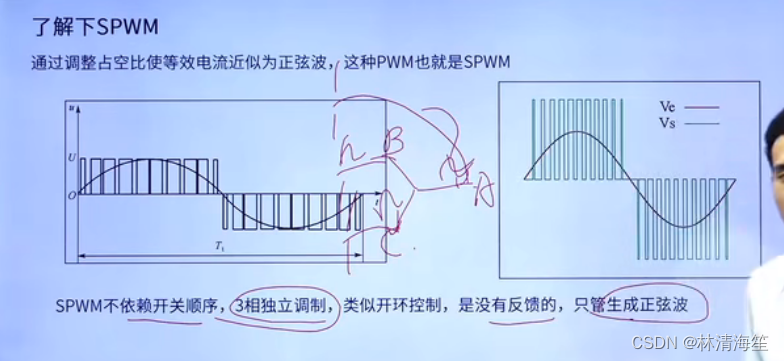
所以说SPWM调试方式在FOC上是不常用的,还有一个原因是SPWM的母线电压利用率要比SVPWM的母线电压利用率要低15%。
而且从控制的角度来看,不想跟三个正弦波来打交道的。因为要控制正弦波,难度是非常大的。因为正弦波是非线性的量。大小和方向都是不断改变的。

3.坐标变换
1)CLARKE变换
将三相转换成两相,因为三相电路计算是比较困难的。变换的原则是变换前后电流产生的磁场是必须相等的。
将三相电流的坐标系转换成直角坐标系α和β。
同时,三相电流是不需要同时检测的,通常来说只需要检测两项,另外一项可以通过KCL,得到
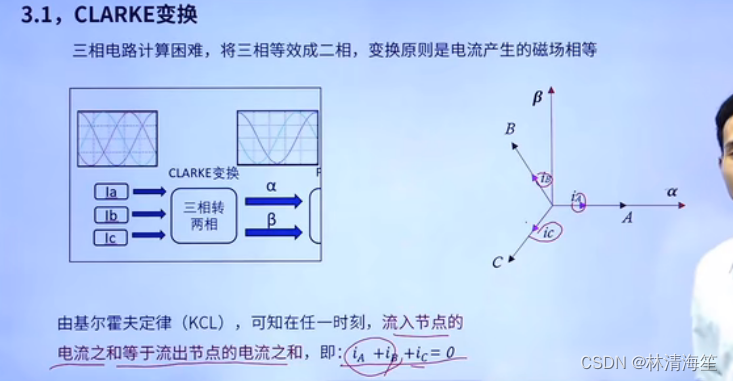
通过将abc三相电流进行正交分解。

虽然α和β坐标系少了一维变量,但新的变量还是正弦波,所以还要进行操作变成线性化。
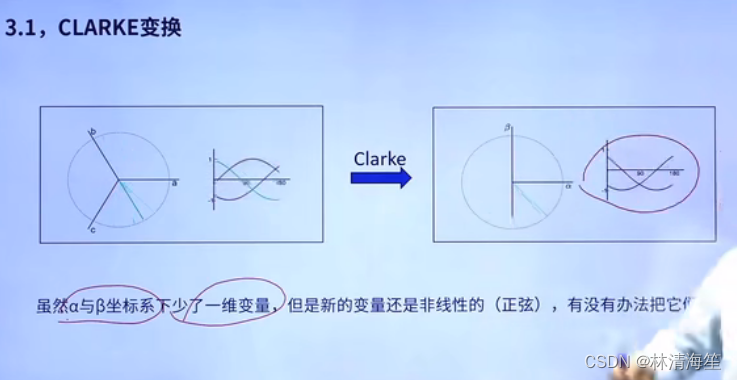
2)PARK变换
将α和β转化为id和iq。
PARK变换就是将两相静止坐标系转换为随转子转动的坐标系,也就是dq轴。
d轴的方向是与转子内磁场的方向重合,也就是直轴。q轴的方向与转子内磁场的方向垂直,为交轴。
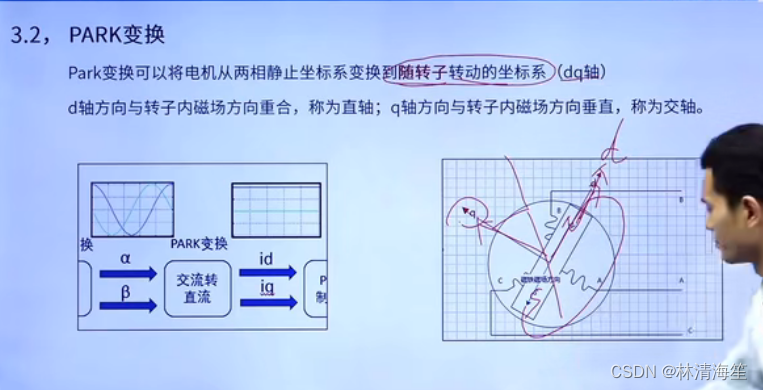
建设将α-β坐标系旋转θ角度(也就是转子旋转的角度,这个角度是可以通过霍尔或者位置编码器测出来的。)同样,也是将α-β轴进行正交分解。
这两个坐标系的两个控制量是线性的,就可以带入到PID控制器里面了。通过PID运算器运算出想要的期望值来进行控制。

3)反PARK变换
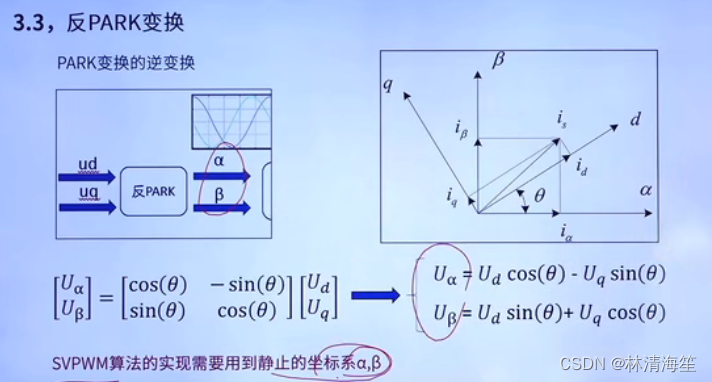
就是将dq分解为α和β坐标系。Ud和Uq是PID控制器得到的坐标值。
经过反PARK变换是因为SVPWM算法需要α和β两个静止坐标系的。算法需要通过这两个变量得到的。
四.FOC闭环回路(熟悉)
1.PID控制器
这部分也就是PID控制器。PID控制器通常有三个环,第一个是电流环,通常作为最内环,通过电流反馈来得到电机电流的扭矩。
接着就是速度环,控制电机的转速的。
然后是位置环,控制电机的旋转位置。
先讲解的是电流环。
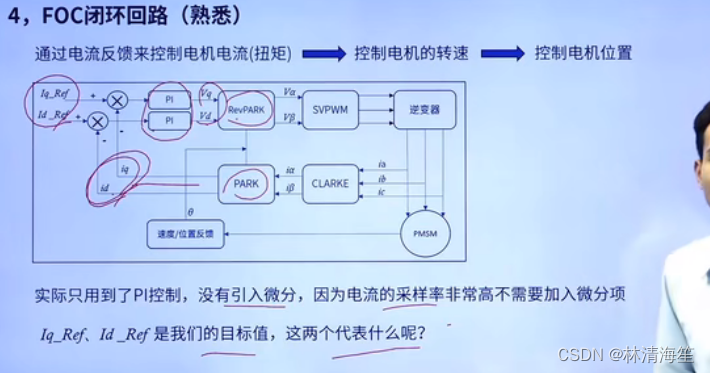
经过一系列变换后输出的是iq和id。然后跟目标值进行相减来得到的误差来进行PI运算。这里要注意的是这里只用到了PI控制,没有引入微分。因为电流的采样率是非常搞得,就不需要微分项了。输出的期望值之后再经过反PARK变换。
那么这里有一个疑问,iq和id的两个目标值分别代表的是什么?
2.电流环和FOC的意义
那么就需要了解FOC它的意义和目的。
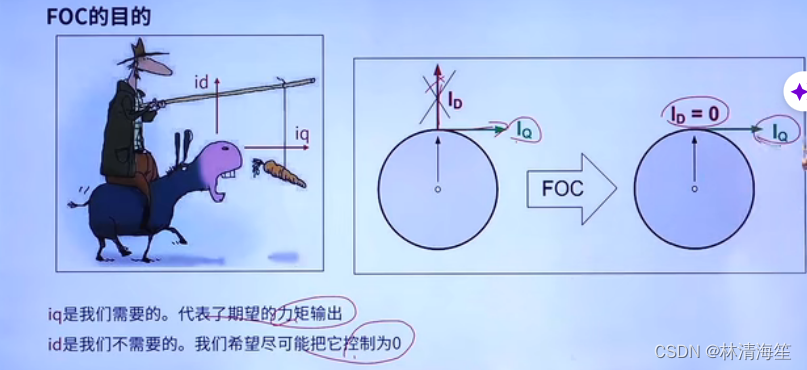
下面通过一个漫画进行演示,对于老头来说,是希望驴是一直往前走的,那么老头就会吊着一个萝卜,就给了驴向前走的驱动力,称为iq,当iq越大,驴走的就越快,越小走得就越慢。所以iq是我们需要的。id是我们不需要的,因为驴不用飞。
对比我们的电机,FOC也是一样的,对于转子来说,切线方向的iq是需要的,因为它驱动转子的一个力矩。与半径同方向的id是我们不需要的,只会增加我们的电流,让我们的电流让电机发热,
所以说id尽可能让电机控制到0,iq就是我们所期望的力矩输出。
所以电流环的两个目标值,iq就是我们期望的力矩输出,id的目标输出设置为0.
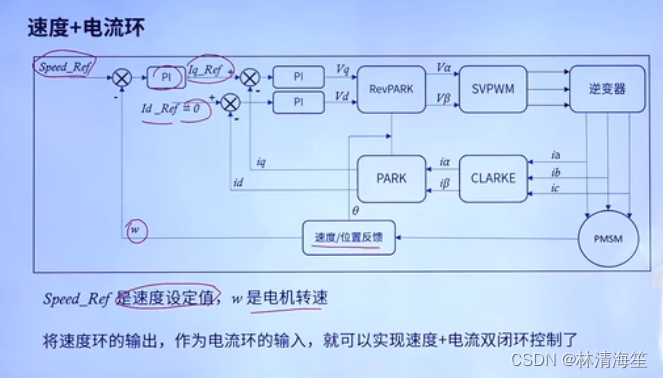
3.速度+电流环
这就是在之前的基础上加上速度环。
首先Speed_ref就是速度的目标值了,w就是实际的电机转速,可以通过编码器或者霍尔传感器检测出来的,算出来的误差经过PI运算之后,将他们的输出值当做电流环的输入,iq就是我们期望的力矩输出。然后id是将尽可能控制到0。这样我们就能实现速度+电流双闭环控制了。
4.位置+速度+电流环
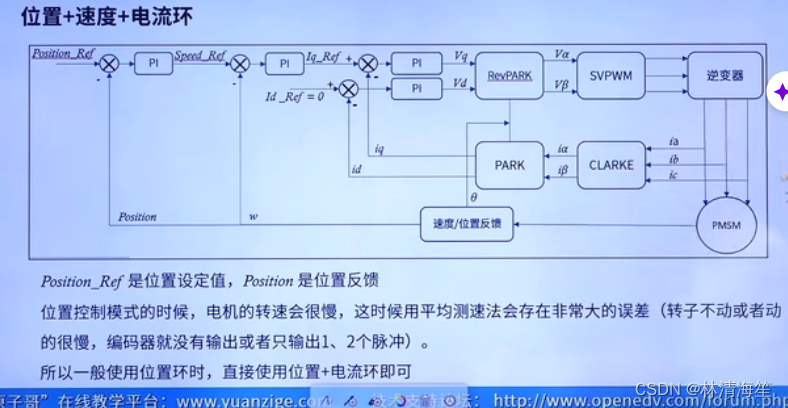
这在前面的基础上加上了位置环。
Position_ref是位置的期望值,position是实际的位置。然后将速度环的输出当做电流环的输入。这样就能实现三闭环了。
但是我们要注意了,位置环的电机转速会相对来说比较慢。那么如果我们使用平均测速方法误差就比较大了(因为转子要么不动要么动得很慢)此时编码器输出就只有几个波形了。所以对速度环的误差是比较大的,比较波动。所以在使用位置环的时候,就直接使用位置+电流双闭环即可。就可以把中间的速度环给去掉了。这样能够更加稳定一点。
五.SVPWM解析(熟悉)
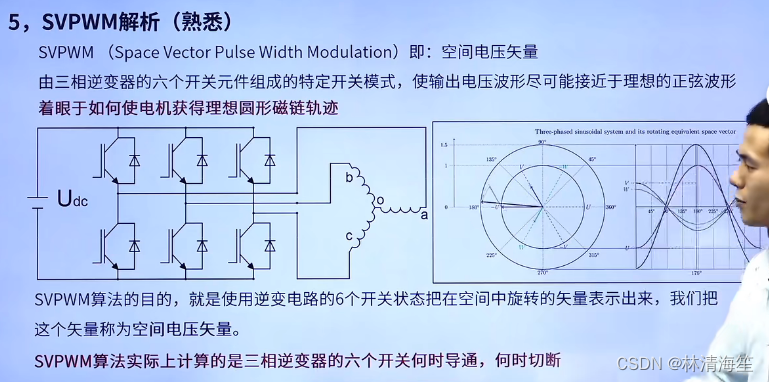
SVPWM(Space Vector Pluse Width Modulation)即空间电压矢量。它是由三相逆变器的六个开关元件组成的特定开关模式,使输出的电压波形尽可能接近于理想的正弦波形。也就是通过六个mos管组合使我们组合输出三项的相电压成正弦变化给无刷电机,让其旋转起来。因为FOC就是输出正弦波让无刷电机驱动起来的。这个步骤就是有SVPWM来实现的。
可以看到右边的动态示意图,这里有uvw三相,对应的就是abc这三相了。这三相有他们各自的电压矢量,它们的大小都是随时间成正弦规律变化的。这三个电压矢量它会合成一个总矢量,可以发现这个总矢量的大小的不变的,方向不断改变。这也是为什么FOC合成的力矩会更加的平稳。这也跟前面说的SPWM是不一样的,因为其三相是独立调制的,它只负责提供正弦波。那么SVPWM是把整个看成一个整体,着眼于如何使电机或得一个理想的圆形磁链轨迹。
所以SVPWM的目的,就是控制逆变电路的6个开关状态把在空间中旋转的矢量表示出来,这个矢量也就是空间电压矢量。
所以SVPWM算法实际上就是计算三相逆变器的六个开关何时导通,何时关闭。
三相逆变器一共有八种组合,
然后,我们定义了一个开关函数Sx。
当Sa=1的时候代表上桥臂导通,Sa=0则表示下桥臂导通(同一个半桥补课同时导通上下桥臂)
所以总共有八种组合。
六种非零矢量。U1(001)表示a下桥臂b下桥臂c上桥臂导通,既有上桥臂又有下桥臂就会产生电压差,有电压差就会有有向电流。这种有向电流的矢量称为非零矢量。
零矢量表示abc三个桥臂同时接下桥臂或者上桥臂。这样就不会产生电压差的,也就没有有向电流。

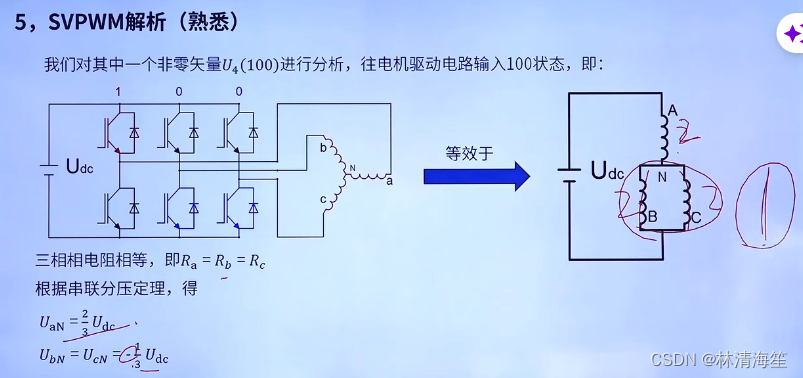
下面以U4(100)来分析,a上bc下桥臂导通,从a相电流流向b和c相。这就等效于右图的电路。
此时他们三相的相电阻是相等的。通过串联分压定理可以得到Uan为2/3Udc
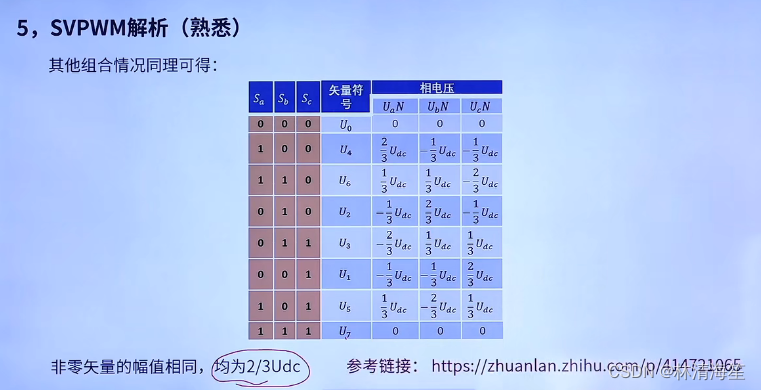
其他组合同理,这里给出了其他组合的表格。
可以发现非零矢量的幅值是相同的,均为2/3Udc。
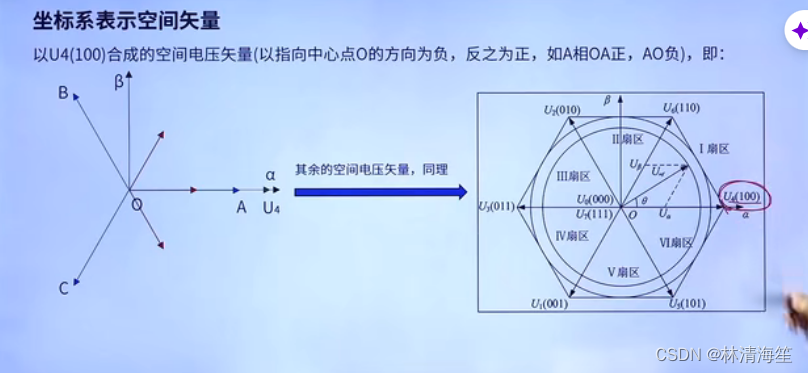
注意电压是标量,电压矢量是矢量,矢量的正方向是由我们自己定义的。这里定义以指向中心点o的方向为负,反之为正。
由于a接上桥臂,所以是正方向OA。bc接下桥臂,所以方向为负。他们所合成的电压矢量为U4。
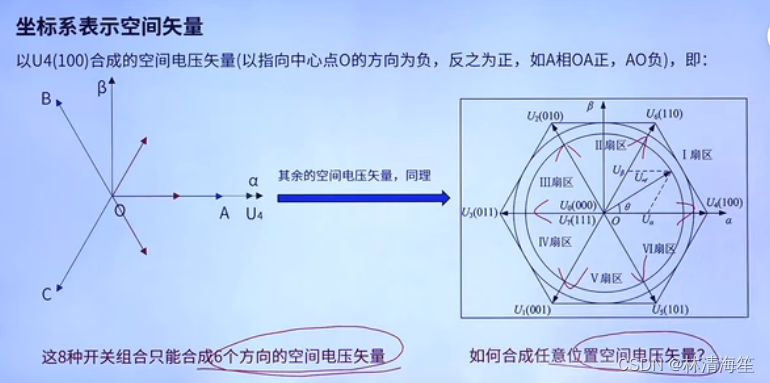
其他组合同理,就能得到右图的六边形图。零矢量是没有有向电流的,所以它就在原点处。
但这里会有一个疑问,这八种开关组合只能合成六个方向的空间电压矢量。那么我们应该如何合成任意位置的空间电压矢量呢?
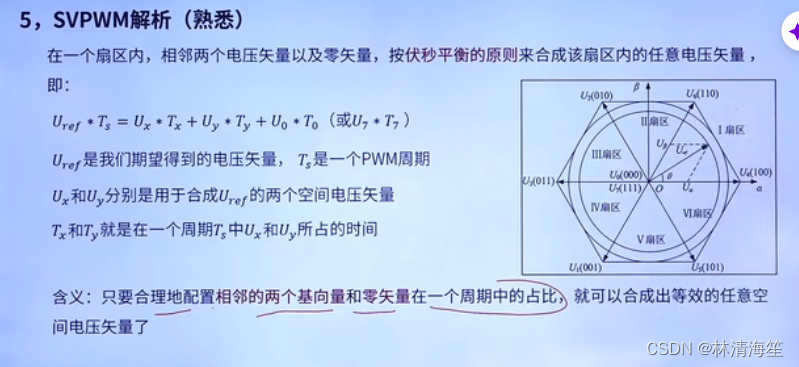
那么在这里以扇区为单位,在一个扇区内,相邻两个电压矢量以及零矢量,按照伏秒平衡的原则来合成该扇区内的任意位置的电压矢量。就是满足下面的关系式。
Uref就是期望得到的电压矢量,也就是任意位置的电压矢量,Ts是一个PWM周期,也就是定时器周期。
Ux和Uy分别是用于合成Uref的两个空间电压矢量。
Tx和Ty就是在一个周期中Ux和Uy所占的时间。
那么假设Uref在第一扇区,那么Ux和Uy就是其相邻两个矢量U4和U6,以及零矢量U0和U7了,来合成这个Uf。主要区别是他们各自时间的占比Tx和Ty。只要算出各自的时间占比,就能算出任意位置的空间电压矢量了。
所以问题1:如何计算相邻电压矢量与零矢量在一个周期内的时间占比?还有就是扇区的判断了,因为每一个扇区相邻的矢量是不一样的。

首先我们假设在扇区一,通过U4和U6两个矢量合成Uref,就满足伏秒平衡的公式。
Uref等于相邻的电压矢量乘以他们的时间,还有零矢量。
接着就对期望的电压矢量进行分解,分解到α和β轴。
U4和U6实际上就是2/3Udc。
由于U4整个都是α轴上,所以其在α轴上的分量为1,在β轴上的分量为0。
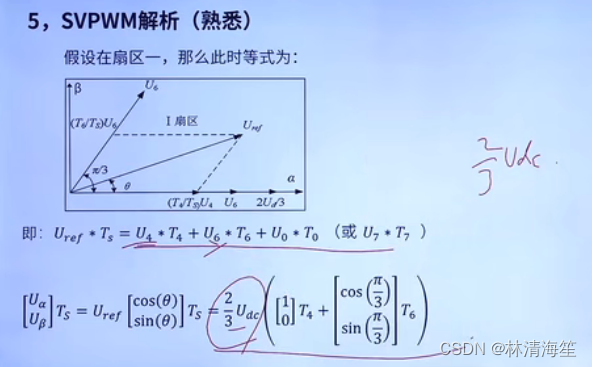
最终解得算到α和β,和前面的PARK变换联系上了。
Ts减去T4再减去T6就是剩下零矢量的时间了。这里零矢量的时间是可以自由分配的,在这里平均分配给T0和T7,所以剩余的零矢量除以2进行分配。
在这里是以七段式的SVPWM为例。
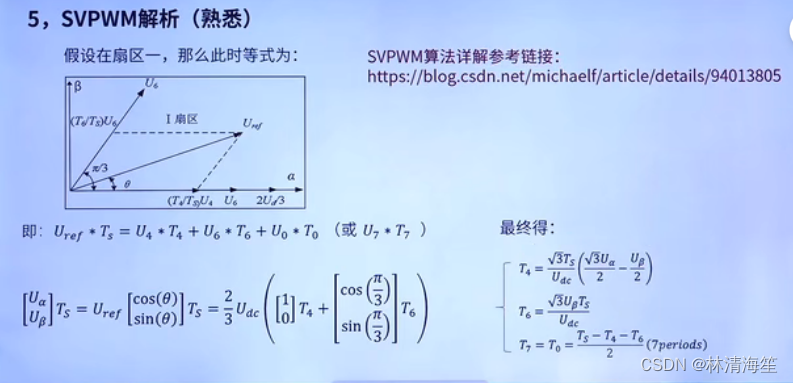
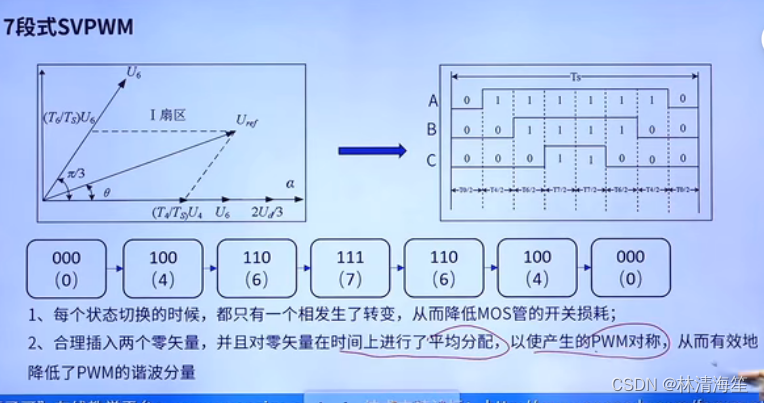
- 七段式SVPWM
同样还是以第一个扇区为例。
在前面我们已经算出了T4,T6,T0,T7对应每个电压矢量所持续的时间,我们只要保证电压矢量持续这么长的时间,就可以合成这一个期望矢量Uref。
但是七段式的SVPWM它有自己的一个顺序(如右图),第一步U0持续T0/2的时间,第二步U4持续T4/2的时间,然后是U6持续T6/2的时间,U7持续T7/2的时间,然后反过来,U7持续T7/2的时间,U6持续T6/2的时间…………整个时间加起来就是T7,T4,T6,T0。这跟之前的是等效的,但是在实际应用中要考虑到mos管的开关损耗。
所以我们可以发现,这七段式的SVPWM的每一个变化就只有一相发生了变化。所以这可以大大降低mos管的开关损耗。
除此之外,还合理插入了两个零矢量,并且对零矢量上对时间进行平均分配,可以使产生的PWM堆成,从而有效的降低了PWM的谐波分量。
这样我们就可以求出了相邻的两个电压矢量的时间,以及零矢量的时间。就可以看出这个波形了,其他的扇区也是同理的。
然后我们就可以去设置它的占空比,去比较值,就可以使PWM输出这样的波形了。就可以使三相去合成想要的矢量了。
- 扇区的判定
那么这里还剩下一个疑问,如何判断期望的电压矢量所在的扇区呢?因为不同的扇区所用的基向量是不一样的。
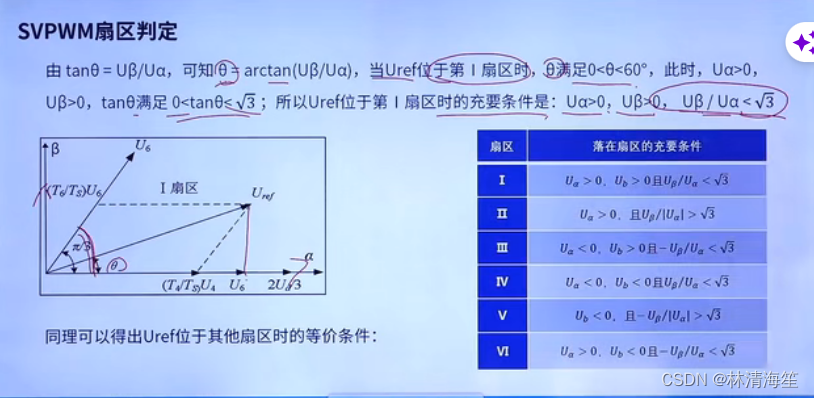
同样在这里以扇区1为例,θ值可以通过Uβ比上Uα的反正切值来得到。当期望电压Uref在第一个扇区的时候,此时θ满足0~60度之间,而且α和β都是大于0的。所以tanθ在0到根号3之间。然后我们就可以没到Uref在第一扇区的充要条件是
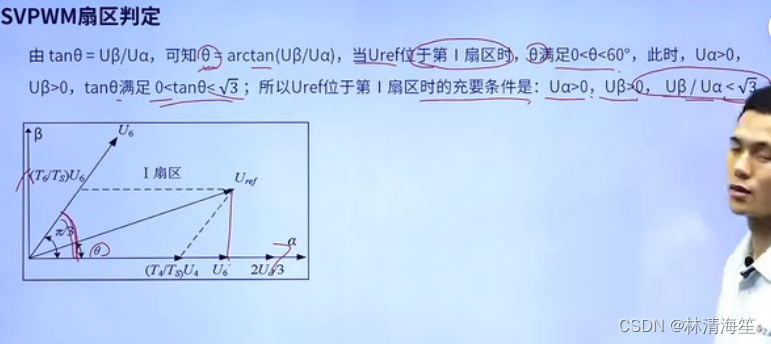
那么在其他扇区同理,已经在下图的表格中展示出来了。那么这样就解决了SVPWM的扇区判定了。那么判断完扇区之后,就可以求出相邻的两个矢量以及零矢量所持续的时间了。
六.课堂总结(掌握)


本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Vue3Ts中如何实现父组件传递给子组件
- 为什么应届毕业生开始学Python语言?(附Python零基础入门教程)
- 一个黑客的真实收入到底是多少?鼠标一点,轻轻松松到账一个小目标?
- 处理数组,将一维转二维
- 精品量化公式——“低位擒妖”,擒妖指标终极版,成功率百分99,无未来
- MicroPython ESP32开发板上的锂电池连接器型号是什么?
- 【C语言】扫雷小游戏(保姆教程)
- JAVA基于遗传算法的中药药对挖掘系统的设计与实现(源代码+论文)
- 自然语言转SQL,一个微调ChatGPT3.5的实例(上)--训练数据准备
- 环境变量详细说明