每日算法打卡：递归实现指数型枚举 day 1

原题链接

92. 递归实现指数型枚举

题目难度：简单

题目描述

从 $1～n$ 这 n 个整数中随机选取任意多个，输出所有可能的选择方案。

输入格式

输入一个整数 n。

输出格式

每行输出一种方案。

同一行内的数必须升序排列，相邻两个数用恰好 1 个空格隔开。

对于没有选任何数的方案，输出空行。

本题有自定义校验器（SPJ），各行（不同方案）之间的顺序任意。

数据范围

$1\le n\le 15$

输入样例：

3 

输出样例：

3
2
2 3
1
1 3
1 2
1 2 3 

题目分析

这道题目的意思其实一目了然，然后我们可以根据数据范围选择出算法复杂度，实际上是$O(2^n)$级别即可

我们主要的思路就是需要确定从$1～n$中确定出这个数是选还是不选，因此所有的情况数就是$2^n$了

这道题的目的其实是训练我们递归的思想，对于递归(dfs)最重要的就是顺序，需要不重不漏的把所有可能的方案都顾及到，具体到这道题我们就只需要从$1～n$依次考虑选和不选的两种情况

这样我们就可以画一个递归树

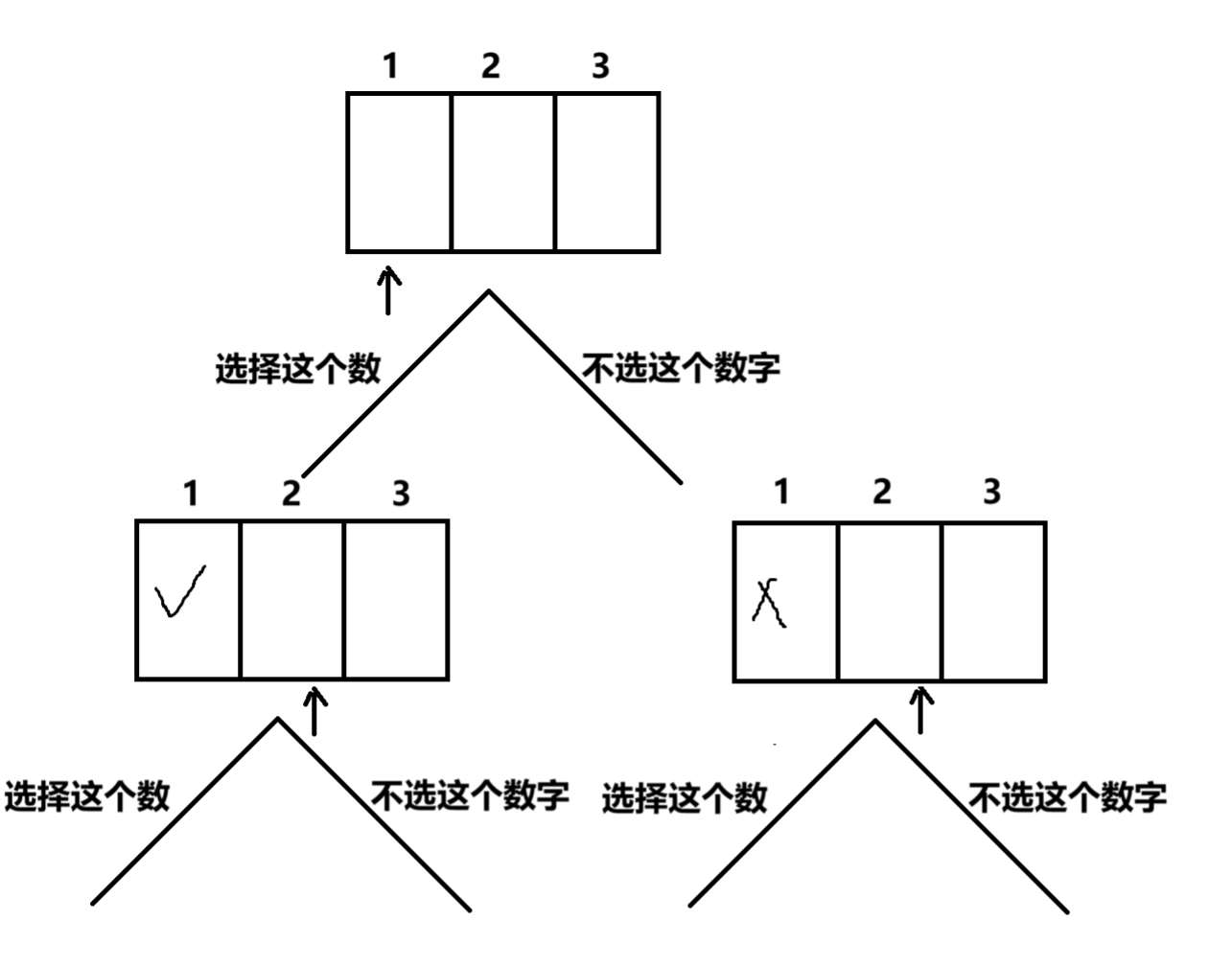
这里我们也称之为递归搜索树，我们以三个数字为例，实际上是可以通过这种方法枚举出所有情况的，接下来的问题就是我们如何去实现，如何记录每一种情况下的状态

这里的状态我们有两种方法，一是开一个长度为$n$的数组，第二种方法就是利用位运算，将数位为1的位置标记为选中，将数位为0的位置标记为未选中

这里我们采用第一种方法来实现，因为比较直观容易理解

#include<iostream>
using namespace std;

const int N = 15;

int n;
int state[N]; // 状态数组，用于记录每个位置上的数据是否被选中，我们使用1表示选中，-1表示未选中，0表示还轮到他选

void dfs(int cur) // cur 表示当前在第cur位
{
    // 递归首先要确定边界情况
    if (cur == n)
        // 当我们每一次搜索到最后一个数字的时候需要从前往后遍历每一位，判断这个位置上的数据是否被选中，如果被选中，就需要输出
    {
        for (int i = 0; i < n; i++)
        {
            if (state[i] == 1)
            {
                cout << (i + 1) << ' '; // 这里因为刚好是从1到n的数，我们可以借用i来表示
            }
        }
        cout << '\n';
        return;
    }
    state[cur] = 1; // 表示选择这个位置的数据
    dfs(cur + 1); // 递归到下一个位置
    state[cur] = 0; // 恢复成没有开始选择这个位置的情况

    state[cur] = -1;
    dfs(cur + 1);
    state[cur] = 0;
}

int main()
{
    cin >> n; // 输入数据
    dfs(0); // 表示从第0位开始递归
    return 0;
}

对于递归的情况，我们在回到上一步的时候，需要恢复原来的样子，不然再次进行操作时，可能会引出错误的情况，需要保持这个习惯，其次我们在写递归函数的时候，需要首先考虑何时递归结束

感谢各位的支持，如果你发现文章中有任何不严谨或者需要补充的部分，欢迎在评论区指出