哈希桶的模拟实现【C++】
哈希冲突解决
闭散列 (开放定址法)
发生哈希冲突时,如果哈希表未被装满,说明在哈希表种必然还有空位置,那么可以把产生冲突的元素存放到冲突位置的“下一个”空位置中去
如何寻找“下一个位置”
1、线性探测
发生哈希冲突时,从发生冲突的位置开始,依次向后探测,直到找到下一个空位置为止
Hi=(H0+i)%m?( i = 1 , 2 , 3 , . . . )
H0:通过哈希函数对元素的关键码进行计算得到的位置。
Hi:冲突元素通过线性探测后得到的存放位置
m:表的大小。
举例:
用除留余数法将序列{1,111,4,7,15,25,44,9}插入到表长为10的哈希表中,当发生哈希冲突时我们采用闭散列的线性探测找到下一个空位置进行插入,插入过程如下:
使用除留余数法
1%10 =1 ,111 %10 =1
即111和1发生了哈希冲突 ,所以111找到1的下一个空位置插入

将数据插入到有限的空间,那么空间中的元素越多,插入元素时产生冲突的概率也就越大,冲突多次后插入哈希表的元素,在查找时的效率必然也会降低。
介于此,哈希表当中引入了负载因子(载荷因子):
负载因子 = 表中有效数据个数 / 空间的大小
不难发现:
负载因子越大,产出冲突的概率越高,查找的效率越低
负载因子越小,产出冲突的概率越低,查找的效率越高
负载因子越小,也就意味着空间的利用率越低,此时大量的空间都被浪费了。对于闭散列(开放定址法)来说,负载因子是特别重要的因素,一般控制在0.7~0.8以下
采用开放定址法的hash库,如JAVA的系统库限制了负载因子为0.75,当超过该值时,会对哈希表进行增容
线性探测的缺点:一旦发生冲突,所有的冲突连在一起,容易产生数据“堆积”,即不同关键码占据了可利用的空位置,使得寻找某关键码的位置需要多次比较(踩踏效应),导致搜索效率降低
2、二次探测
二次探测为了避免该问题,找下一个空位置的方法为
Hi=(H0+i ^2 )%m?( i = 1 , 2 , 3 , . . . )
H0:通过哈希函数对元素的关键码进行计算得到的位置
Hi:冲突元素通过二次探测后得到的存放位置
m:表的大小
相比线性探测而言,二次探测i是平方,采用二次探测的哈希表中元素的分布会相对稀疏一些,不容易导致数据堆积
template <class K>
struct DefaultHashFunc
{
size_t operator() (const K& key)
{
return (size_t)key;
}
};
template <>
struct DefaultHashFunc<string>
{
size_t operator() (const string& str)
{
//BKDR,将输入的字符串转换为哈希值
size_t hash = 0;
for (auto ch : str)
{
hash *= 131;
hash += ch;
}
return hash;
}
};
namespace open_address
{
enum STATE
{
EXIST,
EMPTY,
DELETE
};
template<class K, class V>
struct HashData
{
pair<K, V> _kv;
STATE _state = EMPTY;
};
struct StringHashFunc
{
size_t operator()(const string& str)
{
return str[0];
}
};
//template<class K, class V>
template<class K, class V, class HashFunc = DefaultHashFunc<K>>
class HashTable
{
public:
HashTable()
{
_table.resize(10);
}
bool insert(const pair<K, V> kv)
{
//扩容
if ((double)_n / (double)_table.size() >= 0.7)
{
HashTable<K, V> newHT;
size_t newSize = _table.size() * 2;
newHT._table.resize(newSize);
//遍历旧表的数据,将旧表的数据重新映射到新表中
for (size_t i = 0; i < _table.size(); i++)
{
if (_table[i]._state == EXIST)
{
newHT.insert(_table[i]._kv);//插入的写成kv不行?
}
}
_table.swap(newHT._table);
}
//线性探测
HashFunc hf;
size_t hashi = hf(kv.first) % _table.size();
//如果该位置没有元素,则直接插入元素 ,如果该位置有元素,找到下一个空位置,插入新元素
while (_table[hashi]._state == EXIST)//不是EMPTY和DELETE这两种情况
{
++hashi;
hashi %= _table.size();
}
//是EMPTY和DELETE这两种情况
_table[hashi]._kv = kv;
_table[hashi]._state = EXIST;
++_n;
return true;
}
HashData<const K, V>* Find(const K& key)
{
HashFunc hf;
//线性探测
//如果该位置没有元素,则直接插入元素 ,如果该位置有元素,找到下一个空位置,插入新元素
size_t hashi = hf(key) % _table.size();
while (_table[hashi]._state != EMPTY) //DELETE和EXIST
{
if (_table[hashi]._state == EXIST && _table[hashi]._kv.first == key)
{
return (HashData<const K, V>*) & _table[hashi];
}
}
return nullptr;
}
bool Erase(const K& key)
{
//先找到
HashData<const K, V>* ret = Find(key);
//再删除
if (ret != nullptr)
{
ret->_state = DELETE;
_n--;
return true;
}
//没找到
return false;
}
public:
vector<HashData<K, V>> _table;
size_t _n = 0; //存储有效数据的个数
};
}
闭散列最大的缺陷就是空间利用率比较低,这也是哈希的缺陷
开散列 (链地址法、哈希桶)
开散列,又叫哈希桶,首先对关键码集合用哈希函数计算哈希地址,具有相同地址的关键码归于同一子集合,每一个子集合称为一个桶,各个桶中的元素通过一个单链表链接起来,各链表的头结点存储在哈希表中
举例:
用除留余数法将序列{1,111,4,7,15,25,44,9}插入到表长为10的哈希表中,当发生哈希冲突时我们采用开散列的方式进行插入,插入过程如下:

将相同哈希地址的元素通过单链表链接起来,然后将链表的头结点存储在哈希表中的方式,不会影响与自己哈希地址不同的元素的增删查改的效率,因此开散列的负载因子相比闭散列而言,可以稍微大一点
闭散列的开放定址法,负载因子不能超过1,一般建议控制在[0.0, 0.7]
开散列的哈希桶,负载因子可以超过1,一般建议控制在[0.0, 1.0]
在实际中,开散列的哈希桶结构比闭散列更实用,主要原因有两点:
哈希桶的负载因子可以更大,空间利用率高
哈希桶在极端情况下还有可用的解决方案
开散列实现(哈希桶)
哈希表的结构
struct HashNode
{
pair<K, V> _kv;
HashNode<K,V>* _next;
HashNode( const pair<K, V> & kv)
:_kv(kv)
,_next(nullptr)
{
}
};
Insert
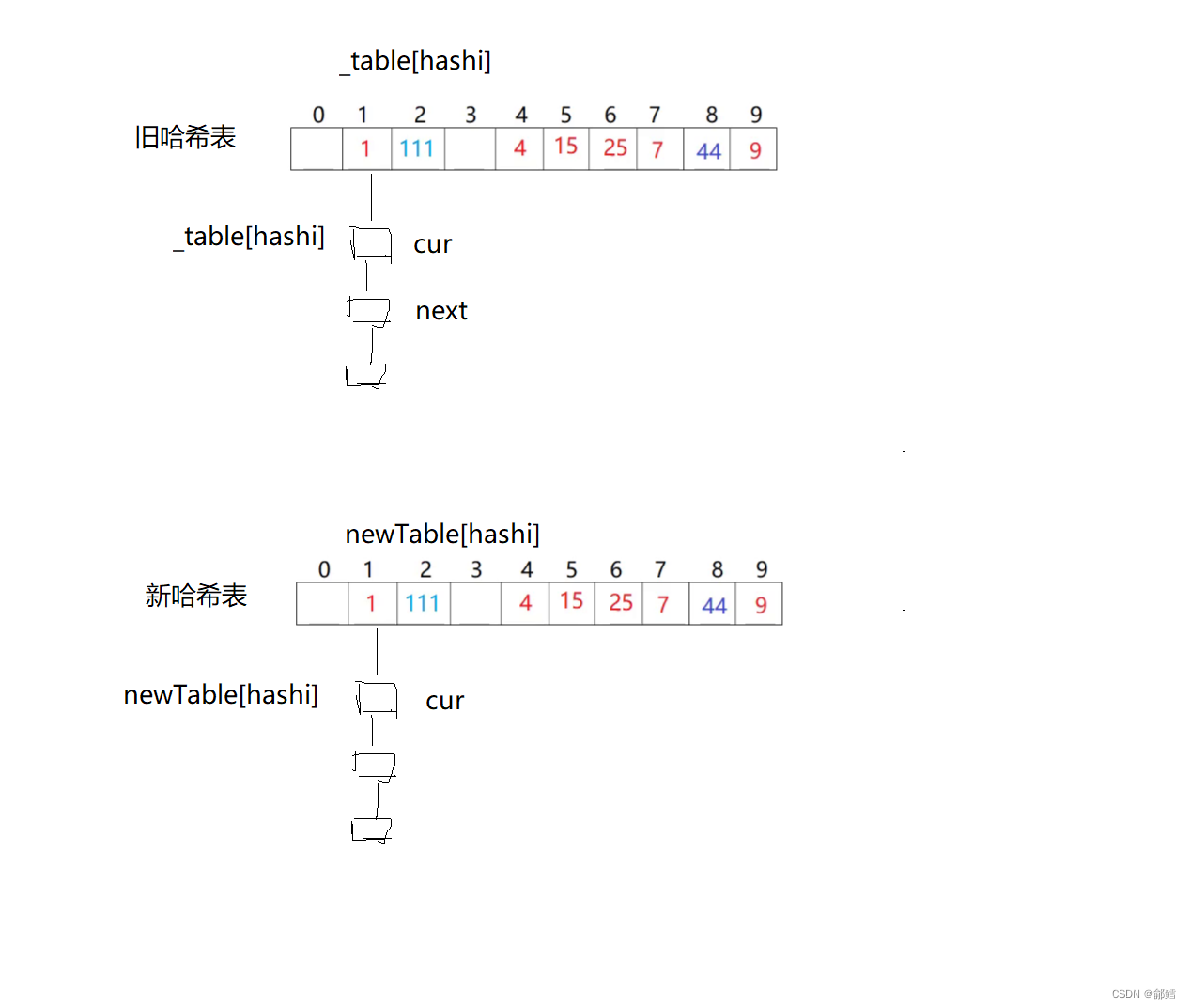
bool Insert(const pair<K,V> & kv)
{
size_t hashi = kv.first % _table.size();
//负载因子到1就扩容
if (_n == _table.size())
{
size_t newsize = _table.size() * 2;
vector<Node*> newTable;
newTable.resize(newsize, nullptr);
//遍历旧表,将原哈希表当中的结点插入到新哈希表
for (int i = 0; i <= _table.size(); i++)
{
Node* cur = _table[i];
//插入到新哈希表
while (cur != nullptr)
{
Node* next = cur->_next;
// 重新分配hashi
size_t hashi = cur->_kv.first % _table.size();
cur->_next = newTable[hashi];
newTable[hashi] = cur;
cur = next;
}
}
}
//头插
Node* newnode = new Node(kv);
newnode->_next = _table[hashi];
_table[hashi] = newnode;
return true;
}
Find
Node * Find(const K & key)
{
size_t hashi = key % _table.size();
Node* cur = _table[hashi];
while (cur != nullptr)
{
if (key == cur->_kv.first)
{
return cur;
}
cur = cur->_next;
}
return nullptr;
}
Erase
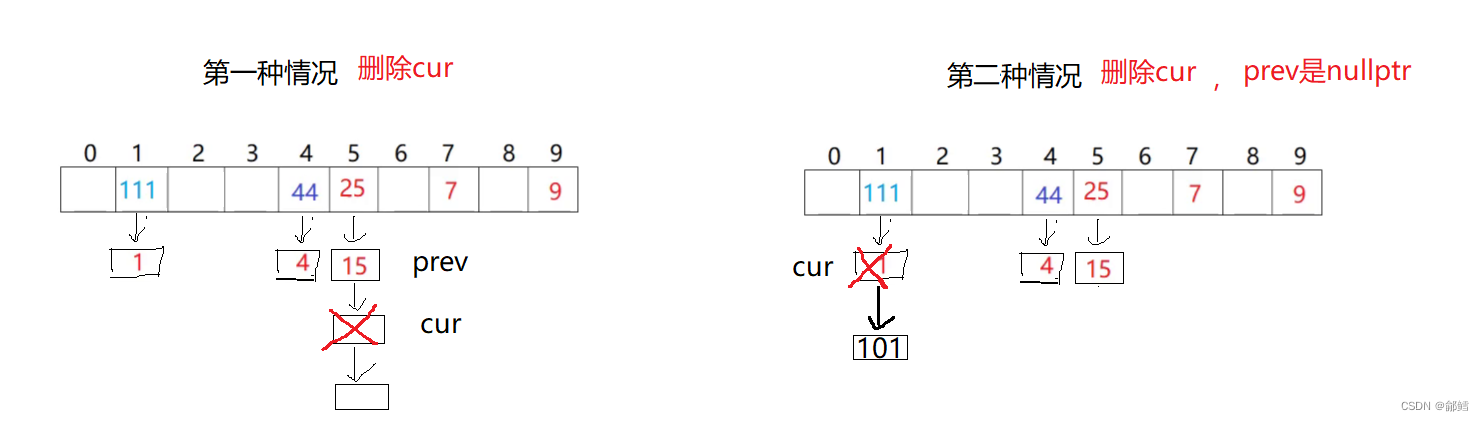
bool Erase(const K & key)
{
size_t hashi = key % _table.size();
Node* cur = _table[hashi];
Node* prev = nullptr;
while (cur != nullptr)
{
if (key == cur->_kv.first)
{
if(prev==nullptr)//第二种情况 ,prev是nullptr ,就是头删
{
_table[hashi] = cur->_next;
}
else//第一种情况 ,cur是头节点
{
prev->_next = cur->_next;
}
delete cur;
return true;
}
prev = cur;
cur = cur->_next;
}
//没找到
return false;
}
namespace hash_bucket
{
template <class K ,class V>
struct HashNode
{
pair<K, V> _kv;
HashNode<K,V>* _next;
HashNode( const pair<K, V> & kv)
:_kv(kv)
,_next(nullptr)
{
}
};
template<class K,class V>
class HashTable
{
public:
typedef HashNode<K,V> Node;
//iterator begin()
//{
//}
//iterator end()
//{
//}
//const_iterator begin()
//{
//}
//const_iterator end()
//{
//}
//GetNextPrime()
//{
//}
HashTable()
{
_table.resize(10, nullptr);
}
~HashTable()
{
}
//bool Insert(const pair<K, V> kv)
//{
// //负载因子到1就扩容
// if (_n == _table.size())
// {
// size_t newsize = _table.size() * 2;
// vector<Node*> newtable;
// newtable.resize(newsize, nullptr);
// }
// size_t hashi = kv.first % _table.size();
// //头插
// Node* newnode = new Node(key);
// newnode->_next = _table[hashi];
// _table[hashi] = newnode;
// ++_n;
// return true;
//}
bool Insert(const pair<K,V> & kv)
{
size_t hashi = kv.first % _table.size();
//负载因子到1就扩容
if (_n == _table.size())
{
size_t newsize = _table.size() * 2;
vector<Node*> newTable;
newTable.resize(newsize, nullptr);
//遍历旧表,将原哈希表当中的结点插入到新哈希表
for (int i = 0; i <= _table.size(); i++)
{
Node* cur = _table[i];
//插入到新哈希表
while (cur != nullptr)
{
Node* next = cur->_next;
// 重新分配hashi
size_t hashi = cur->_kv.first % _table.size();
cur->_next = newTable[hashi];
newTable[hashi] = cur;
cur = next;
}
}
}
//头插
Node* newnode = new Node(kv);
newnode->_next = _table[hashi];
_table[hashi] = newnode;
return true;
}
Node * Find(const K & key)
{
size_t hashi = key % _table.size();
Node* cur = _table[hashi];
while (cur != nullptr)
{
if (key == cur->_kv.first)
{
return cur;
}
cur = cur->_next;
}
return nullptr;
}
bool Erase(const K & key)
{
size_t hashi = key % _table.size();
Node* cur = _table[hashi];
Node* prev = nullptr;
while (cur != nullptr)
{
if (key == cur->_kv.first)
{
if(prev==nullptr)//第二种情况 ,prev是nullptr ,就是头删
{
_table[hashi] = cur->_next;
}
else//第一种情况 ,cur是头节点
{
prev->_next = cur->_next;
}
delete cur;
return true;
}
prev = cur;
cur = cur->_next;
}
//没找到
return false;
}
void Print()
{
for (size_t i = 0; i < _table.size(); i++)
{
printf("[%d]->", i);
Node* cur = _table[i];
while (cur != nullptr)
{
cout << cur->_kv.first << "->";
cur = cur->_next;
}
printf("NULL\n");
}
cout << endl;
}
private:
vector<Node*> _table;//指针数组
size_t _n = 0;//存储有效数据
};
}
如果你觉得这篇文章对你有帮助,不妨动动手指给点赞收藏加转发,给鄃鳕一个大大的关注
你们的每一次支持都将转化为我前进的动力!!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 数字滤波器的设计
- j1冒个泡-排序的演变--扩展题
- CTF-PWN-栈溢出-中级ROP-【栈迁移】
- 有什么好用的C/C++源代码混淆工具?
- 【MySQL】数据库之索引的增删改查
- Dockerfile与DockerCompose
- 算法设计与分析复习笔记第二章递归与分治
- Unity升级到2022版本后,打开Spine会卡住
- 如何在Android Termux中使用SFTP实现远程传输文件
- Arduino开发实例-AS608光学指纹传感器驱动