Python实现多元线性回归模型信用卡客户价值预测项目源码+数据+项目设计报告
发布时间:2023年12月20日
多元线性回归——信用卡客户价值预测
一、背景
这里以信用卡客户的客户价值为例来解释客户价值预测的具体含义:
客户价值预测就是指预测客户在未来一段时间内能带来多少利润,其利润可能来自信用卡的年费、取现手续费、分期手续费、境外交易手续费等。分析出客户价值后,在进行营销、电话接听、催收、产品咨询等各项业务时,就可以针对高价值客户提供区别于普通客户的服务,以进一步挖掘这些高价值客户的价值,并提高他们的忠诚度。
二、数据
- “客户价值”列为在1年里能给银行带来的收益;
- “学历”列的数据已经做了预处理,其中
- 2代表高中及以下学历
- 3代表本科及以上学历
- “性别”列中,0 代表女,1 代表男
部分数据如下:
| 客户价值 | 历史贷款金额 | 贷款次数 | 学历 | 月收入 | 性别 |
|---|---|---|---|---|---|
| 1096 | 6253 | 2 | 2 | 10567 | 0 |
| 1558 | 4779 | 3 | 2 | 10217 | 1 |
| 1681 | 7752 | 3 | 3 | 10317 | 1 |
| 1037 | 5231 | 3 | 2 | 9667 | 1 |
| 1333 | 5485 | 2 | 3 | 10567 | 0 |
三、代码实现
1、导入Python库,引入所需的功能和模块。
import matplotlib.pyplot as plt # 用于绘制数据可视化图形,例如折线图、散点图等
import pandas as pd # 用于数据处理和分析,提供了高效的数据结构和数据操作功能
import statsmodels.api as sm # 用于执行统计模型的拟合和推断,包括回归分析、时间序列分析等
from sklearn.linear_model import LinearRegression # 用于进行线性回归建模和预测
from sklearn.model_selection import train_test_split # 将数据集分割为训练集和测试集,常用于机器学习中的模型评估和验证
2、读取数据
data = pd.read_excel(file_path) # 使用pd.read_excel()函数读取名为'客户价值数据表.xlsx'的Excel文件,并将其存储在data变量中
# 根据指定的测试集比例(这里是20%)将数据分割为训练集和测试集,并且设置了一个随机种子(这里是42)以确保结果可复现
train_data, test_data = train_test_split(data, test_size=0.2, random_state=42)
X = data[['历史贷款金额', '贷款次数', '学历', '月收入', '性别']] # 从data中选取'历史贷款金额'、'贷款次数'、'学历'、'月收入'、'性别'这几列作为自变量,并将其存储在X变量中
Y = data['客户价值'] # 从data中选取'客户价值'这一列作为因变量,并将其存储在Y变量中
X_test = test_data[['历史贷款金额', '贷款次数', '学历', '月收入', '性别']]
Y_test = test_data['客户价值']
3、搭建多元线性回归模型
Regress = LinearRegression() # 创建一个LinearRegression对象,并将其存储在Regress变量中
Regress.fit(X, Y) # 使用X和Y进行线性回归拟合,得到回归模型
Predict = Regress.predict(X) # 对五个特征变量进行回归预测
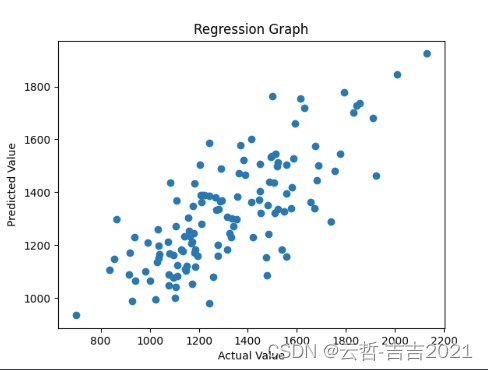
# 2.1绘制真实值和与预测值的散点图形
plt.scatter(Y, Predict)
# 2.2设置图例
plt.xlabel('Actual Value')
plt.ylabel('Predicted Value')
plt.title('Regression Graph')
plt.show() # 显示
真实值和与预测值的散点图形
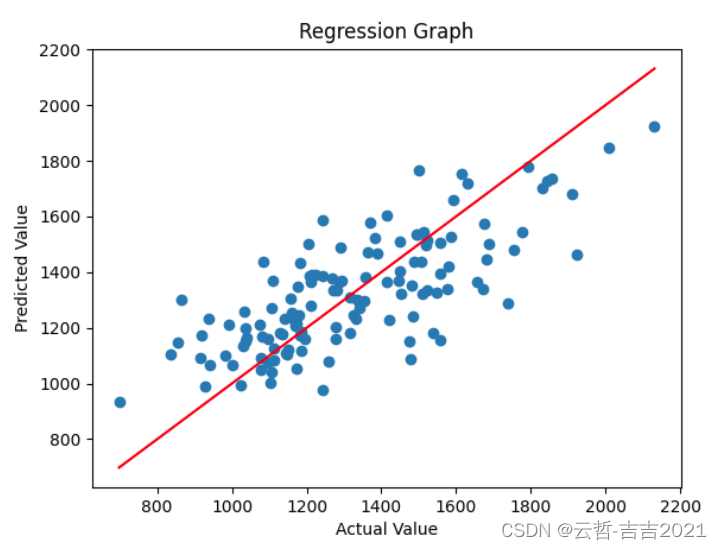
添加一条拟合线
plt.plot([Y.min(), Y.max()], [Y.min(), Y.max()], 'r-')
4、构造多元线性回归方程表达式
K = Regress.coef_
b = Regress.intercept_
print('各斜率系数为:\n', str(K)) # 打印输出回归模型的各系数值
print('常数项系数k0(截距)为:\n', str(b)) # 打印输出回归模型的常数项系数k0
expression = construct_expression(K, b) # 计算多元线性回归方程函数表达式
print("多元线性回归方程为:\n", expression)
各斜率系数为:
[5.71421731e-02 9.61723492e+01 1.13452022e+02 5.61326459e-02 1.97874093e+00]
常数项系数k0(截距)为:
-208.42004079958429
多元线性回归方程为:
Y = -208 + 0.057X1 + 96X2 + 113X3 + 0.056X4 + 1.98X5
5、模型评估
X1 = sm.add_constant(X) # 在X变量中添加常数列,并将新的X变量存储在X1中
est = sm.OLS(Y, X1).fit() # 使用OLS方法进行普通最小二乘回归拟合,得到回归模型的估计值,将结果存储在est变量中
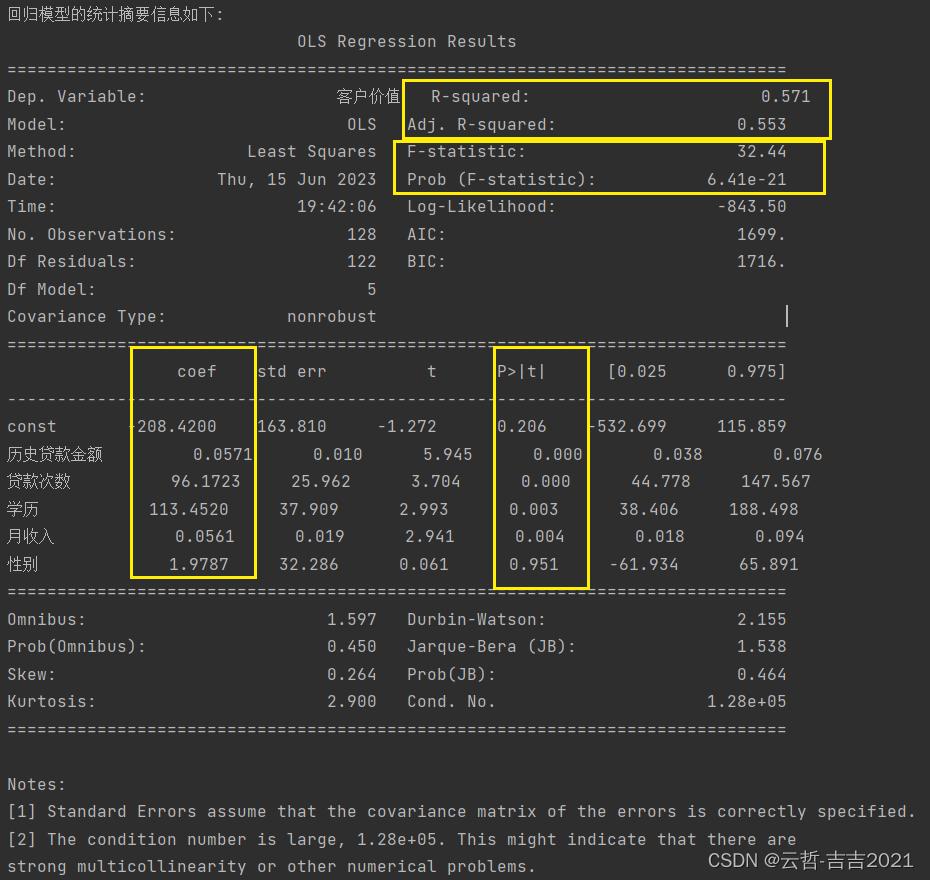
print('\n\n回归模型的统计摘要信息如下:\n', est.summary()) # 输出回归模型的统计摘要信息
运行输出如下:可以看到,模型的R-squared值为0.571,Adj.R-squared值为0.553,整体拟合效果不是特别好,可能是因为本案例的数据量偏少,不过在此数据量条件下也算可以接受的结果。再来观察P值,可以发现大部分特征变量的P值都较小,的确与目标变量(即“客户价值”)显著相关,而“性别”这一特征变量的P值达到了0.951,即与目标变量没有显著相关性,这个结论也符合经验认知,因此,在之后的建模中可以舍去“性别”这一特征变量
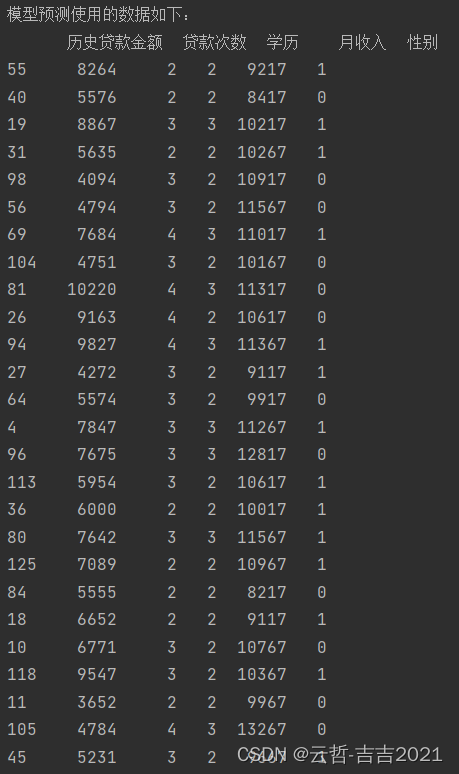
6、模型预测
predict_new_data(Regress, X_test, Y_test)
运行输出如下:
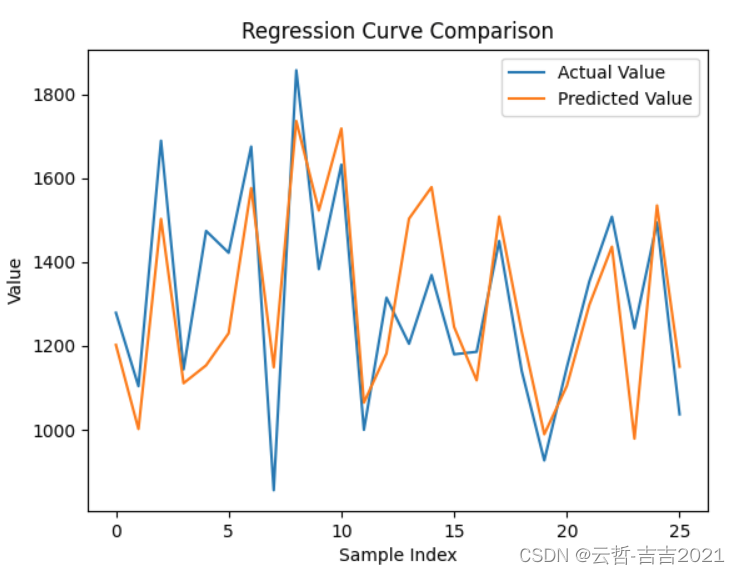
真实值与预测值对比图
7、相关函数
# 构造函数表达式
# 表达式中的系数值在-1到1之间的要保留三位小数,系数值在-10到-1以及1到10之间的要保留两位小数,其余保留整数
def construct_expression(K, b):
expression = f"Y = {int(b)}"
for i, coef in enumerate(K):
if -10 <= coef <= -1 or 1 <= coef <= 10:
expression += f" + {coef:.2f}*X{i + 1}"
elif -1 <= coef <= 1:
expression += f" + {coef:.3f}*X{i + 1}"
else:
expression += f" + {int(coef)}*X{i + 1}"
return expression
# 模型预测
def predict_new_data(model, X_new, Y_new):
print("\n\n\n\n模型预测使用的数据如下:\n", X_new)
new_prediction = model.predict(X_new)
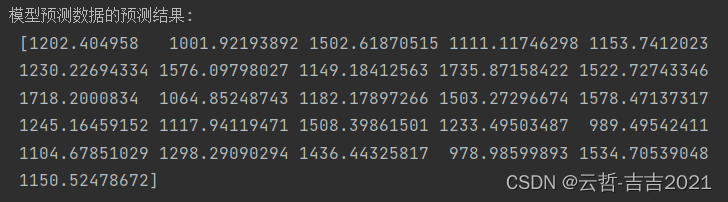
print('模型预测数据的预测结果:\n', new_prediction)
# 绘制真实值与预测值对比图
plt.plot(Y_new['客户价值'].tolist(), label='Actual Value')
plt.plot(new_prediction, label='Predicted Value')
plt.xlabel('Sample Index')
plt.ylabel('Value')
plt.title('Regression Curve Comparison')
plt.legend()
plt.show()
8、程序入口
# 程序入口
if __name__ == '__main__':
path = '客户价值数据表.xlsx'
multiple_linear_regression(path) # 调用函数并传入数据文件的路径
完整代码下载地址:Python实现多元线性回归模型信用卡客户价值预测
文章来源:https://blog.csdn.net/shiyunzhe2021/article/details/135113986
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- “揭秘性能测试工具:优化软件性能的关键秘籍“
- Redis原理篇(List底层结构与源码详解)
- 基于SpringBoot+Redis的前后端分离外卖项目-苍穹外卖微信小程序端(十二)
- 【C/C++】轻量级跨平台 开源串口库 CSerialPort
- Unity中Shader面片一直面向摄像机(个性化修改及适配BRP)
- java---变量
- Hello,World!
- 采集小红书笔记详情页的方法,大部分人都想得复杂了
- 迅为RK3568开发板助力智能车载产业快速发展
- ICV:2023 年人工智能芯片市场研究报告