基于python的leetcode算法介绍之动态规划

零 算法介绍

动态规划（Dynamic Programming，DP）是一种解决最优化问题的算法思想，通过将问题分解成更小的子问题来解决。其核心思想是将一个问题分解成更小的、相互独立的子问题，然后将子问题的解组合起来，形成原问题的解。但与之前的算法不一样的是，动态规划强调的是动态的过程，即在程序计算时，会出现随程序运行而变化的参数辅助程序完成算法计算。

动态规划算法的主要特点包括：

1. 重叠子问题：动态规划算法解决的问题通常包含许多重叠的子问题。

2. 状态转移方程：动态规划算法通常使用状态转移方程来描述问题的状态和状态转移关系。

3. 自底向上：动态规划算法通常采用自底向上的方法，即从最小的子问题开始解决，逐步解决更大的子问题。

动态规划算法的应用范围非常广泛，包括：

1. 组合优化问题：如背包问题、旅行商问题等。

2. 序列问题：如最长公共子序列、最长递增子序列等。

3. 图论问题：如最短路径问题、最小生成树问题等。

4. 动态规划在游戏、人工智能、计算机图形学等领域也有广泛应用。

动态规划算法有很多变种，如线性动态规划、树形动态规划、网格动态规划等。在实际应用中，需要根据问题的特点选择合适的动态规划算法。

一 例题介绍 使用最小花费爬楼梯

给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。

你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

请你计算并返回达到楼梯顶部的最低花费。

示例 1：

输入：cost = [10,15,20]
输出：15
解释：你将从下标为 1 的台阶开始。
- 支付 15 ，向上爬两个台阶，到达楼梯顶部。
总花费为 15 。

问题分析

动态规划强调的是动态的过程， 故当我们再看这道题目的时候，我们的关注点是 一旦你支付此费用，即可选择向上爬一个或者两个台阶。 当我们转换一下思路，则是：当前台阶的价值应该是由前一个台阶或是前前一个台阶决定的。如果这套规则适用的话，则代表第N阶的台阶等于total[n] = min(total[n-1]+cost[n-1], total[n-2]+cost[n-2])。即，当前台阶的最低花费应该是在上两级台阶的最小开销中进行选择。

代码呈现如下：

class Solution:
    def minCostClimbingStairs(self, cost: List[int]) -> int:
        old1, old2 = 0, 0     # 初始化前前一个台阶和前一个台阶的初始价格
        for i in cost:        # 对所有台阶遍历
            temp = i + min(old1, old2)     # 第N个台阶的花费是当前第N个台阶的价格加上前两级台阶中小的那个
            old1, old2 = old2, temp        # 迭代
        return min(old1, old2)

Leetcode例题与思路

接下来，我们列举关于Leetcode的几道例题，并通过动态规划的方式进行求解：

118. 杨辉三角

给定一个非负整数 *numRows，*生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

        1
       1 1
      1 2 1
     1 3 3 1
    1 4 6 4 1

解题思路

这道题目是最简单的动态规划题目，对于第N行来说，其第1个和最后一个应当为1，其余位置可以通过上一行中当前位置和当前位置的下一位置两个元素求和完成。转换成代码如下所示：

题解

class Solution:
    def generate(self, numRows: int) -> List[List[int]]:
        res = []
        for i in range(numRows):
            row = [None for _ in range(i + 1)]
            row[0], row[-1] = 1, 1
            for j in range(1, len(row) - 1):
                row[j] = res[i - 1][j - 1] + res[i - 1][j]
            res.append(row)
        return res

53. 最大子数组和

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

解题思路

由于这边仅需要找到最大和，无需判断位置。故我们仅需判断最大值作为我们的判断。那么最大子数组和应该有什么特点呢？其实从这道题目中我们就会发现从哪开始到哪结束是不重要的。需要关注的是在第N个元素的位置，我们之前的元素和大于零还是小于零。什么意思呢？即之前元素之和如果小于0，那么对于后续元素求和只有负面效果，故可以直接丢弃从第N个元素开始重新统计。而我们只需要在这个过程中，找到累计和最大的值就可以了。由题目的提示可知，-10^4 <= nums[i] <= 10^4。故我们可以选择-10000作为初始化：

题解

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        temp, max_value = -10000, -10000
        for i in nums:
            temp = max(temp + i, i)
            max_value = max(temp, max_value)
        return max_value

96. 不同的二叉搜索树

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：

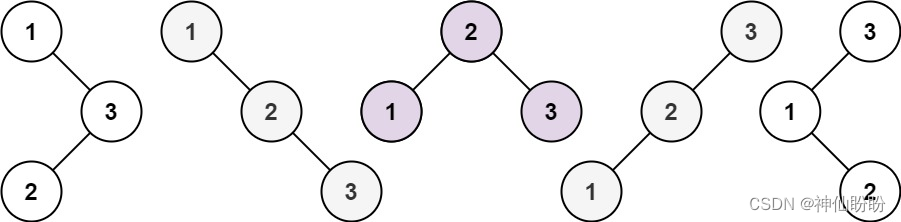
解题思路

首先我们需要明确一个概念，什么是二叉搜索树：

二叉搜索树（Binary Search Tree, BST）是一种特殊的二叉树，它的每个节点都有一个关键值，并且所有节点的关键值满足以下性质：

1. 节点的左子树（如果存在）的关键值都小于节点的关键值。

2. 节点的右子树（如果存在）的关键值都大于节点的关键值。

3. 节点的左右子树（如果存在）也都是二叉搜索树。

这种结构使得二叉搜索树在查找、插入和删除操作方面具有较高的效率。

那么面对这样一道题，我们该如何求解呢？首先，我们需要明确一个问题，就是对于N个节点的二叉树，我们可以把这个二叉树从节点切分，分为成小于该长度的二叉树来求解。换句话说，我们在面对一个4节点的二叉搜索树，可以看作013[代表左子树0，根节点1，右节点3]，112, 211 , 310。所以我们仅需要得到1节点，2节点和3节点的树就可以推出4节点的数量。那么我们可以快速推出，0节点仅存在1种排列，1节点仅存在1种排列。从2节点开始，我们可以通过公式进行推理：N节点的树可以看作N个根和他们的左右子树。故，我们可以通过左子树的种类乘以右子树的种类得到每个节点存在子树的个数。继续以4节点树为例，可以分为013，112, 211 , 310。当我们知道0，1，2，3个节点的数量时，就可以得到013[1*5]，112[1*2], 211[2*1] , 310[5*1]。故四节点可以构建5+2+2+5=14个排列。

题解

class Solution:
    def numTrees(self, n: int) -> int:
        node_list = [1 for i in range(0, n+1)]
        for i in range(2, n+1):
            node_list[i] = sum([node_list[j] * node_list[i-j-1] for j in range(i)])
        return node_list[-1]

322. 零钱兑换

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

解题思路

这道题目可以转换成走楼梯的思路。如果还不能get到这个思路的话，我们再细说一下：

针对N块钱，凑出来的方法必然是考虑N块钱前一步的状态，即N块钱减去coins的状态下需要多少步。所以我们从coins最小的储蓄开始执行，通过对比上一步的所有状态，选择其中需要部署最小的作为自己的结果，一直到amount，得到最终结果。

题解

class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        answer = [-1 for i in range(amount+1)]             # 初始化所有状态
        answer[0] = 0                                      # 初始化0，这样coins中的所有元素的步长都为1
        for i in range(min(coins), amount+1):              # 计算到amount的步长
            mins = 2**31
            for j in coins:                                # 对比coins中的所有状态
                if i - j >= 0 and answer[i - j] > -1:      # 当上一状态合法且存在时，获得最小步数
                    mins = min(answer[i - j] + 1, mins)
            answer[i] = mins if mins != 2**31 else -1      # 更新当前状态
        return answer[-1]

124. 二叉树中的最大路径和

二叉树中的 路径 被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

解题思路

这是一道将动态规划运用到树上的一道题，结合了树的搜索，故还需要用到递归的方法进行搜索。

我们对其中任意节点进行思考，如何判断当前节点以下的树节点应当被省略？即会降低全局解的情况，也就是当前节点联通的路径小于0的情况下。那怎么得到当前节点的联通路径呢？即根节点和左子树与右子树中较大的值的和。故我们需要注意，**左子树和右子树的返回结果是必然大于0的，否则就没有链接的必要。**那如果不回调的话，最大联通树应该是当前节点加上左节点加上右节点的值，如果当前值大于已知的最大值，那么就可以替换当前的最大值。

题解

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxPathSum(self, root: Optional[TreeNode]) -> int:
        self.answer = -1000
        self.maxroot(root)
        return self.answer

    def maxroot(self, root):
        if root == None:
            return 0
        else:
            left = self.maxroot(root.left)
            right = self.maxroot(root.right)
            self.answer = max(self.answer, root.val + left + right)
            return max(max(left, right) + root.val, 0)

以上就是最基础的动态规划，动态规划的题目难度非常大，后续有精力会详细拆开，深入剖析。