python不同方法求完全平方数问题

问题描述主要是给定一个正整数，需要找出该整数至少可以由几个完全平方数累加所组成的，这里的完全平方数是指整数的平方，例如4,16,9等，都是完全平方数。

例如给定一个15整数，输出的是4，这里的的累加的完全平方数是1、1、4、9

添加图片注释，不超过 140 字（可选）

同样的例如输入的是一个3，则最少得由三个完全平方数1来累加成为该整数。

对于该问题，主要是先将题目考虑为一个从根节点0到叶子结点n的过程，逐层向下累加，直到累加之和为n即结束，此时的树的深度就是想要求的值也就是完全平方数的个数，而且每一次叠加的过程都必须是一个完全平方数。

这里需要注意一个问题，当给定的正整数为n的时候，则能够作为选择的完全平方数的范围是指定的，也就是1到n的开方取整，这两个数据之间的值，例如当n时13的时候，则13开方并取整的值为3，则针对输入时13这个时候的时候，每一层可累加的数据只能从1、4、9之间进行选择，这也就从搜索范围内进行了缩小，也就提高了效率。由于所需要的最后的结果是完全平方数的个数，也就是最后那个节点所在的深度，因此也就可以在每个节点上再定义一个变量来代表这个节点的深度，也就是如下图的一颗二叉树。

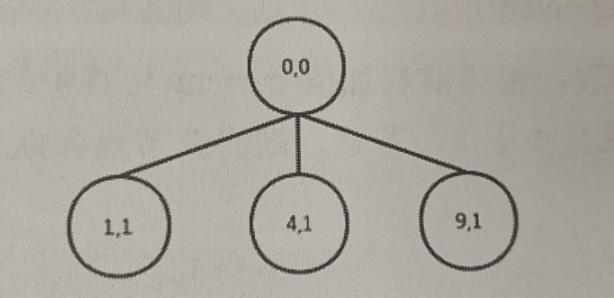
添加图片注释，不超过 140 字（可选）

在遍历的过程中对每个节点执行相同的奥做，如果想要减少重复的计算，则应该将已经出现过的累加之和保存在一个集合中，这样若此次累加得到的和已经出现过了，就不再记录这个节点了，过程演示如下：

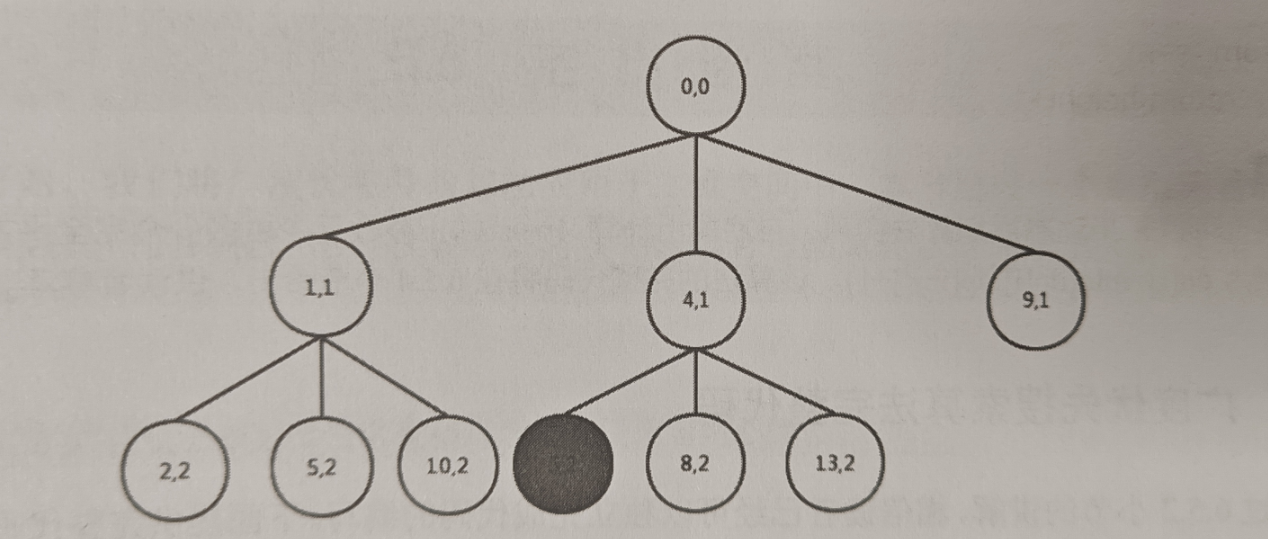
添加图片注释，不超过 140 字（可选）

直到累加值为n的时候，就停止继续，返回的深度值即为所需要的结果，这样的一个过程使用的也就是广度优先搜索算法的思路。广度优先搜索算法的代码如下：

from collections import deque
def square(n):
    selected=[i**2 for i in range(1,int(n**0.5)+1)]
    visited = set()
    queue=deque([(0,0)])
    while(queue):
        current,height=queue.popleft()
        for i in selected:
            sum_= current+i
            if sum_==n:
                return height+1
            if sum_<n and sum_ not in visited:
                visited.add(sum_)
                queue.append((sum_,height+1))

这里还提供了其他的方法来解决这个问题，使用动态规划算法来实现的代码实现：

def square(n):
    dp=[i for i in range(n+1)]
    for i in range(4,n+1):
        for j in range(int(n**0.5),0,-1):
            if i>=j**2:
                dp[i]=min(dp[i],dp[i-j*j]+1)
    return dp[n]