LLM：Scaling Laws for Neural Language Models 理解

发布时间：2024年01月15日

核心结论

1：LLM模型的性能主要与计算量C，模型参数量N和数据大小D三者相关，而与模型的具体结构 (层数/深度/宽度) 基本无关。三者满足:??C ≈ 6ND

2. 为了提升模型性能，模型参数量N和数据大小D需要同步放大，但模型和数据分别放大的比例还存在争议。

核心公式：本部分来自参考2.

  • 第一项L_{\infty }是指无法通过增加模型规模来减少的损失，可以认为是数据自身的熵（例如数据中的噪音）
  • 第二项(\frac{x_{0}}{x})^{a}是指能通过增加计算量来减少的损失，可以认为是模型拟合的分布与实际分布之间的差。

根据公式，增大x?(例如计算量C)，模型整体loss下降，模型性能提升；伴随x?(例如计算量C) 趋向于无穷大，模型能拟合数据的真实分布，让第二项逼近0，整体趋向于L_{\infty }

结论验证

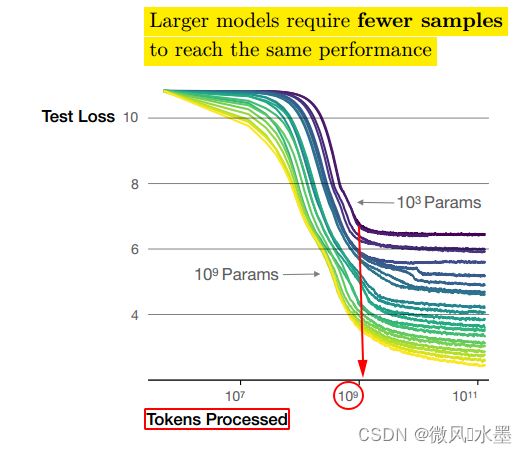
从图上可以看出：

1：当模型的参数量 N 为10^{3}时（图中紫色的线），在 Token 数量达到 10^{9}后（图中红色的圈），模型基本收敛，继续增加训练的 Token 数量，纵轴的Test Loss 并没有明显下降。

2：如果此时，增加模型的参数量N：10^{3}->10^{9}。?纵轴的Test Loss：从6.x->3.x。可以看出：提升模型参数量带来的收益更大。

测试一下：你对 scale law 的理解程度：基于上图，当模型的参数量 N 为10^{3}时（图中紫色的线），模型收敛需要的算力C，以及耗时呢？

先看实验答案：下图红色箭头指向位置，也就是图中紫色线的拐点。

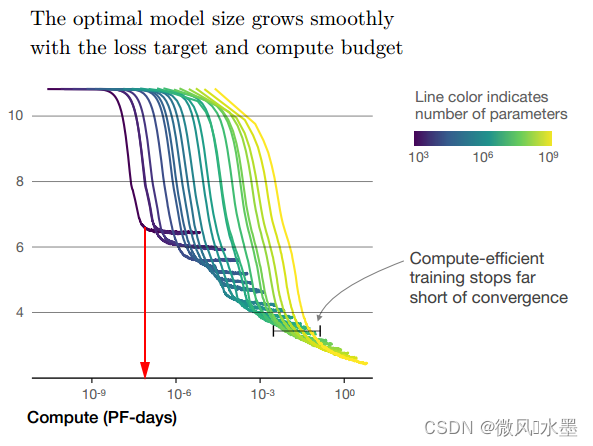
C\approx 6\ast N\ast D\approx 6\ast 10^{3}\ast 10^{9}\approx 6\ast 10^{12}

Compute (PF-days) \approx 7\ast 10^{-8}

如果没做实验，收敛算力和收敛耗时该怎么推算呢？

C\approx 6\ast N\ast D\approx 6\ast 10^{3}\ast 10^{9}\approx 6\ast 10^{12}

Compute(PF-days) = \frac{C}{PF-days}=\frac{6\ast 10^{12}}{8.64\ast 10^{19}}\approx 6.99\ast 10^{-8}=7\ast 10^{-8}

Tips：

PF-days: 如果每秒钟可进行1015次运算，就是1 peta flops，那么一天的运算就是1015×24×3600=8.64×1019，这个算力消耗被称为1个petaflop/s-day。

再看个例子：

下图是Baichuan-2技术报告中的Scaling Law曲线。基于10M到3B的模型在1T数据上训练的性能，可预测出最后7B模型和13B模型在2.6T数据上的性能。

?在1T的数据上，训练的10M-3B的模型，是怎么推算训练7B/13B需要2.6T数据呢？

C\approx 6\ast N\ast D

D\approx \frac{C}{6\ast N}=\frac{10^{23}}{6\ast 7B}=\frac{10^{23}}{6\ast 7\ast 10^{9}}\approx 2.38T

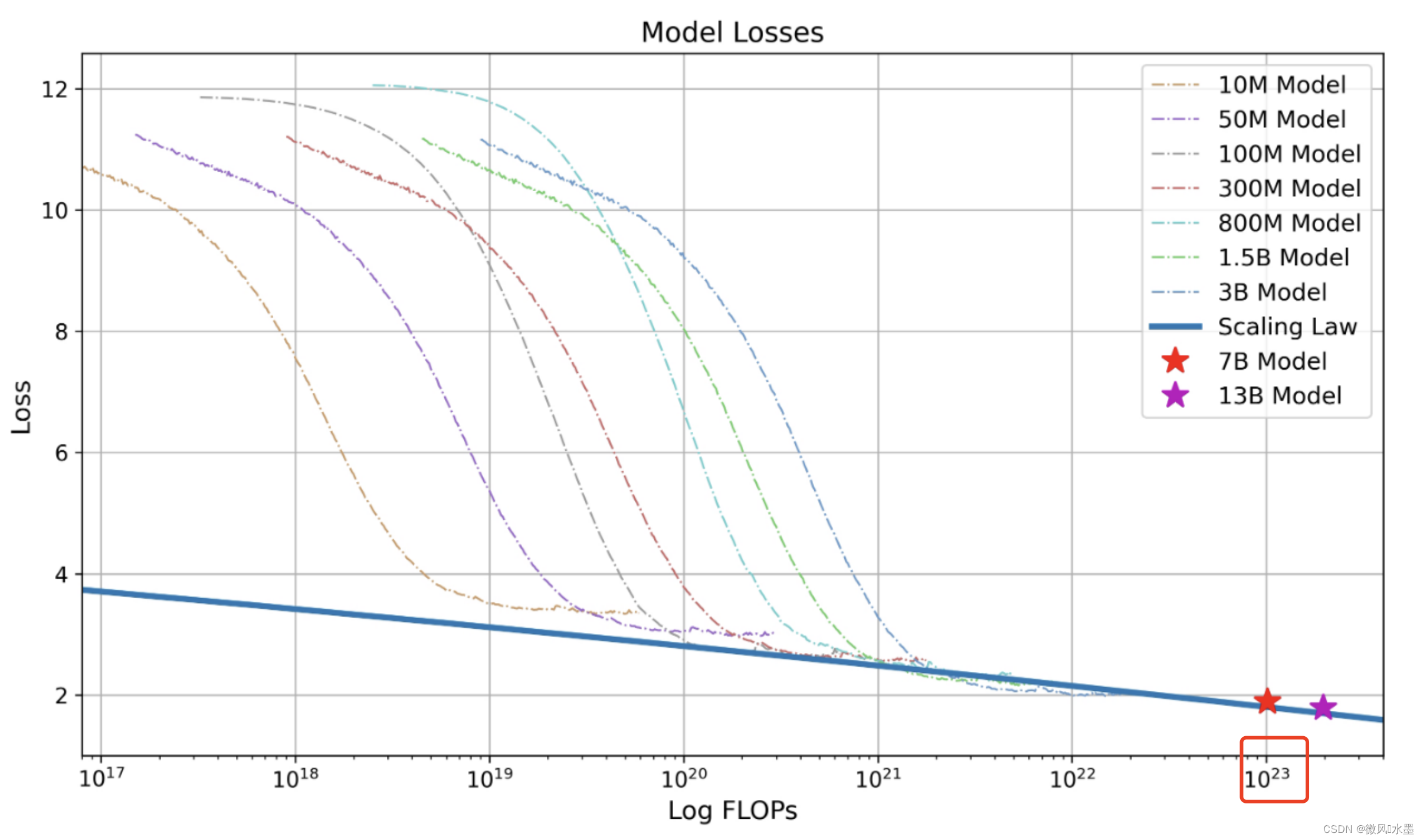
2.38T 是理论数值，与 2.6T基本一致了。

参考

1：介绍一些Scaling Laws - 知乎

2：解析大模型中的Scaling Law - 知乎?

文章来源:https://blog.csdn.net/lilai619/article/details/135601415
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章