【C++】c++排序算法入门之冒泡排序
前言
本章节主要讲述冒泡排序的相关内容。
学习路线:C++从入门到NOI学习路线
学习大纲:C++全国青少年信息学奥林匹克竞赛(NOI)入门级-大纲
上一站:C++算法入门之穷举
下一站:
一、排序及其基本概念
1.1 什么是排序?
假设一个班有n个同学,现在有n个记录,这些记录是全班学生成绩,老师在统计这些数据的时候不可能都按照数据的顺序去统计(因为事先并不知道谁大谁小)。现在老师想要知道学生成绩排列情况,那么就需要将这些记录按照从高到低的顺序排列。

而将杂乱无章的数据元素,通过一定的方法按关键字顺序排列的过程就叫做排序。
1.2 排序算法分析
几乎所有的排序都有两个基本的操作:
(1)关键字大小的比较。
(2)改变记录的位置。具体处理方式依赖于记录的存储形式,对于顺序型记录,一般移动记录本身,例如数组;而链式存储的记录则通过改变指向记录的指针实现重定位,例如链表。
1.3 排序算法性能评价
排序的算法很多,不同的算法有不同的优缺点,没有哪种算法在任何情况下都是最好的。评价一种排序算法好坏的标准主要有两条:
(1)执行时间和所需的辅助空间,即时间复杂度和空间复杂度;
(2)算法本身的复杂程度,比如算法是否易读、是否易于实现。
二、冒泡排序
冒泡排序,作为一种基础且直观的排序算法,在计算机科学与软件工程领域占据着重要的地位。它的名称来源于其运行过程类似于水底下的气泡慢慢升至水面,小元素经过一轮又一轮的比较和交换逐渐“浮”到序列的前面,而大元素则逐步沉降到后面。

2.1 基本思想
冒泡排序的基本思想是通过不断比较相邻两个元素并交换他们的位置(如果需要),使得每一轮遍历后,最大的(或最小的)元素如气泡般逐渐“冒出”。在第一轮中,最大元素会被排至末尾;第二轮则将次大的元素排至倒数第二位,以此类推,直至整个序列有序。
具体实现步骤如下:
- 从数组的第一个元素开始,对相邻的两个元素进行比较。
- 如果前一个元素大于后一个元素,则交换这两个元素的位置。
- 对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对,这样一趟比较结束后,最大的元素会被交换到最后的位置。
- 针对所有未排序的元素重复以上步骤,除了最后一个(因为它已经是最大值了)。
- 持续进行上述过程,直到没有任何一对数字需要比较和交换位置,即完成排序。
尽管冒泡排序简单易懂,但其时间复杂度为O(n^2),在处理大规模数据时效率较低,不适用于对效率要求较高的场景。
虽然冒泡排序不是最优解,却为我们理解排序算法的核心逻辑提供了清晰的示例,其原理在各种高级排序算法的设计中亦有体现,对于编程初学者及算法研究者具有不可忽视的学习意义。
2.2 排序过程
现在有10个数,如下图所示。可以看到这些数的排列顺序并没有按照它们实际的大小进行排列,接下来将通过冒泡排序将这些数重新排列。

假设这是10个有重量的气泡,它的重量就是它的数值。它是竖直于水中的。

那么根据重量来说,轻的气泡(数值小)肯定在重的气泡上方。那我们从上向下扫描所有数据,凡是违反了这个规则的气泡都使其向上"漂浮"。


以上的两张图片就是我们按照规则(轻的气泡(数值小)在重的气泡上方)对10个数字进行了一次扫描(两两比较),如果违反了这个规则的气泡都使其向上"漂浮"。

从上面对比可以发现,我们找到了这些数中的最大数97,并且将它放到了末尾。这意味着我们下次扫描可以不用管最后一个数。
我们接着扫描。
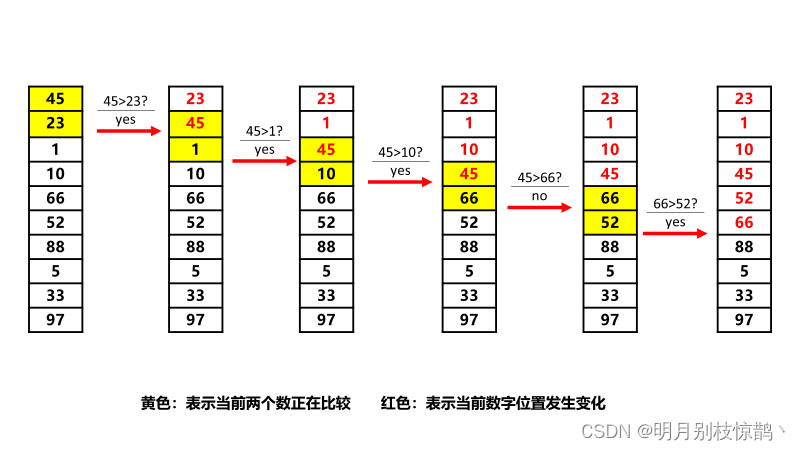

通过第二轮对比,我们找到了第二大的数88。

我们接着从上向下扫描,这次可以跳过末尾两个数。
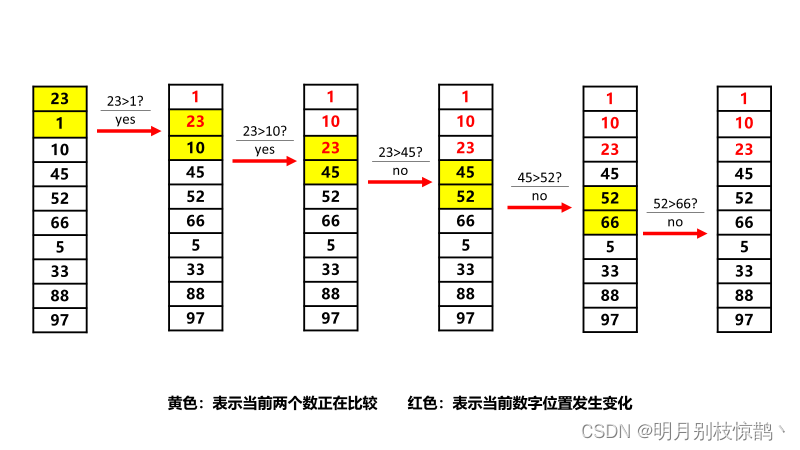
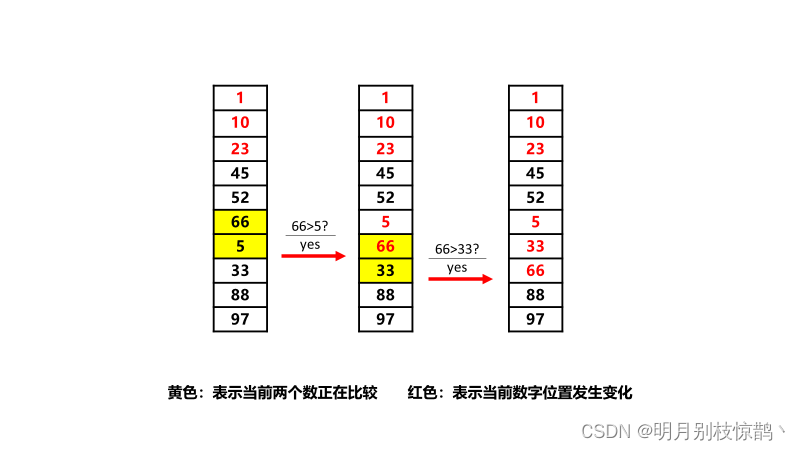
通过第三轮对比,我们找到了第三大的数66。

那么一直重复这个工作…

好,我们直接来看最后结果。相信以你们的聪明才智,能够脑补跳过的环节。
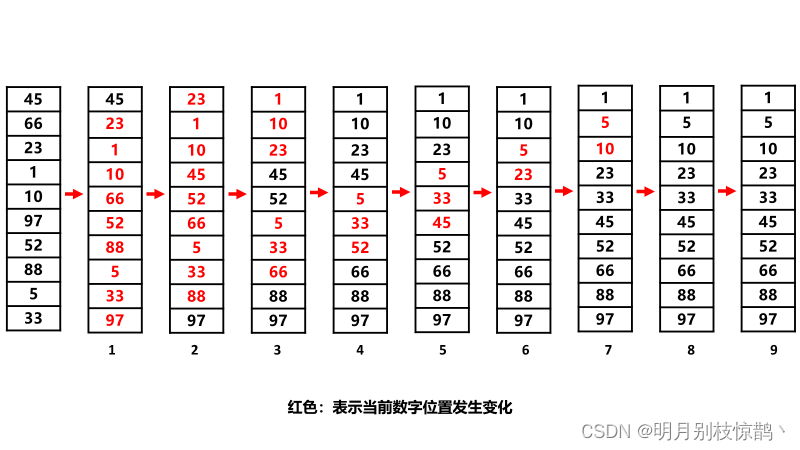
可以看到,经过9次操作,我们终于将原本杂乱的数据给按顺序分布。
路人:第7次和第8,9次没有变化啊,是不是多进行了一些无意义的操作。

这是因为每一轮要确保一个最大的元素被正确地放到它最终的位置上(即数组的末尾)。
第7次和第8次结果一致只是因为5刚好比1小,如果5变成0,那么它们的结果还一样吗?
根据上面的图片演示的冒泡排序过程,相信各位已经掌握了这门武功,甚至迫不及待地想要打怪升级了。别着急,我们先来学习一下“心法”。
在C++中,冒泡排序的基本实现如下:
// 外层循环控制遍历轮数,共需 n-1 轮来确保序列有序
for (int i = 0; i < n - 1; i++) {
// 内层循环控制每轮遍历时的元素比较和交换
for (int j = 0; j < n - 1 - i; j++) {
// 如果当前元素比下一个元素大,则交换它们的位置
if (arr[j] > arr[j + 1]) {
swap(arr[j], arr[j + 1]);
}
}
}
为什么外层循环次数是i < n - 1,内层循环次数是n - 1 - i?
比如我们上面有10个数,对包含10个数的数组进行完全排序时,理论上最多需要进行9轮比较和交换操作。(i = 0,1,2,3,4,5,6,7,8)
具体次数如下:
第一轮:比较并可能交换9次
第二轮:比较并可能交换8次
…
第九轮:比较并可能交换1次
那我们用上面的“心法”,完成我们举的例子。
代码实现如下:
#include<bits/stdc++.h>
using namespace std;
int main(){
int a[10]={45,66,23,1,10,97,52,88,5,33};
//显示原数组顺序
for(int i=0;i<10;i++){
cout<<a[i]<<" ";
}
//冒泡排序
for(int i=0;i<10-1;i++){
for(int j=0;j<10-i-1;j++){
int t;
if(a[j]>a[j+1]){
t=a[j];
a[j]=a[j+1];
a[j+1]=t;
}
}
}
cout<<endl;
//更新后数组顺序
for(int i=0;i<10;i++){
cout<<a[i]<<" ";
}
return 0;
}
三、例题讲解
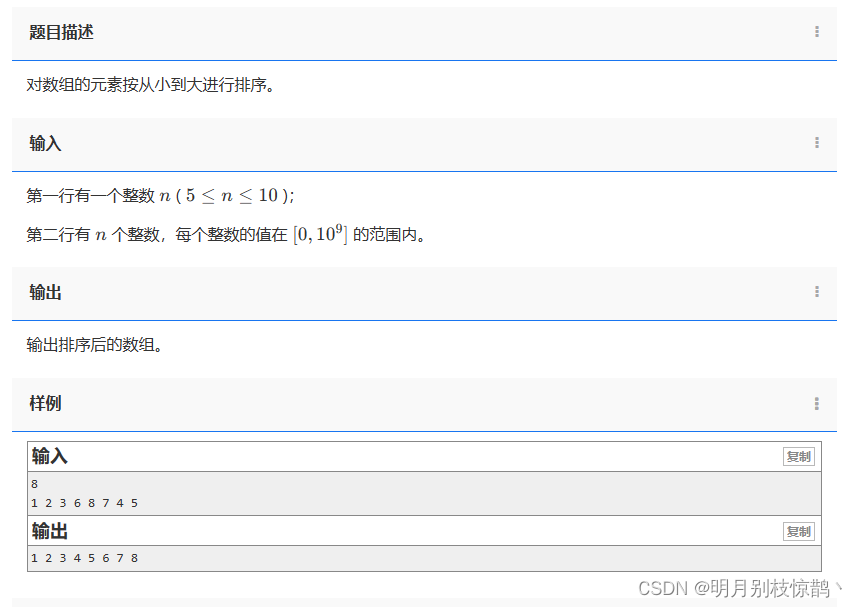
问题一:1010 - 数组元素的排序
对数组的元素按从小到大进行排序。
1.分析问题
- 已知:n个整数的数组
- 未知:更新后的数组
- 关系:从小到大进行排序-冒泡排序
2.定义变量
根据分析的已知,未知按需要定义变量。
//二、数据定义
int n,arr[10];
3.输入数据
从键盘读入。
//三、数据输入
cin>>n;
for(int i=0;i<n;i++){
cin>>arr[i];
}
4.数据计算
//四、数据计算
//排序1:冒泡
for(int i=0;i<n-1;i++) {
for(int j=0;j<n-1-i;j++){
if(arr[j]>arr[j+1]){
int temp;
temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
}
5.输出结果
#include<iostream>
using namespace std;
int main(){
//一、分析问题
//已知:n个整数的数组
//未知:更新后的数组
//关系:从小到大进行排序-冒泡排序
//二、数据定义
int n,arr[10];
//三、数据输入
cin>>n;
for(int i=0;i<n;i++){
cin>>arr[i];
}
//四、数据计算
//排序1:冒泡
for(int i=0;i<n-1;i++) {
for(int j=0;j<n-1-i;j++){
if(arr[j]>arr[j+1]){
int temp;
temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
}
//五、输出结果
for(int i=0;i<n;i++){
cout<<arr[i]<<" ";
}
return 0;
}
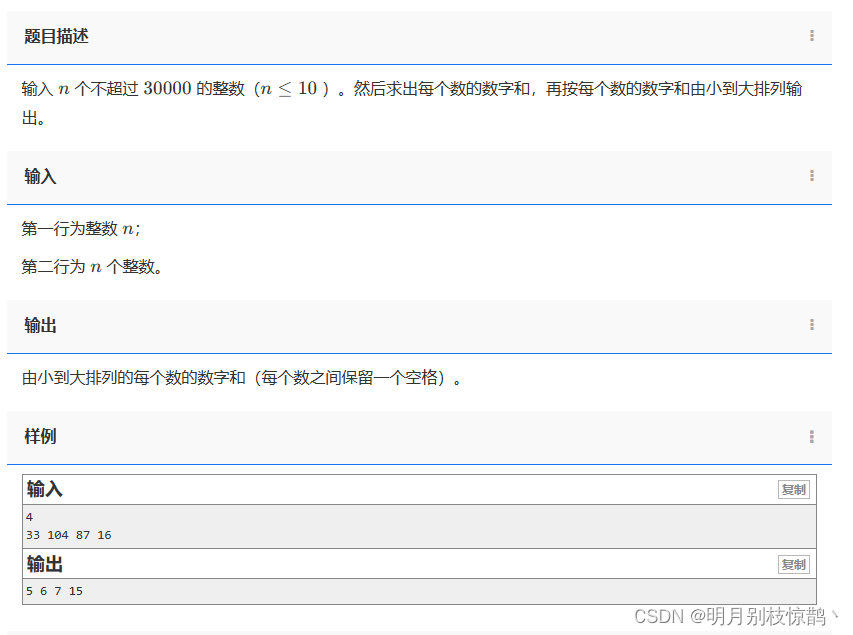
问题二:1166 - 数的排序
输入 n 个不超过 30000 的整数(n≤10 )。然后求出每个数的数字和,再按每个数的数字和由小到大排列输出。
1.分析问题
- 已知:n个不超过30000的整数的数组
- 未知:更新后的数组
- 关系:从小到大排列的每个数的数位和
2.定义变量
根据分析的已知,未知按需要定义变量。
sum:和。
//二、数据定义
int n,a[20],sum;
3.输入数据
从键盘读入。
每个数字的数位和,因此使用短除法获得各位余数。
//三、数据输入
cin>>n;
for(int i=0;i<n;i++){
cin>>a[i];
sum=0;
while(a[i]>0){
sum+=a[i]%10;
a[i]/=10;
}
a[i]=sum;
}
4.数据计算
冒泡排序。
//四、数据计算
for(int i=0;i<n-1;i++){
for(int j=0;j<n-i-1;j++){
int temp;
if(a[j]>a[j+1]){
temp=a[j+1];
a[j+1]=a[j];
a[j]=temp;
}
}
}
5.输出结果
#include<iostream>
using namespace std;
int main(){
//一、分析问题
//已知:n个不超过30000的整数的数组
//未知:更新后的数组
//关系:从小到大排列的每个数的数位和
//二、数据定义
int n,a[20],sum;
//三、数据输入
cin>>n;
for(int i=0;i<n;i++){
cin>>a[i];
sum=0;
while(a[i]>0){
sum+=a[i]%10;
a[i]/=10;
}
a[i]=sum;
}
//四、数据计算
for(int i=0;i<n-1;i++){
for(int j=0;j<n-i-1;j++){
int temp;
if(a[j]>a[j+1]){
temp=a[j+1];
a[j+1]=a[j];
a[j]=temp;
}
}
}
//五、输出结果
for(int i=0;i<n;i++){
cout<<a[i]<<" ";
}
return 0;
}
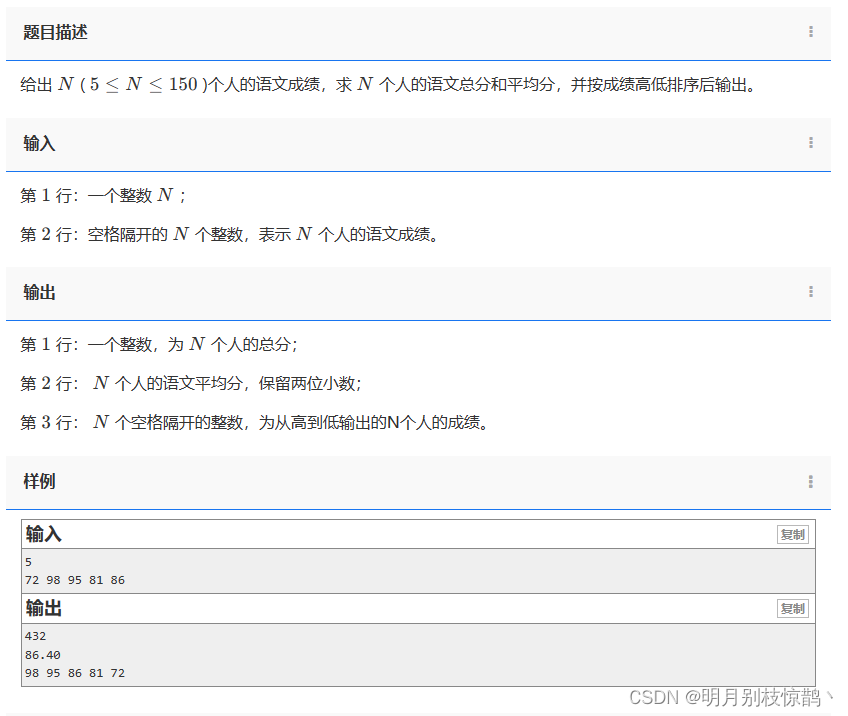
问题三:1175 - 语文成绩
给出 N (5≤N≤150 )个人的语文成绩,求 N 个人的语文总分和平均分,并按成绩高低排序后输出。
1.分析问题
- 已知:N个人的语文成绩
- 未知:总分sum 平均分avg 排名顺序
- 关系:顺序从高到低
2.定义变量
根据分析的已知,未知按需要定义变量。
//二、数据定义
int n,a[200],sum=0;
double avg=0;
3.输入数据
从键盘读入。
//三、数据输入
cin>>n;
for(int i=0;i<n;i++){
cin>>a[i];
sum+=a[i];
}
4.数据计算
冒泡排序,注意是从高到低排列。
//四、数据计算
avg=sum*1.0/n;
for(int i=0;i<n-1;i++){
for(int j=0;j<n-i-1;j++){
int temp;
if(a[j]<a[j+1]){
temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
}
5.输出结果
#include<iostream>
using namespace std;
int main(){
//一、分析问题
//已知:N个人的语文成绩
//未知:总分sum 平均分avg 排名顺序
//关系:顺序从高到低
//二、数据定义
int n,a[200],sum=0;
double avg=0;
//三、数据输入
cin>>n;
for(int i=0;i<n;i++){
cin>>a[i];
sum+=a[i];
}
//四、数据计算
avg=sum*1.0/n;
for(int i=0;i<n-1;i++){
for(int j=0;j<n-i-1;j++){
int temp;
if(a[j]<a[j+1]){
temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
}
//五、输出结果
cout<<sum<<endl;
printf("%.2f\n",avg);
for(int i=0;i<n;i++){
cout<<a[i]<<" ";
}
return 0;
}
问题四:1233 - 求中位数
中位数指的是一组数,如果按照大小排序排好后最中间的那个数的值,如果有偶数个元素,那么就是最中间两个数的平均数!
比如:2 5 8 1 6 ,排序后的结果为 1 2 5 6 8 ,那么这组数的中位数就是 5 !
再比如: 8 9 1 2 3 0 ,排序后的结果为0 1 2 3 8 9 ,那么这组数的中位数就是 (2+3)/2=2.5 。

1.分析问题
- 已知:一组数
- 未知:中位数 median
- 关系:最中间的那个数的值,有偶数个元素,那么就是最中间两个数的平均数
2.定义变量
根据分析的已知,未知按需要定义变量。
//二、数据定义
int n,a[100];
double median;
3.输入数据
从键盘读入。
//三、数据输入
cin>>n;
for(int i=0;i<n;i++){
cin>>a[i];
}
4.数据计算
想要求出一堆数中的中位数,必然先对它们进行排序。
冒泡排序。
//四、数据计算
for(int i=0;i<n-1;i++){
for(int j=0;j<n-i-1;j++){
int temp;
if(a[j]>a[j+1]){
temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
}
if(n%2==0){
median=(a[n/2]+a[n/2-1])*1.0/2;
}else{
median=a[n/2]*1.0;
}
5.输出结果
#include<iostream>
using namespace std;
int main(){
//一、分析问题
//已知:一组数
//未知:中位数 median
//关系:最中间的那个数的值,有偶数个元素,那么就是最中间两个数的平均数
//二、数据定义
int n,a[100];
double median;
//三、数据输入
cin>>n;
for(int i=0;i<n;i++){
cin>>a[i];
}
//四、数据计算
for(int i=0;i<n-1;i++){
for(int j=0;j<n-i-1;j++){
int temp;
if(a[j]>a[j+1]){
temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
}
if(n%2==0){
median=(a[n/2]+a[n/2-1])*1.0/2;
}else{
median=a[n/2]*1.0;
}
//五、输出结果
printf("%.1f",median);
return 0;
}
四、练习
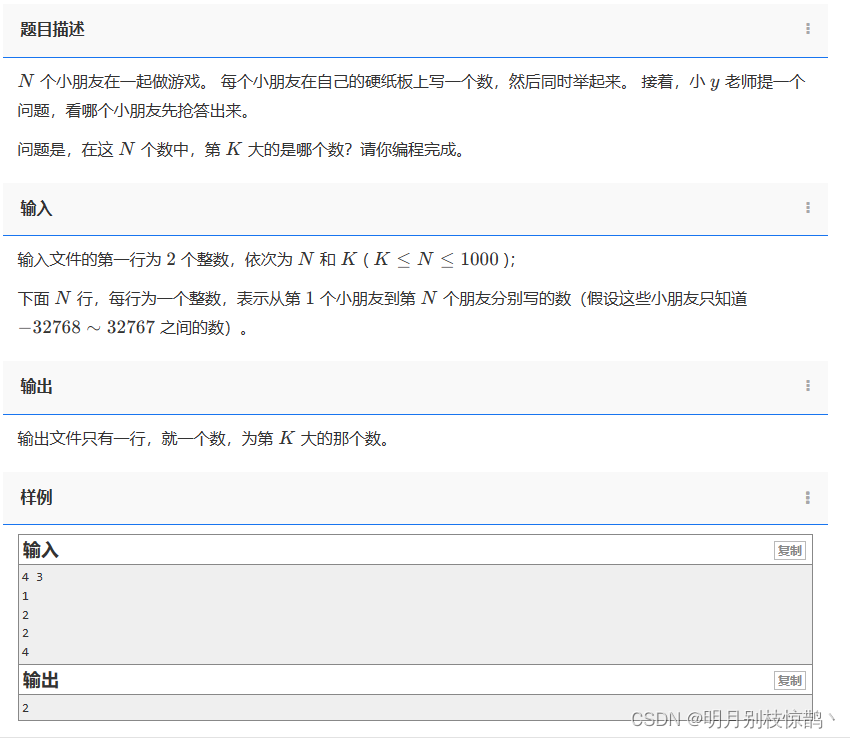
问题一:1172 - 寻找第K大数
问题二:1221 - 优秀成绩的平均分
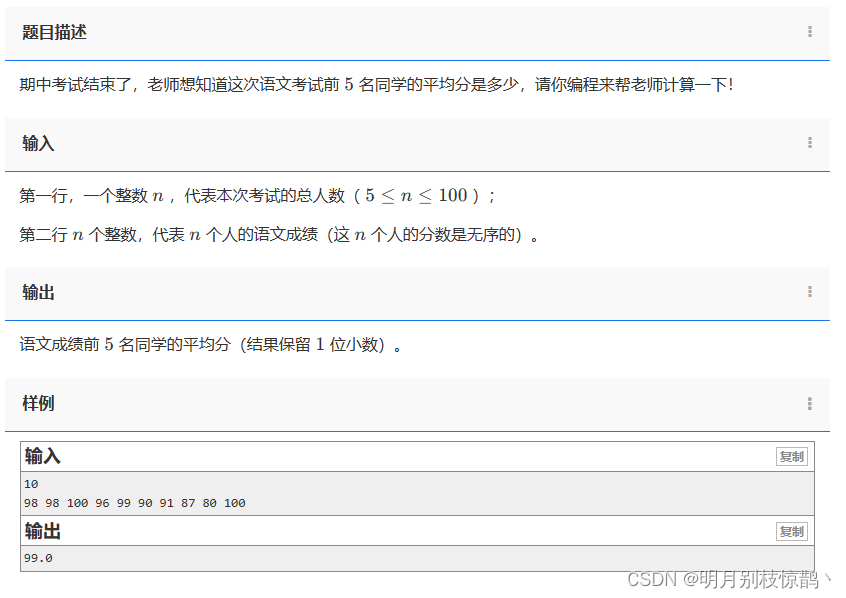
问题三:1242 - 第K大与第K小数
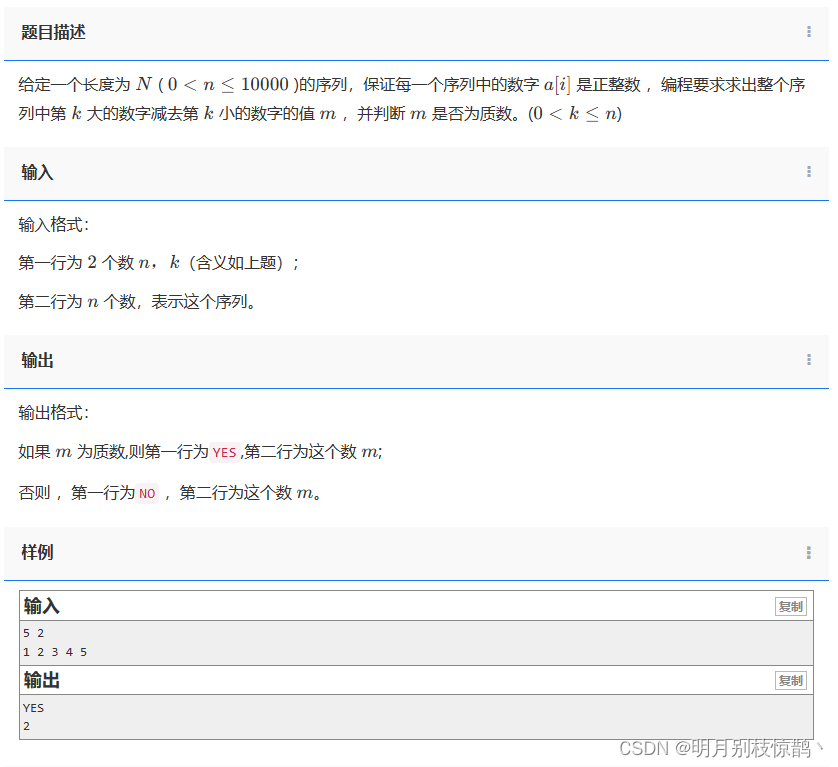
问题四:1399 - 学员的名次?
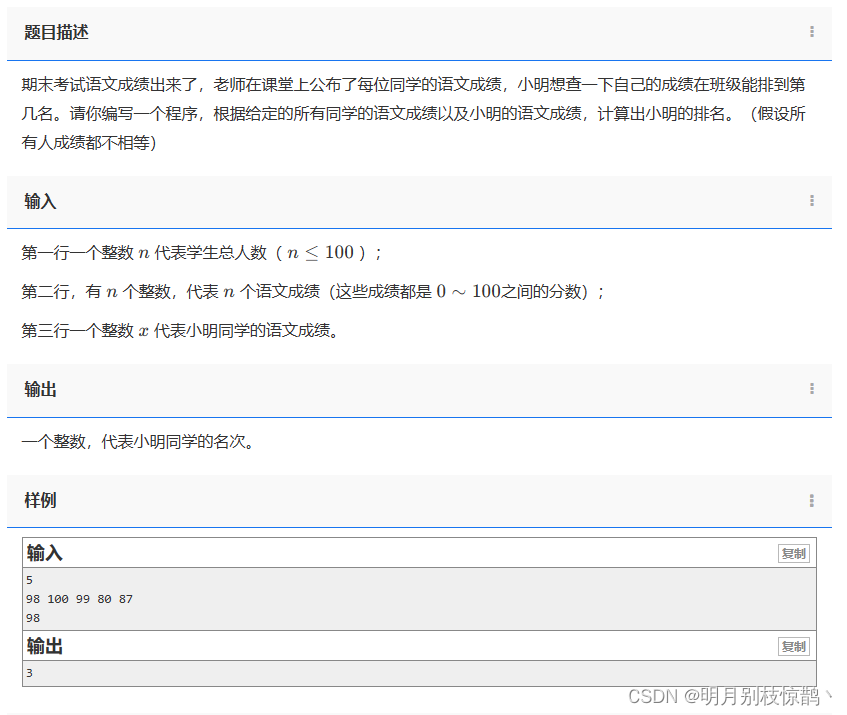
五、总结
以上就是本节关于冒泡排序的全部内容,关于冒泡排序的优化将会在后续补充。
觉得本文还阔以滴,还请点赞、关注、收藏。

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!