加工零件的题解
原题描述:
时间限制: 1000ms
空间限制: 524288kB
题目描述
凯凯的工厂正在有条不紊地生产一种神奇的零件,神奇的零件的生产过程自然也很神奇。工厂里有??位工人,工人们从
编号。某些工人之间存在双向的零件传送带。保证每两名工人之间最多只存在一条传送带。
如果??号工人想生产一个被加工到第
?
阶段的零件,则所有与
号工人有传送带直接相连的工人,都需要生产一个被加工到第?
阶段的零件(但
?号工人自己无需生产第
?阶段的零件)。
如果??号工人想生产一个被加工到第 1 阶段的零件,则所有与?
?号工人有传送带直接相连的工人,都需要为
?号工人提供一个原材料。
轩轩是 1 号工人。现在给出?张工单,第?
张工单表示编号为
??的工人想生产一个第?
阶段的零件。轩轩想知道对于每张工单,他是否需要给别人提供原材料。他知道聪明的你一定可以帮他计算出来!
输入格式
第一行三个正整数,分别表示工人的数目、传送带的数目和工单的数目。
接下来??行,每行两个正整数?
?和?
,表示编号为??
??和
?的工人之间存在一条零件传输带。保证
。
接下来?行,每行两个正整数?
?和?
,表示编号为
?的工人想生产一个第
阶段的零件。
输出格式
共??行,每行一个字符串?
Yes?或者?No。如果按照第张工单生产,需要编号为 1 的轩轩提供原材料,则在第
?行输出?
Yes;否则在第?行输出?
No。注意输出不含引号。
样例 #1
样例输入 #1
3 2 6
1 2
2 3
1 1
2 1
3 1
1 2
2 2
3 2样例输出 #1
No
Yes
No
Yes
No
Yes样例 #2
样例输入 #2
5 5 5
1 2
2 3
3 4
4 5
1 5
1 1
1 2
1 3
1 4
1 5样例输出 #2
No
Yes
No
Yes
Yes提示
【输入输出样例 1 说明】
编号为 1 的工人想生产第 1 阶段的零件,需要编号为 2 的工人提供原材料。
编号为 2 的工人想生产第 1 阶段的零件,需要编号为 1 和 3 的工人提供原材料。
编号为 3 的工人想生产第 1 阶段的零件,需要编号为 2 的工人提供原材料。
编号为 1 的工人想生产第 2 阶段的零件,需要编号为 2 的工人生产第 1 阶段的零 件,需要编号为 1 和 3 的工人提供原材料。
编号为 2 的工人想生产第 2 阶段的零件,需要编号为 1 和 3 的工人生产第 1 阶段的零件,他/她们都需要编号为 2 的工人提供原材料。
编号为 3 的工人想生产第 2 阶段的零件,需要编号为 2 的工人生产第 1 阶段的零件,需要编号为 1 和 3 的工人提供原材料。
【输入输出样例 2 说明】
编号为 1 的工人想生产第 1 阶段的零件,需要编号为 2 和 5 的工人提供原材料。
编号为 1 的工人想生产第 2 阶段的零件,需要编号为 2 和 5 的工人生产第 1 阶段的零件,需要编号为?的工人提供原材料。
编号为 1 的工人想生产第 3 阶段的零件,需要编号为 2 和 5 的工人生产第 2 阶段的零件,需要编号为的工人生产第 1 阶段的零件,需要编号为
?的工人提供原材料。
编号为 1 的工人想生产第 4 阶段的零件,需要编号为 2 和 5 的工人生产第 3 阶段的零件,需要编号为?的工人生产第 2 阶段的零件,需要编号为?
的工人生产第 1 阶段的零件,需要全部工人提供原材料。
编号为 1 的工人想生产第 5 阶段的零件,需要编号为 2 和 5 的工人生产第 4 阶段的零件,需要编号为??的工人生产第 3 阶段的零件,需要编号为?
?的工人生产第 2 阶段的零件,需要全部工人生产第 1 阶段的零件,需要全部工人提供原材料。
【数据规模与约定】
共 20 个测试点。
。
测试点 1~4,。
测试点 5~8,。
测试点 9~12,。
测试点 13~16,。
测试点 17~20,。
题目大意:
有一张无向图,每次有个节点a要级别为L的部件,则与a直接相连的节点要提供L-1的部件。
当节点a要1级的部件时,那么与a直接相连的节点要提供1个原材料。
问你每次节点1是否提供原材料。
主要思路:
这个题目可以用分类讨论。
分三个部分:(用cnt表示从节点a到1的路径长度(每条边长为1)
- L = cnt
- L<cnt
- L>cnt
对于部分1:
画图来看一下。

当L=cnt时,节点1要提供原材料。
注意:有些童鞋会说:4生产3,那么5又要生产2,不是还要进一步的推导吗?
可是题目中只说是否要1提供原材料,其他的就不用管太多。
第二部分:
L<cnt
还是画图:

我们发现,还没轮到1时,就结束了,说明1不用提供什么。
第三部分:
L>cnt
从x走到1时L是奇数。
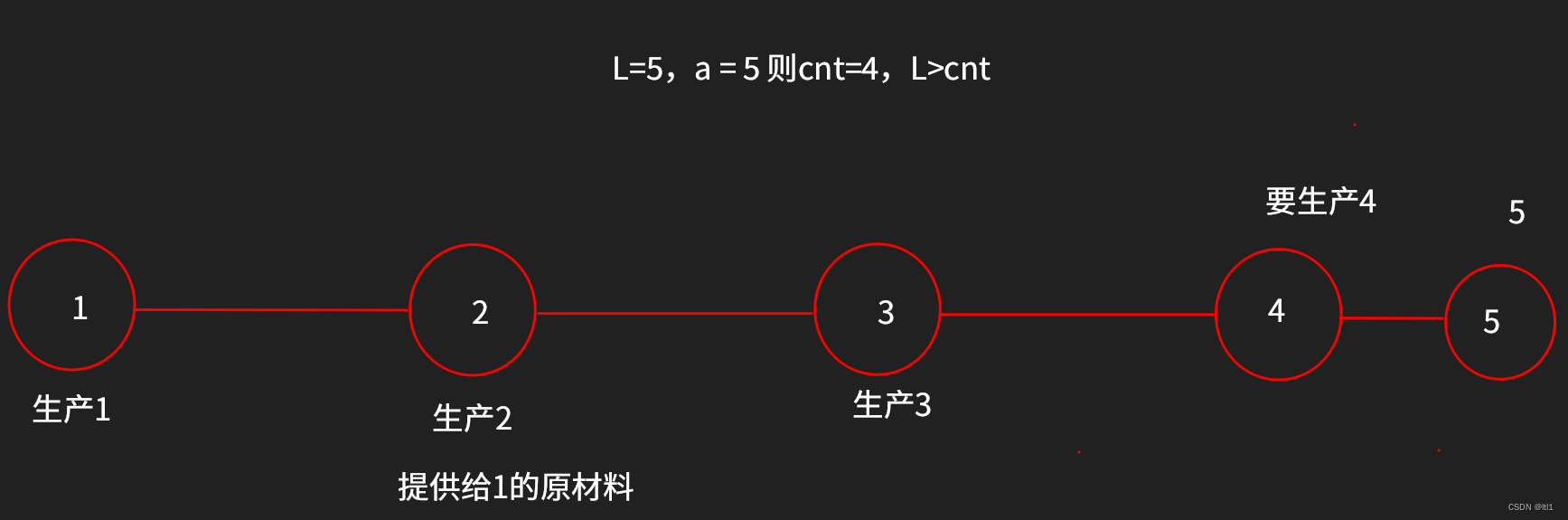
1不用提供任何原材料
但是but,当L>cnt?且从x走到1时L是偶数。
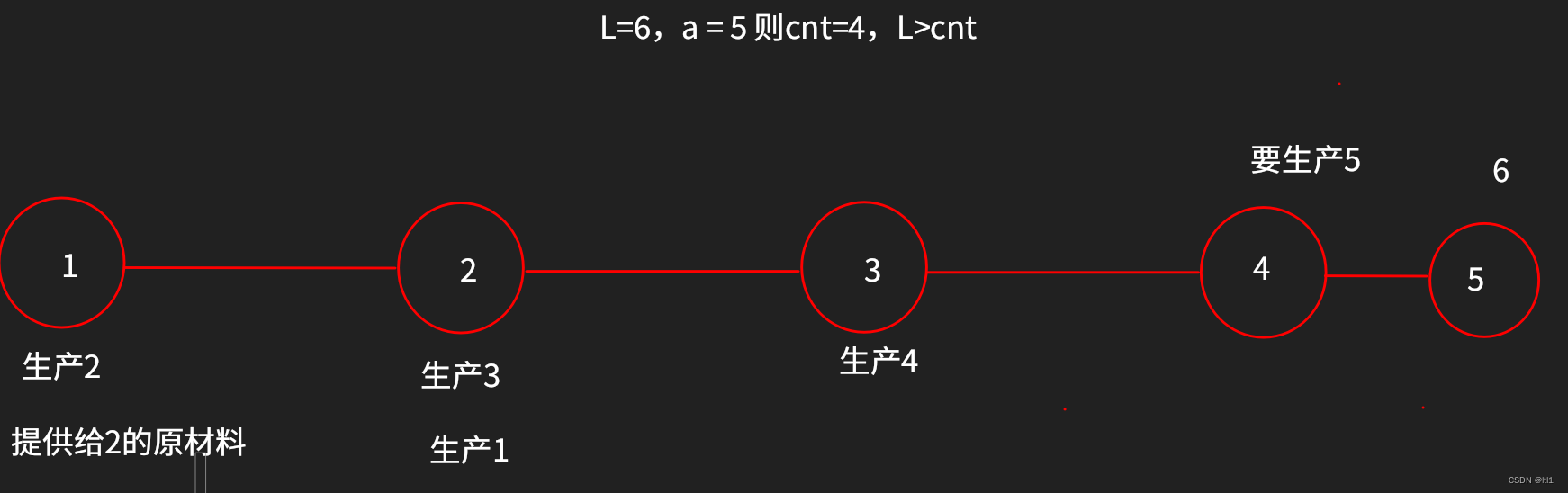
这时,1要提供原材料了。
得出结论:
当L = cnt,1要提供原材料。
当L < cnt,1不用提供任何原材料。
当L > cnt,且从x走到1时L-cnt是奇数,1不用提供任何原材料。
当L > cnt,且从x走到1时L是偶数,1要提供原材料。
但是我们怎么才能判断出x走到1时L是偶数还是奇数呢?
int even[100010];// even[x]表示:从1走到x,长度最短为偶数的路径的长度(even是偶数的意思)
int odd[100010];// odd[x]表示:从1走到x,长度最短为奇数的路径的长度(odd是奇数的意思)注:是最短路径。
奇数-奇数=偶数。
奇数-偶数=奇数
偶数-奇数=奇数
偶数-偶数=偶数。
cnt被替代了
这样我们就发现了:
L是奇数,且l>=odd[x](odd[x]肯定是奇数长度路径)那么就输出"Yes"(等于也输出Yes)
L是奇数,且l<odd[x](odd[x]肯定是奇数长度路径)那么就输出"No"
L是偶数,且l>=even[x](even[x]肯定是偶数长度路径)那么就输出"Yes"(等于也输出Yes)
L是偶数,且l<even[x](even[x]肯定是偶数长度路径)那么就输出"No"
不明白为啥就看重新看一下三个部分。
初始化:
都初始化成0x3f(是一个较大数就可以了)?
代码code:
#include<bits/stdc++.h>
using namespace std;
int n,m,q;
int even[100010];// even[x]表示:从1走到x,长度最短为偶数的路径的长度(even是偶数的意思)
int odd[100010];// odd[x]表示:从1走到x,长度最短为奇数的路径的长度(odd是奇数的意思)
vector<vector<int>> v(100010);
//int vis[100010][10010];
void init()
{
queue<pair<int,int>> q;
q.push({1,0});
while(!q.empty())
{
int node=q.front().first,step=q.front().second;
q.pop();
for(auto it:v[node])
{
if(step%2 == 1&&step+1<even[it])
{
even[it] = step+1;
// vis[it][step+1] = 1;
q.push({it,step+1});
}
if(step%2 == 0&&step+1<odd[it])//这里用了最短路原理
{
odd[it] = step+1;
// vis[it][step+1] = 1;
q.push({it,step+1});
}
/*
有些童鞋会说,这里odd是奇数,可是为啥是放在step%2 == 0,里面不应该是放even吗。
回答:step还要+1,因为已经走了这一步,要加一,偶数加1就是奇数,所以是odd放在里面。
18行~23行同理
*/
}
}
}
int main()
{
cin>>n>>m>>q;
for(int i=1;i<=m;i++)
{
int u,v1;
cin>>u>>v1;
v[u].push_back(v1);
v[v1].push_back(u);
}
memset(odd,0x3f,sizeof(odd));
memset(even,0x3f,sizeof(even));
init();
while(q--)
{
int l,x;
cin>>x>>l;
if(l%2 == 1)
{
if(l>=odd[x])
{
cout<<"Yes\n";
}
else
{
cout<<"No\n";
}
}
else
{
if(l>=even[x])
{
cout<<"Yes\n";
}
else
{
cout<<"No\n";
}
}
}
return 0;
}本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 软件测试面试总结分享
- Docker篇之修改docker默认磁盘占用目录
- 从吉客云到金蝶云星空通过接口配置打通数据
- 华为openEuler使用阿里云yum源
- PDF 文件操作指南
- C语言实现动态数组
- 司铭宇老师:家具导购销售培训:家具导购员销售技巧和话术
- 【论文阅读笔记】4篇Disentangled representation learning用于图像分割的论文
- WXUI 基于uni-app x开发的高性能混合UI库
- R语言——R函数、选项参数、数学统计函数(六)