数据流的中位数

题目链接

数据流的中位数

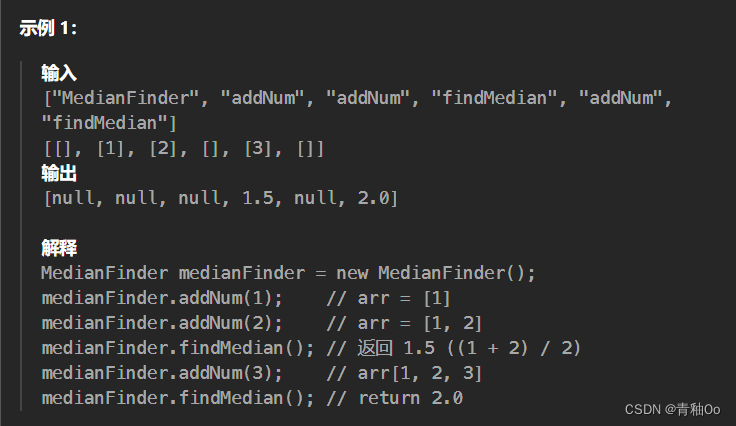
题目描述

注意点

• 在调用 findMedian 之前，数据结构中至少有一个元素
• 如果列表的大小是偶数，则没有中间值，中位数是两个中间值的平均值

解答思路

• 使用两个优先队列存储数据流，其中一个优先队列队首为最大元素，另一个队首为最小元素，始终保持两个优先队列元素数量平衡，计算中位数只需要取优先队列的队首即可，不需要对其他元素进行排序

代码

class MedianFinder {
    // 队首为最小元素
    PriorityQueue<Integer> minQueue;
    // 队首为最大元素
    PriorityQueue<Integer> maxQueue;

    public MedianFinder() {
        minQueue = new PriorityQueue<>((a, b) -> (b - a));
        maxQueue = new PriorityQueue<>((a, b) -> (a - b));
    }
    
    public void addNum(int num) {
        if (minQueue.isEmpty()) {
            minQueue.offer(num);
            return;
        }
        if (num < minQueue.peek()) {
            minQueue.offer(num);
            if (minQueue.size() > maxQueue.size() + 1) {
                maxQueue.offer(minQueue.poll());
            }
        } else {
            maxQueue.offer(num);
            if (maxQueue.size() > minQueue.size()) {
                minQueue.offer(maxQueue.poll());
            }
        }
    }
    
    public double findMedian() {
        if ((minQueue.size() + maxQueue.size()) % 2 == 0) {
            return (double) (minQueue.peek() + maxQueue.peek()) / 2;
        } else {
            return minQueue.peek();
        }
    }
}

关键点

• 优先队列加入数字时始终保持队首为最大或最小数字
• 始终保持两个优先队列的容量大小不超过1，在计算中位数时只需要取队首的元素即可