【代码随想录】刷题笔记Day48
发布时间:2024年01月09日
前言
- 早上练车去了(好久没有8点前醒了),练科目二两小时下来脚根可真酸啊,希望下周一把过。练完顺带去Apple西湖免费换新了耳机,羊毛爽!
121. 买卖股票的最佳时机 - 力扣(LeetCode)
-
贪心法
- 更新最小值,更新最大区间利润值
-
class Solution { public: int maxProfit(vector<int>& prices) { int low = INT_MAX; int result = 0; for (int i = 0; i < prices.size(); i++) { low = min(low, prices[i]); // 取最左最小价格 result = max(result, prices[i] - low); // 直接取最大区间利润 } return result; } };
-
动规法(一维)
- 一维思路和贪心类似,有点难理解
- dp[i]含义
- 以prices[i]价格卖出可获得的最大利润
- ?递推公式
- 情况一:i-1买入,i卖出,收益prices[i] - prices[i-1]
- 情况二:i-1之前已卖出,如果延迟到i卖出,取更高的收益
- dp[i]?= max(prices[i] - prices[i-1], prices[i] - prices[i-1] + dp[i-1]);
- 初始化及顺序
- dp[0] = 0,从前往后
- 要最高收益,结果取dp[i]的最大值(和其他一维有差别),另外可以优化一下空间
-
// 优化前 class Solution { public: int maxProfit(vector<int>& prices) { int len = prices.size(); vector<int> dp(len); int result = 0; for(int i = 1; i < len; i++){ dp[i] = max(prices[i] - prices[i - 1], prices[i] - prices[i - 1] + dp[i - 1]); result = max(result, dp[i]); } return result; } }; // 优化后 class Solution { public: int maxProfit(vector<int>& prices) { int len = prices.size(); int dp0 = 0, dp1 = 0; // 只需要维护滚动两个值 int result = 0; for(int i = 1; i < len; i++){ dp1 = max(prices[i] - prices[i - 1], prices[i] - prices[i - 1] + dp0); result = max(result, dp1); dp0 = dp1; // 互换 } return result; } };
-
动规法(二维)
- 二维用的01双状态,类似打家劫舍III
- dp数组含义
- dp[i][0] 表示第i天持有股票所得最多现金:维持现状 + 买入股票
- dp[i][1] 表示第i天不持有股票所得最多现金:维持现状 + 卖出股票
- 递推公式
- dp[i][0] = max(dp[i - 1][0], -prices[i]);
- dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);
- 初始化及顺序
- dp[0][0] = -prices[0];? dp[0][1] = 0;? 从前往后
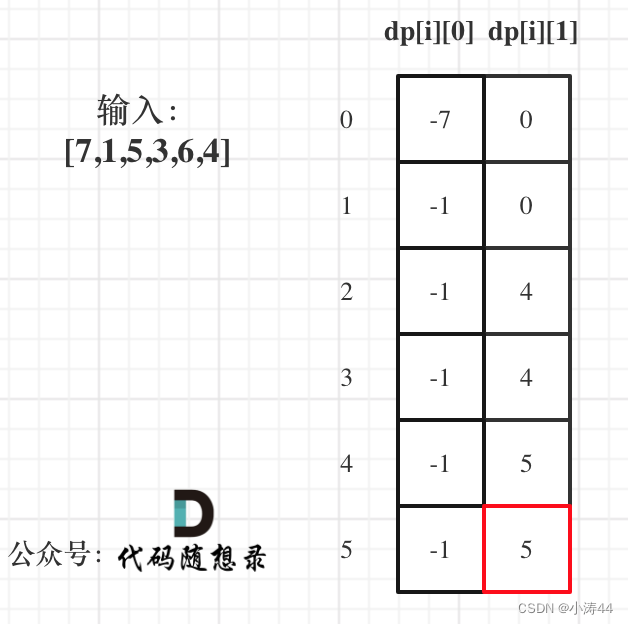
- 答案取dp[max][1],因为不持有一定比持有多
-
class Solution { public: int maxProfit(vector<int>& prices) { int len = prices.size(); vector<vector<int>> dp(len, vector<int>(2)); dp[0][0] -= prices[0]; for(int i = 1; i < len; i++){ // 持有:原状 + 买入 dp[i][0] = max(dp[i - 1][0], -prices[i]); // 不持有:原状 + 卖出持有 dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]); } return dp[len - 1][1]; } };
后言
-
先到这(饿了),看评论区尝试了一下一维和改进废了些时间,晚上有空继续刷股票
文章来源:https://blog.csdn.net/qq_56077562/article/details/135481431
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章