【上分日记】第381场周赛(差分 + 分类讨论)

前言

?这次博主做了三道题，算是第一次，看来是题出的简单了（hhh，小白勿喷），不过还是有不错的进步，继续加油，这次最后一题分类讨论也是挺让人头疼的，下面我们好好总结一下。

正文

1.3017. 按距离统计房屋对数目 II

• 题目链接：3017. 按距离统计房屋对数目 II

---

• 题目思路：

?这道题算是折磨了我一整天，虽然分类讨论出来了，但是实现代码时细节比较多，一不小心出现一个失误就要debug好久。

下面我们来仔细分析一下：

• 前置知识：1094. 拼车——差分模版题，看灵神题解快速掌握。

1. 我们先从大体上分析一下：

• 我们可以先统计出不看 x,y 联系的最短距离，再根据 x,y 对一个点的影响再进行分类讨论，从而得出最短距离。
• 而且所有房屋的编号是按顺序的，房子的最大编号为n，那么设 i 号房屋，不看x , y 产生的距离可对i左边分析距离在[1, i - 1]之间， 再对i右边分析距离在[1, n - i ]之间，那么这些距离都产生了一次.
• 那么我们就可以联系到差分数组，对这些距离出现的次数可以在O(1)的时间复杂度加1，也就是说我们可以用一个存放距离出现次数的差分数组，快速统计距离出现次数。
• 最后我们再讨论x , y 带来的影响，对产生影响的区间撤销再补充即可。

2. 其次我们再对 x, y 产生的影响，根据房子的编号进行分类讨论。以下得保证 x <= y。

1. 当x + 1 >= y 时, x y 联系起来没有影响。
2. 当x + 1 > y 时，x y 联系起来对房子编号产生的最短距离有影响，设房子编号为i。

1. i <= x时:

• 对于i 到 [y, n]的距离范围 [y - i, n - i] 产生了影响，进行撤销，缩短的距离为dec = y - x - 1, 这里的1是 y 到 x的一步距离，因此缩短之后的距离范围为[y - i - dec, n - i - dec]。
• 对于i 到 (x,y)的距离，我们可以设其中一点为 j，设 j - i > (x - i + 1) + (y - j) 得出 j > (x+y+1) / 2, 因此可以得出j的准确范围为[(x + y + 1) / 2 + 1, y - 1], 那么可以得到原来的距离范围d_pre准确为 [ (x + y + 1) / 2 + 1 - i, y - 1 - i], 对其进行撤除，且可以得到现在的距离范围d_current准确的是[x - i + 2, (x - i + 1) + y - ((x + y + 1) / 2 + 1)]，化简成 [x - i + 2, (x+ y) - (x + y + 1) / 2 - i] 即可，再化简就出bug(是上下取整的问题)了。

2. x < i < ( x + y ) / 2 时，x 与 y 相连对中间的点(x + y) / 2 无影响。

• 对于[y , n] 点产生的距离 [y - i, n - i] 产生了影响，进行撤销，缩短的距离为dec = (y-i)- (i-x+1),整理得dec = y + x - 1 - 2 * i, 则添加的距离为[y - i - dec, n - i - dec].
• 对于[x, y ] 点产生影响的范围我们可以设其中一点为j, 设 j - i > (i - x + 1) + (y - j) 得出的j的表达式结果为：j > i + (y - x + 1) / 2, 得出 j 准确范围为[i + (y - x + 1) / 2 + 1, y - 1], 可以得出对[x,y]产生影响的原先的距离为d_prev [(y - x + 1) / 2 + 1, y - 1 - i], 且产生影响的现在的距离范围准确为[i - x + 2, i - x + 1 + y - (i + (y - x + 1) / 2 + 1)], 化简得[i - x + 2, y - x - (y - x + 1) / 2]，无需再进一步化简，同理。

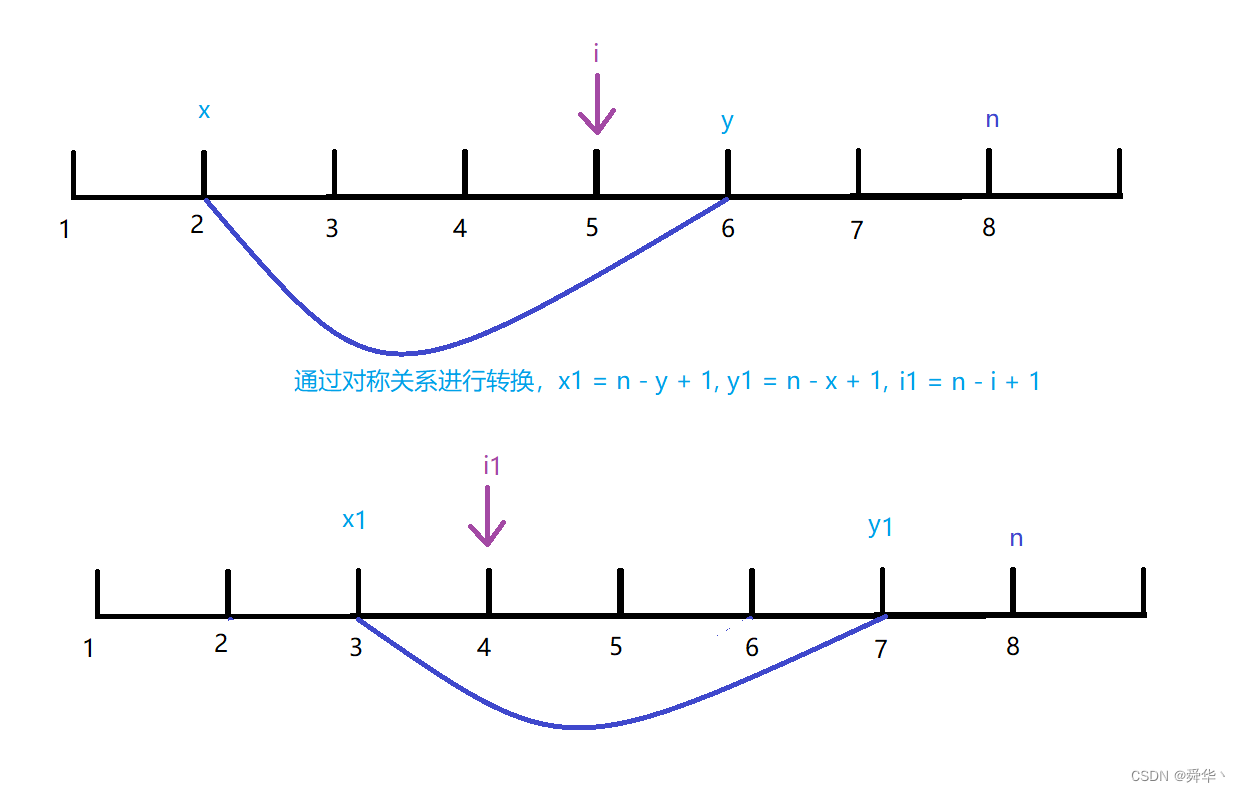
3. (x + y + 1) / 2 < i < y时，如果 x + y 为奇数，(x + y + 1) / 2 是 偏右边的中间点，如果 x + y 为偶数，那么其为中间点。左边的

• 可通过下图对称转换为第2种情况，

4. i >= y 时，也可通过上图的进行转换，从而转换为第1种情况。

• 实现代码：

class Solution {
public:
    vector<long long> countOfPairs(int n, int x, int y) 
    {
        if(x > y) swap(x,y);
        vector<int> dif(n + 1,0);
        auto add = [&](int left,int right)
        {
            if(left > right) return;

            dif[left]++;
            dif[right + 1]--;
        };
        auto sub = [&](int left,int right)
        {
            if(left > right) return;
            dif[left]--;
            dif[right + 1]++;
        };
        auto update1 = [&](int x,int y,int i)
        {
            int dec = y - x - 1;
            //对[y - i,n - i]进行撤销
            //再对[y - i - dec,n - i - dec]添加
            sub(y-i,n-i);
            add(y-i-dec,n-i-dec);
            //再对[(x + y + 1) / 2 + 1 - i,y-1-i]撤销
            sub((x + y + 1)/2 + 1 - i, y - 1 - i);
            //再对[x-i+2,(x+y-1) / 2 - i] 添加
            add(x - i + 2, (y - x) / 2 - i);
        };
        auto update2 = [&](int x,int y, int i)
        {
            int dec = x + y - 1 - 2 * i;
            //对[y - i,n - i]进行撤销
            sub(y-i,n-i);
            //对[y - i - dec,n - i - dec]进行添加
            add(y - i - dec, n -i - dec);

            //对[(y - x + 1) / 2 + 1 - i, y - 1 - i]进行撤销
            sub((y - x + 1) / 2 + 1, y - 1 - i);
            //对[i - x + 2,  (y - x - 1) / 2]进行添加
            add(i - x + 2, y - x - (y - x + 1) / 2);
        };
        for(int i = 1; i <= n; i++)
        {
            add(1,i-1);add(1,n-i);
            if(x + 1 >= y) continue;
            else if(i <= x)
                update1(x,y,i);
            else if(i >= y)
                update1(n - y + 1, n - x + 1, n - i + 1);
            else if(i > (x + y + 1) / 2)
                update2(n - y + 1, n - x  + 1, n - i + 1);
            else if(i < (x + y) / 2)
                update2(x,y,i);
        }
        //差分相加得距离的次数。
        vector<long long> ans(n);
        long long sum = 0;
        for(int i = 1; i <= n; i++)
        {
            sum += dif[i];
            ans[i-1] = sum;
        }
        return ans;
    }
};  

总结

?本次周赛学到了差分，对分类讨论有了更为深刻的理解，看来有良好的数学功底，对于解这种题帮助还是很大的。

尾序

?我是舜华，期待与你的下一次相遇！