Grind75第10天 | 133.克隆图、994.腐烂的橘子、79.单词搜索

133.克隆图

题目链接：https://leetcode.com/problems/clone-graph

解法：

这个题是对无向图的遍历，可以用深度优先搜索和广度有限搜索。

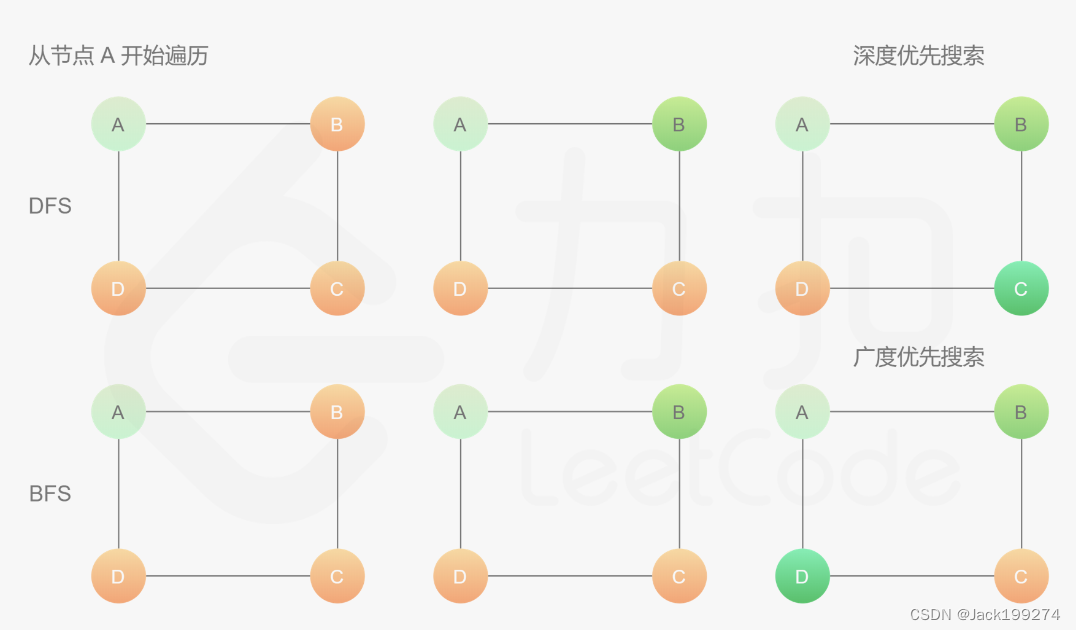
下面这个图比较清楚的说明了两种方法的区别。

DFS：从A开始克隆，遍历两个邻居B和D，遍历到B时，不管D了，继续遍历B的邻居A和C。其中A遍历过了，跳过。

BFS：从A开始克隆，遍历两个邻居B和D，B和D都遍历完了，再遍历B的邻居A和C。其中A遍历过了，跳过。

需要设置一个哈希表，记录遍历过的节点和它的克隆节点，以便再次遇到时直接返回，不需要再克隆。

参考题解：DFS+BFS

边界条件：

时间复杂度：O(N)，其中?N?表示节点数量

空间复杂度：O(N)。存储克隆节点和原节点的哈希表需要?O(N)的空间

"""
# Definition for a Node.
class Node:
    def __init__(self, val = 0, neighbors = None):
        self.val = val
        self.neighbors = neighbors if neighbors is not None else []
"""
# DFS
from typing import Optional
class Solution:
    def cloneGraph(self, node: Optional['Node']) -> Optional['Node']:
        self.visited = {}
        return self.dfs(node)

    def dfs(self, node):
        if not node:
            return None
        # 已经访问过，则直接返回克隆节点
        if node in self.visited:
            return self.visited[node]
        # 创建克隆节点
        clone_node = Node(node.val, [])
        # 标记为已访问
        self.visited[node] = clone_node

        # 遍历该节点的邻居，并递归的克隆邻居
        if node.neighbors:
            clone_node.neighbors = [self.dfs(n) for n in node.neighbors]
        return clone_node

"""
# Definition for a Node.
class Node:
    def __init__(self, val = 0, neighbors = None):
        self.val = val
        self.neighbors = neighbors if neighbors is not None else []
"""
# BFS
from typing import Optional
class Solution:
    def cloneGraph(self, node: Optional['Node']) -> Optional['Node']:
        if not node:
            return None

        visited = {}
        que = deque([node])
        visited[node] = Node(node.val, [])
        while que:
            cur_node = que.popleft()
            # 遍历邻居
            for n in cur_node.neighbors:
                if n not in visited:
                    # 如果邻居没有被访问，则没有被克隆，那么克隆
                    visited[n] = Node(n.val, [])
                    # 并把邻居加入队列
                    que.append(n)
                # 更新克隆节点的邻居
                visited[cur_node].neighbors.append(visited[n]) 
        return visited[node]

994.腐烂的橘子

题目链接：https://leetcode.com/problems/rotting-oranges

解法：

这个题和【542.01矩阵】有点像，都是先把某个特定值的点加入到队列中，作为第0层，然后进行广度优先搜索，遍历第1层，第2层...

从某个结点出发，BFS 首先遍历到距离为 1 的结点，然后是距离为 2、3、4…… 的结点。因此，BFS 可以用来求最短路径问题。

题目要求：返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。翻译一下，实际上就是求腐烂橘子到所有新鲜橘子的最短路径。

我们首先找出所有腐烂的橘子，将它们放入队列，作为第 0 层的结点。

然后进行 BFS 遍历，对上、下、左、右四个方向的结点进行污染，同时加入队列，作为第1层的节点。此时过去了一分钟。下一次BFS，需要一次性遍历第1层的所有节点，并且时间再加1分钟。

由于可能存在无法被污染的橘子，我们需要提前记录新鲜橘子的数量。在 BFS 中，每遍历到一个橘子（污染了一个橘子），就将新鲜橘子的数量减一。

BFS 结束后，新鲜橘子的数量仍未减为零，说明存在无法被污染的橘子，返回为-1，否则分钟数。

参考题解：BFS

边界条件：无

时间复杂度：O(mn)

空间复杂度：O(mn)

class Solution:
    def orangesRotting(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        que = deque()

        # 统计新鲜橘子的个数，并把腐烂橘子加入到队列
        count = 0
        for r in range(m):
            for c in range(n):
                if grid[r][c] == 1:
                    count += 1
                elif grid[r][c] == 2:
                    que.append((r,c))

        # 记录分钟数
        minute = 0
        directions = [(-1,0), (1,0), (0,-1), (0,1)]
        while count > 0 and que:
            minute += 1
            # 注意这里不要命名为n，因为上面已经令n=len(grid[0])
            size = len(que)
            # 注意这里有循环，要把这一层一次性遍历完，因为这样1分钟内这一层都会腐烂
            for i in range(size):
                r, c = que.popleft()
                for d in directions:
                    n_r, n_c = r+d[0], c+d[1]
                    if 0 <= n_r < m and 0 <= n_c < n and grid[n_r][n_c] == 1:
                        grid[n_r][n_c] = 2
                        que.append((n_r, n_c))
                        count -= 1
        if count > 0:
            return -1
        return minute

79.单词搜索

题目链接：https://leetcode.com/problems/word-search

解法：

这个题用回溯，回溯本身也是一种深度优先搜索。

从网格的每一个位置?(i,j) 出发，从上下左右4个方位去搜索k步（k为word的长度），搜到则返回True，否则从另一个位置出发去搜索。

减枝操作就是如果访问过了，就直接返回。

这个题没啥好说的，直接参考题解：深度优先搜索+回溯

边界条件：无

k 为 wod 的长度。

class Solution:
    def exist(self, board: List[List[str]], word: str) -> bool:
        self.word = word

        for i in range(len(board)):
            for j in range(len(board[0])):
                if self.dfs(board, i, j, 0): return True
        return False
    
    def dfs(self, board, i, j, k):
        # 如果越界
        if i < 0 or i >= len(board) or j < 0 or j >= len(board[0]):
            return False
        # 如果不相等
        if board[i][j] != self.word[k]:
            return False
        # 如果匹配完毕
        if k == len(self.word) - 1:
            return True
        
        board[i][j] = ''
        directions = [(-1, 0), (1,0), (0,-1), (0,1)]
        for d in directions:
            if self.dfs(board, i+d[0], j+d[1], k+1):
                return True
        board[i][j] = self.word[k]
        return False