吴恩达深度学习l2week1编程作业—Regularization(中文跑通版)
1.Packages
# import packages
import numpy as np
import matplotlib.pyplot as plt
import sklearn
import sklearn.datasets
import scipy.io
from reg_utils import sigmoid, relu, plot_decision_boundary, initialize_parameters, load_2D_dataset, predict_dec
from reg_utils import compute_cost, predict, forward_propagation, backward_propagation, update_parameters
from testCases import *
from public_tests import *
%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
%load_ext autoreload
%autoreload 22.Problem Statement
你刚刚被法国足球公司聘为人工智能专家。他们希望你推荐法国队守门员踢球的位置,这样法国队的球员就可以用头击球。

3.加载数据集
train_X, train_Y, test_X, test_Y = load_2D_dataset()
每个点对应于足球场上的一个位置,在法国守门员从足球场左侧射门后,足球运动员用他的/她的头击球。
如果这个点是蓝色的,那就意味着法国球员成功地用头击球了
如果圆点是红色的,则表示对方球员用头击球
你的目标:使用深度学习模型来找到守门员应该踢球的位置。
数据集分析:这个数据集有点嘈杂,但看起来像是将左上半部分(蓝色)和右下半部分(红色)分隔开的对角线会很好。
您将首先尝试一个非正则化模型。然后你将学习如何规范它,并决定你将选择哪种模式来解决法国足球公司的问题。
4.非正则化模型
您将使用以下神经网络(已在下面为您实现)。此模型可用于:
在正则化模式下——通过将lambd输入设置为非零值。我们使用“lambd”而不是“lambda”,因为“lambda”是Python中的保留关键字。
在dropout模式里,将keep_prob设置为小于1的值
首先尝试不使用任何正则化模型,然后实现:
L2 regularization:函数--"compute_cost_with_regularization()" and "backward_propagation_with_regularization()"
Dropout:函数--?"forward_propagation_with_dropout()" and "backward_propagation_with_dropout()"
在每一部分中,您都将使用正确的输入运行此模型,以便它调用您已实现的函数。看一下下面的代码,以熟悉该模型。
def model(X, Y, learning_rate = 0.3, num_iterations = 30000, print_cost = True, lambd = 0, keep_prob = 1):
grads = {}
costs = [] # to keep track of the cost
m = X.shape[1] # number of examples
layers_dims = [X.shape[0], 20, 3, 1]
# Initialize parameters dictionary.
parameters = initialize_parameters(layers_dims)
# Loop (gradient descent)
for i in range(0, num_iterations):
# Forward propagation: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID.
if keep_prob == 1:
a3, cache = forward_propagation(X, parameters)
elif keep_prob < 1:
a3, cache = forward_propagation_with_dropout(X, parameters, keep_prob)
# Cost function
if lambd == 0:
cost = compute_cost(a3, Y)
else:
cost = compute_cost_with_regularization(a3, Y, parameters, lambd)
# Backward propagation.
assert (lambd == 0 or keep_prob == 1) # it is possible to use both L2 regularization and dropout,
# but this assignment will only explore one at a time
if lambd == 0 and keep_prob == 1:
grads = backward_propagation(X, Y, cache)
elif lambd != 0:
grads = backward_propagation_with_regularization(X, Y, cache, lambd)
elif keep_prob < 1:
grads = backward_propagation_with_dropout(X, Y, cache, keep_prob)
# Update parameters.
parameters = update_parameters(parameters, grads, learning_rate)
# Print the loss every 10000 iterations
if print_cost and i % 10000 == 0:
print("Cost after iteration {}: {}".format(i, cost))
if print_cost and i % 1000 == 0:
costs.append(cost)
# plot the cost
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (x1,000)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters接下来不用任何正则化训练模型,来看看训练/测试集的精确度
parameters = model(train_X, train_Y)
print ("On the training set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)
训练准确率为94.8%,测试准确率为91.5%。这是基线模型(下面,您将观察正则化对该模型的影响)。运行以下代码来绘制模型的决策边界。
plt.title("Model without regularization")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
非正则化模型显然与训练集过拟合。它适合嘈杂的点!现在让我们来看两种减少过拟合的技术。
5.L2 Regularization
避免过拟合的标准方法称为L2正则化。它包括适当地修改您的成本函数,从:

Exercise 1 - compute_cost_with_regularization

def compute_cost_with_regularization(A3, Y, parameters, lambd):
"""
用L2正则化实现代价函数。见上述公式(2)。
A3——激活后,正向传播的输出,形状(输出大小,示例数)
Y——“真”标签矢量,形状(输出大小,示例数)
parameters——包含模型参数的python字典
正则化损失函数的代价值(公式(2))
"""
m = Y.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
W3 = parameters["W3"]
cross_entropy_cost = compute_cost(A3, Y) # 交叉熵的部分
L2_regularization_cost = (1/m)*(lambd/2)*(np.sum(np.square(W1))+np.sum(np.square(W2))+np.sum(np.square(W3)))
cost = cross_entropy_cost + L2_regularization_cost
return costA3, t_Y, parameters = compute_cost_with_regularization_test_case()
cost = compute_cost_with_regularization(A3, t_Y, parameters, lambd=0.1)
print("cost = " + str(cost))
compute_cost_with_regularization_test(compute_cost_with_regularization)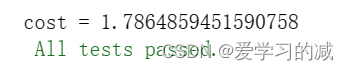
Exercise 2 - backward_propagation_with_regularization

def backward_propagation_with_regularization(X, Y, cache, lambd):
"""
实现我们的基线模型的向后传播,我们在其中添加了L2正则化。
X——输入数据集,形状(输入大小,示例数)
Y——“真”标签矢量,形状(输出大小,示例数)
cache—缓存forward_propation()的输出
lambd——正则化超参数,标量
梯度——关于每个参数、激活和预激活变量的梯度字典
"""
m = X.shape[1]
(Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1./m * np.dot(dZ3, A2.T) + (lambd/m)* W3
db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True)
dA2 = np.dot(W3.T, dZ3)
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1./m * np.dot(dZ2, A1.T) + (lambd/m)* W2
db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True)
dA1 = np.dot(W2.T, dZ2)
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1./m * np.dot(dZ1, X.T) + (lambd/m)* W1
db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradientst_X, t_Y, cache = backward_propagation_with_regularization_test_case()
grads = backward_propagation_with_regularization(t_X, t_Y, cache, lambd = 0.7)
print ("dW1 = \n"+ str(grads["dW1"]))
print ("dW2 = \n"+ str(grads["dW2"]))
print ("dW3 = \n"+ str(grads["dW3"]))
backward_propagation_with_regularization_test(backward_propagation_with_regularization)

parameters = model(train_X, train_Y, lambd = 0.7)
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)值得庆幸的是,测试集的准确率提高到93%。你拯救了法国足球队!
您不再过度拟合训练数据。让我们画出决策边界。
plt.title("Model with L2-regularization")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
观察结果:
𝜆是一个超参数,您可以使用开发集进行调整。L2正则化使您的决策边界更平滑。如果𝜆太大,也有可能“过平滑”,导致模型具有高偏差high bias。
L2正则化实际上在做什么?:
L2正则化依赖于具有小权重的模型比具有大权重的模型更简单的假设。因此,通过惩罚成本函数中权重的平方值,您可以将所有权重降到更小的值。权重太大,成本太高了!这导致了一个更平滑的模型,其中输出随着输入的变化而变化得更慢。
你应该记住的是:L2正则化对以下方面的影响:
成本计算:将正则化项添加到成本中。
反向传播功能:在相对于权重矩阵的梯度中存在额外的项。
weights权重最终会变小(“weight decay”):权重被推到较小的值。
6.Dropout
最后,dropout是一种广泛使用的正则化技术,专门用于深度学习。它在每次迭代iteration中随机关闭一些神经元。看这两个视频,看看这意味着什么!

在每次迭代中,你关闭(=设置为零)一层的每个神经元,概率为1/𝑘𝑒𝑒𝑝_𝑝𝑟𝑜𝑏或者保持概率𝑘𝑒𝑒𝑝_𝑝𝑟𝑜𝑏(此处为50%)。丢弃的神经元没有作用到迭代的前向和后向传播的训练。

第一层:我们关闭了平均40%的神经元;第三层:我们关闭了平均20%的神经元
当你关闭一些神经元时,你实际上修改了你的模型。退出背后的想法是,在每次迭代中,你训练一个只使用神经元子集的不同模型。随着脱落,你的神经元对另一个特定神经元的激活变得不那么敏感,因为另一个神经元可能随时关闭。
6.1 带Dropout的前向传播
Exercise 3 - forward_propagation_with_dropout
实现带Dropout的正向传播。您使用的是一个3层神经网络,并将Dropout添加到第一和第二隐藏层。我们不会将dropout应用于输入层或输出层。

def forward_propagation_with_dropout(X, parameters, keep_prob = 0.5):
"""
实现前向传播:LINERAL->RELU+DROPOUT->LINERAL->RELU+DROPOUT->LINERAR->SIGMOID。
X——输入数据集,形状(2,示例数)
parameters--包含参数“W1”、“b1”、“W2”、“b2”、“W3”、”b3“的python字典:
W1——形状的权重矩阵(20,2)
b1——形状(20,1)的偏置矢量
W2——形状的权重矩阵(3,20)
b2——形状(3,1)的偏置矢量
W3——形状(1,3)的权重矩阵
b3——形状(1,1)的偏置矢量
keep_prob——在退出期间保持神经元活动的概率,标量
A3——形状为(1,1)的正向传播输出的最后激活值
cache——元组,为计算反向传播而存储的信息
"""
np.random.seed(1)
# retrieve parameters
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
# Steps 1-4 below correspond to the Steps 1-4 described above.
D1 = np.random.rand(A1.shape[0],A1.shape[1]) # Step 1: initialize matrix D1 = np.random.rand(..., ...)
D1 = D1 < keep_prob # Step 2: convert entries of D1 to 0 or 1 (using keep_prob as the threshold)
A1 = A1 * D1 # Step 3: shut down some neurons of A1
A1 = A1 / keep_prob # Step 4: scale the value of neurons that haven't been shut down
Z2 = np.dot(W2, A1) + b2
A2 = relu(Z2)
D2 = np.random.rand(A2.shape[0],A2.shape[1]) # Step 1: initialize matrix D2 = np.random.rand(..., ...)
D2 = D2 < keep_prob # Step 2: convert entries of D2 to 0 or 1 (using keep_prob as the threshold)
A2 = A2 * D2 # Step 3: shut down some neurons of A2
A2 = A2 / keep_prob # Step 4: scale the value of neurons that haven't been shut down
Z3 = np.dot(W3, A2) + b3
A3 = sigmoid(Z3)
cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)
return A3, cachet_X, parameters = forward_propagation_with_dropout_test_case()
A3, cache = forward_propagation_with_dropout(t_X, parameters, keep_prob=0.7)
print ("A3 = " + str(A3))
forward_propagation_with_dropout_test(forward_propagation_with_dropout)![]()
6.2 带Dropout的后向传播
Exercise 4 - backward_propagation_with_dropout


def backward_propagation_with_dropout(X, Y, cache, keep_prob):
"""
实现我们添加了dropout的基线模型的向后传播。
X——输入数据集,形状(2,示例数)
Y——“真”标签矢量,形状(输出大小,示例数)
cache—从forward_propation_with_dropout()缓存输出
keep_prob——在退出期间保持神经元活动的概率,标量
梯度——关于每个参数、激活和预激活变量的梯度字典
"""
m = X.shape[1]
(Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1./m * np.dot(dZ3, A2.T)
db3 = 1./m * np.sum(dZ3, axis=1, keepdims=True)
dA2 = np.dot(W3.T, dZ3)
dA2 = dA2 * D2 # Step 1: Apply mask D2 to shut down the same neurons as during the forward propagation
dA2 = dA2 / keep_prob # Step 2: Scale the value of neurons that haven't been shut down
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1./m * np.dot(dZ2, A1.T)
db2 = 1./m * np.sum(dZ2, axis=1, keepdims=True)
dA1 = np.dot(W2.T, dZ2)
dA1 = dA1 * D1 # Step 1: Apply mask D1 to shut down the same neurons as during the forward propagation
dA1 = dA1 / keep_prob # Step 2: Scale the value of neurons that haven't been shut down
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1./m * np.dot(dZ1, X.T)
db1 = 1./m * np.sum(dZ1, axis=1, keepdims=True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradientst_X, t_Y, cache = backward_propagation_with_dropout_test_case()
gradients = backward_propagation_with_dropout(t_X, t_Y, cache, keep_prob=0.8)
print ("dA1 = \n" + str(gradients["dA1"]))
print ("dA2 = \n" + str(gradients["dA2"]))
backward_propagation_with_dropout_test(backward_propagation_with_dropout)

parameters = model(train_X, train_Y, keep_prob = 0.86, learning_rate = 0.3)
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)
Dropout效果很好!测试准确率再次提高(达到95%)!您的模型没有过拟合训练集,并且在测试集上做得很好。法国足球队将永远感激你!
运行下面的代码来绘制决策边界。
plt.title("Model with dropout")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
关于Dropout,你应该记住:
Dropout是一种正则化技术。
你只在训练training期间使用。在测试test期间不要使用dropout(随机消除节点)。
在正向和反向传播期间应用丢弃。
在训练时间内,将每个丢失层除以keep_prob,以保持激活的预期值相同。例如,如果keep_prob为0.5,那么我们将平均关闭一半节点,因此输出将按0.5缩放,因为只有剩下的一半对解决方案有贡献。除以0.5等于乘以2。因此,输出现在具有相同的期望值。即使keep_prob为0.5以外的其他值,也可以检查此操作是否有效。
7.总结

请注意,正则化会影响训练集的性能!这是因为它限制了网络过拟合到训练集的能力。但是,由于它最终提供了更好的测试准确性,它正在帮助您的系统。
我们希望您从此笔记本中记住的内容:
正则化将帮助您减少过度拟合。
规则化会使权重降低。
L2正则化和Dropout是两种非常有效的正则化技术。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 让网页自动化测试更简便,流程图设计工具为您解决痛点
- JavaScript 中JSON 字符串和对象之间的转换。
- GB28181/GB35114平台LiveGBS何如添加白名单,使指定海康、大华、华为等GB28181摄像头或录像机设备可以免密接入
- 登录页添加验证码
- ROS常用API(1)
- 限制哪些IP能连接postgre
- 编程笔记 html5&css&js 042 CSS颜色
- 鸿蒙开发-ArkUI框架实战【日历应用 】
- IntelliJ IDEA使用EasyCode插件根据Mysql表自动生成代码文件(controller、service、dao、mapper.xml等)
- C语言编程第二章-C语言程序设计的初步知识(1)