求两个数之间的最小公约数

目录

前言

方法：求两个数之间的最小公约数

1.欧几里得算法

2.枚举法

3.公共因子积

4.更相减损术

5.Stein算法

解题：在链表中插入最大公约数

总结

---

前言

今天刷每日一题：2807. 在链表中插入最大公约数 - 力扣（LeetCode），就在想怎么求两个数之间的最小公约数，然后发现求两个数的最大公约数（五种方法）-CSDN博客

这个博客总结的得很好但也有点自己的想法，于是记录下来，我也是真的超爱写博客了。

---

方法：求两个数之间的最小公约数

1.欧几里得算法

欧几里德算法是用来求两个正整数最大公约数的算法。是由古希腊数学家欧几里德在其著作《The Elements》中最早描述了这种算法,所以被命名为欧几里德算法。

大致过程如下：

1997 / 615 = 3 (余 152)
615 / 152 = 4 (余7)
152 / 7 = 21(余5)
7 / 5 = 1 (余2)
5 / 2 = 2 (余1)
2 / 1 = 2 (余0)

1997 % 615 = 152
615 % 152 = 7
152 % 7 = 5
7 % 5 = 2
5 % 2 = 1
2 % 1 = 0

至此，最大公约数为1。
以除数和余数反复做除法运算，当余数为 0 时，取当前算式除数为最大公约数，所以就得出了 1997 和 615 的最大公约数 1。

观察数就可以得出其算法实现是：

/**
 * 利用 欧几里得算法 求 m 和 n 的最大公约数
 *
 * @param m m
 * @param n n
 * @return m 和 n 的最大公约数
 */
public int gcd(int m, int n) {
    while (n != 0) {
        int temp = m % n;
        m = n;
        n = temp;
    }
    return m;
}

需要注意的是，在参考的博客说m>=n是此算法的必要条件，其实不然，因为就算m<n，经过一次计算后也会使得m>=n，这是算法使然，只是m<n时，这个算法的第一次会失效，重排序去了。因此，m,n可以任意输入。

2.枚举法

给出 m 和 n，首先求出 m 和 n 的最小值赋值给临时变量 t，然后对 t 依次递减，如果 m 除以 t 的余数为 0，并且 n 除以 t 的余数为 0，此时 t 就是 m 和 n 的最大公约数。

这里依然以刚刚的1997和615为例，如果按照枚举法去计算，代码就从t=615依次执行到2，（615-2+1）次，显然效率极低。

算法实现如下:

/**
 * 通过遍历的方式来求 m 和 n 的最大公约数
 *
 * @param m m
 * @param n n
 * @return m 和 n 的最大公约数
 */
public int gcd2(int m, int n) {
    // 第一步:将 min{m, n}的值赋值给 t
    int t = Math.min(m, n);
    for (; t >= 2; t--) {
        // 第二步和第三步,如果 m 除以 t 余数为 0 并且 n 除以 t 余数为 0,直接返回 t
        if (m % t == 0 && n % t == 0) {
            return t;
        }
        // 否则 t--,返回第二步和第三步
    }
    return 1;
}

3.公共因子积

计算两个数字的公共因子积。

第一步:找出 m 的全部质因数
第二步:找出 n 的全部质因数
第三步:从第一步和第二步求得的质因数分解式中找出所有的公因数(如果p是一个公因数,而且在m和n的质因数分解式分别出现过pm和pn 次,那么应该将p重复min{pm, pn}次).
第四步:将第三步中找到的质因数相乘,其结果作为给定数字的最大公约数.

这个太太太繁琐了，完全没必要。看看就得了。

    public int gcd3(int m, int n) {
        Instant start = Instant.now();
        int[] marr = factorArr(m);
        int[] narr = factorArr(n);

        // ---------------------------------------------------------------------
        // 处理两个数组的公共元素
        // ---------------------------------------------------------------------
        // 求出 marr 和 narr 的最大值

        Map<Integer, Integer> mMap = new HashMap<>(marr.length);
        Map<Integer, Integer> nMap = new HashMap<>(narr.length);

        // 处理 marr
        for (int i = 0; i < marr.length; ) {
            int index = i;
            int count = 0;
            while (index < marr.length && marr[index] == marr[i]) {
                count++;
                index++;
            }
            mMap.put(marr[i], count);
            i = index;
        }

        // 处理 narr
        for (int i = 0; i < narr.length; ) {
            int index = i;
            int count = 0;
            while (index < narr.length && narr[index] == narr[i]) {
                count++;
                index++;
            }
            nMap.put(narr[i], count);
            i = index;
        }

        int sum = 1;

        // 可以遍历任意一个 map ，来找出公共元素的个数
        for (Map.Entry<Integer, Integer> entry : mMap.entrySet()) {
            // 取出 value
            int value = entry.getKey();
            // 取出个数
            int count = entry.getValue();
            // 取出另外一个集合中对应 value 值出现的次数
            int anotherCount = nMap.get(value) == null ? 0 : nMap.get(value);
            // 两个因子数组相同因子出现次数的较小值
            int minCount = Math.min(count, anotherCount);

            sum *= minCount * value == 0 ? 1 : Math.pow(value, minCount);
        }

        return sum;
    }

    /**
     * 返回 value 的全部因子,以数组的形式返回
     *
     * @param value value 值
     * @return value 的全部因子,以数组的形式返回
     */
    private int[] factorArr(int value) {
        List<Integer> list = new ArrayList<>();
        for (int i = 2; i <= Math.sqrt(value); i++) {
            if (value % i == 0) {
                list.add(i);
                value /= i;
                i--;
            }
        }
        return list.stream().mapToInt(Integer::valueOf).toArray();
    }

4.更相减损术

• 第一步：任意给定两个正整数；判断它们是否都是偶数。若是，则用2约简；若不是则执行第二步。
• 第二步：以较大的数减较小的数，接着把所得的差与较小的数比较，并以大数减小数。继续这个操作，直到所得的减数和差相等为止。
• 则第一步中约掉的若干个2的积与第二步中等数的乘积就是所求的最大公约数。

/**
 * 使用更相减损法求 m 和 n 的最大公约数
 *
 * @param m 数字 m
 * @param n 数字 n
 * @return m 和 n 的最大公约数
 */
public int gcd4(int m, int n) {
    // 两个数字不相等时，继续进行运算，
    while (m != n) {
        if (m > n) m -= n;
        else n -= m;
    }
    return m;
}

这个也很简洁，但也没有取余来得高效。

5.Stein算法

欧几里德算法是计算两个数最大公约数的传统算法，无论从理论还是从实际效率上都是很好的。但是却有一个致命的缺陷，这个缺陷在素数比较小的时候一般是感觉不到的，只有在大素数时才会显现出来：一般实际应用中的整数很少会超过64位（当然现在已经允许128位了），对于这样的整数，计算两个数之间的模是很简单的。对于字长为32位的平台，计算两个不超过32位的整数的模，只需要一个指令周期，而计算64位以下的整数模，也不过几个周期而已。但是对于更大的素数，这样的计算过程就不得不由用户来设计，为了计算两个超过64位的整数的模，用户也许不得不采用类似于多位数除法手算过程中的试商法，这个过程不但复杂，而且消耗了很多CPU时间。对于现代密码算法，要求计算128位以上的素数的情况比比皆是，比如说RSA加密算法至少要求500bit密钥长度，设计这样的程序迫切希望能够抛弃除法和取模。
Stein算法很好的解决了欧几里德算法中的这个缺陷，Stein算法只有整数的移位和加减法。

讲实话，这个我还没搞得太懂，需要之后好好看看，对于较大数字用这个。

递归：

/**
 * 求两个正整数的最大公因数
 * <p>
 * 结合辗转相除法和更相减损法的优势以及移位运算
 * 
 * 结合辗转相除法和更相减损法的优势以及移位运算
 * 对 m 和 n 分四种情况
 * 如果 m 为偶数 n 为偶数, gcd(m, n) = gcd(m >> 1, n >> 1) << 1;
 * 如果 m 为偶数 n 为奇数, gcd(m, n) = gcd(m >> 1, n);
 * 如果 m 为奇数 n 为偶数, gcd(m, n) = gcd(m, n >> 1);
 * 如果 m 为奇数 n 为奇数, gcd(m, n) = gcd(n, m - n);
 *
 * @param m 数字 m
 * @param n 数字 n
 * @return 返回 m 和 n 的最大公因数
 */
public int gcd5(int m, int n) {
    // 这个地方也是利用到更相减损术
    if (m == n) {
        return m;
    }
    // 为了保证较大的数始终在前面，减少了代码
    if (n > m) {
        return gcd5(n, m);
    } else {
        if (((m & 1) == 0) && ((n & 1) == 0)) {
            // 两数都是偶数
            return gcd5(m >> 1, n >> 1) << 1;
        } else if ((m & 1) == 0 && (n & 1) != 0) {
            // m为偶数，n为奇数
            return gcd5(m >> 1, n);
        } else if ((m & 1) != 0 && (n & 1) == 0) {
            // m为奇数，n为偶数
            return gcd5(m, n >> 1);
        } else {
            // 当两个数都为奇数时，应用更相减损法
            // 这个位置利用到了更相减损术
            return gcd5(n, m - n);
        }
    }
}

非递归：

/**
 * Stein 算法的非递归实现
 * 
 * @param m m
 * @param n n
 * @return  m 和 n 的最大公因子
 */
public int steinGCD(int m, int n) {
    int count = 0;
    if (m < n) return steinGCD(n , m);
    while ((m & 1) == 0 && (n & 1) == 0) {
        count++;
        m >>= 1;
        n >>= 1;
    }
    while (m != n) {
        while ((m & 1) == 0) m >>= 1;
        while ((n & 1) == 0) n >>= 1;
        if (m < n) {
            m ^= n;
            n ^= m;
            m ^= n;
        }
        // 进行一次更相减损术
        int temp = m - n;
        m = n;
        n = temp;
    }
    return m << count;
}

解题：在链表中插入最大公约数

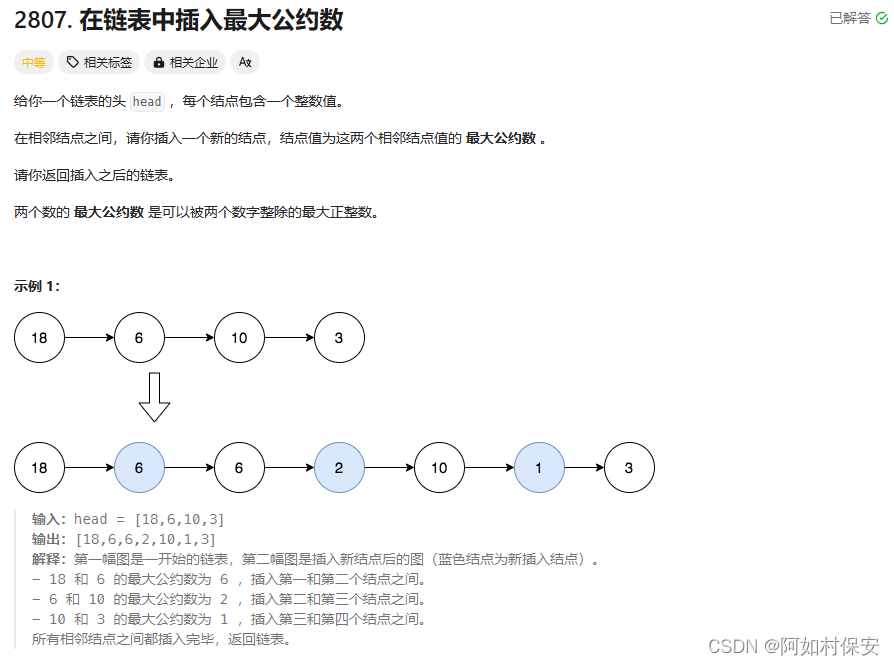
?这里链表插入删除的逻辑还是很好做的，要注意的是这个while的条件：current != null && current.next != null

这里的gcd函数就是用来求最小公约数的（刚说的几种都可试试）。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode insertGreatestCommonDivisors(ListNode head) {
        ListNode current = head;

        while (current != null && current.next != null) {
            ListNode next = current.next;
            int gcdValue = gcd(current.val, next.val);

            // 在相邻节点之间插入新节点
            ListNode newNode = new ListNode(gcdValue);
            newNode.next = next;
            current.next = newNode;

            // 更新 current 指针到下一个相邻节点
            current = next;
        }

        return head;
    }

    /**
     * 计算两个数的最大公约数
     *
     * @param a 第一个数
     * @param b 第二个数
     * @return 最大公约数
     */
    private int gcd(int a, int b) {
        while (b != 0) {
            int temp = a % b;
            a = b;
            b = temp;
        }
        return a;
    }
}

---

总结

?当数较小时（不超过64位），用欧几里得算法（取余）或者更相减损术；当数太大时，用stein算法，此算法只有整数的移位和加减法。

加油加油，今天熬熬夜。