权重衰减(Weight Decay)
???????在深度学习中,权重衰减(Weight Decay)是一种常用的正则化技术,旨在减少模型的过拟合现象。权重衰减通过向损失函数添加一个正则化项,以惩罚模型中较大的权重值。
一、权重衰减
???????在深度学习中,模型的训练过程通常使用梯度下降法(或其变种)来最小化损失函数。梯度下降法的目标是找到损失函数的局部最小值,使得模型的预测能力最好。然而,当模型的参数(即权重)过多或过大时,容易导致过拟合问题,即模型在训练集上表现很好,但在测试集上表现较差。
???????权重衰减通过在损失函数中引入正则化项来解决过拟合问题。正则化项通常使用L1范数或L2范数来度量模型的复杂度。L2范数正则化(也称为权重衰减)是指将模型的权重的平方和添加到损失函数中,乘以一个较小的正则化参数。这个额外的项迫使模型学习到较小的权重值,从而减少模型的复杂度。
???????具体而言,对于一个深度学习模型的损失函数,其中
表示模型的参数(权重和偏置),权重衰减可以通过以下方式实现:
???????其中,是添加了权重衰减的损失函数,
表示参数的L2范数的平方和,
是正则化参数,用于控制正则化项的重要性。
???????在训练过程中,梯度下降法将同时更新损失函数和权重。当计算梯度时,权重衰衰减的正则化项将被添加到梯度中,从而导致权重更新的幅度减小。这使得模型的权重趋向于减小,避免过拟合现象。
???????需要注意的是,正则化参数的选择对模型的性能有重要影响。较小的
值会导致较强的正则化效果,可能会使模型欠拟合。而较大的
值可能会减少正则化效果,使模型过拟合。因此,选择合适的正则化参数是权衡模型复杂度和泛化能力的关键。
???????偏置(biases)在神经网络中起到平移激活函数的作用,通常不会像权重那样导致过度拟合。偏置的主要作用是调整激活函数的位置,使其更好地对应所需的输出。由于偏置的影响较小,因此将权重衰减应用于偏置通常不是常见的做法。
二、权重衰减数学解释
???????L2范数正则化在解决过拟合问题方面具有一定的效果,这是因为它在损失函数中引入了权重的平方和作为正则化项。下面我将解释一下L2范数正则化的数学原理。
???????在深度学习中,我们的目标是最小化损失函数,该函数包括两部分:经验误差和正则化项。对于L2范数正则化,我们将正则化项定义为权重的平方和的乘以一个正则化参数。
???????针对损失函数,我们使用梯度下降法来最小化这个损失函数。在梯度下降的每一步中,我们计算损失函数的梯度,然后更新权重。对于L2范数正则化,梯度的计算中包含了正则化项的贡献。
???????具体来说,我们计算损失函数对权重w的梯度,记为。那么加入L2范数正则化后的梯度可以写为:
???????这里,是正则化项的梯度贡献,其中
是正则化参数
的倍数,
是权重的梯度。
???????当我们使用梯度下降法更新权重时,梯度的负方向指示了损失函数下降的方向。由于L2范数正则化项的存在,权重的梯度会受到惩罚,从而导致权重的更新幅度减小。
???????这种减小权重更新幅度的效果使得模型倾向于学习到较小的权重值,从而降低了模型的复杂度。通过减小权重的幅度,L2范数正则化可以有效地控制模型的过拟合,提高模型的泛化能力。
???????总结起来,L2范数正则化通过引入权重的平方和作为正则化项,在梯度计算和权重更新中对权重进行惩罚,从而减小了模型的复杂度,防止过拟合现象的发生。
也可以参考李沐老师的课件:
三、代码从零开始实现
import torch
from torch import nn
from d2l import torch as d2l1、生成数据
???????首先,我们像以前一样生成一些数据,生成公式如下:
???????我们选择标签是关于输入的线性函数。标签同时被均值为0,标准差为0.01高斯噪声破坏。为了使过拟合的效果更加明显,我们可以将问题的维数增加到(w的长度为200),并使用一个只包含20个样本的小训练集。
n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5 # 训练集长度为20、验证机长度为100、权重参数有200个、批量大小为5
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05 # 真实的权重和偏置
train_data = d2l.synthetic_data(true_w, true_b, n_train)
train_iter = d2l.load_array(train_data, batch_size)
test_data = d2l.synthetic_data(true_w, true_b, n_test)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)2、初始化模型参数
???????我们将定义一个函数来随机初始化模型参数。
def init_params():
w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
return [w, b]3、定义L2范数惩罚
???????实现这一惩罚最方便的方法是对所有项求平方后并将它们求和。
def l2_penalty(w):
return torch.sum(w.pow(2)) / 24、定义训练代码实现
???????下面的代码将模型拟合训练数据集,并在测试数据集上进行评估。和之前线性回归一样,线性网络和平方损失没有变化,所以我们通过`d2l.linreg`和`d2l.squared_loss`导入它们。唯一的变化是损失现在包括了惩罚项。
def train(lambd):
w, b = init_params()
net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss
num_epochs, lr = 100, 0.003
animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
xlim=[5, num_epochs], legend=['train', 'test'])
for epoch in range(num_epochs):
for X, y in train_iter:
# 增加了L2范数惩罚项,
# 广播机制使l2_penalty(w)成为一个长度为batch_size的向量
l = loss(net(X), y) + lambd * l2_penalty(w)
l.sum().backward()
d2l.sgd([w, b], lr, batch_size)
if (epoch + 1) % 5 == 0:
animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
d2l.evaluate_loss(net, test_iter, loss)))
print('w的L2范数是:', torch.norm(w).item())5、忽略正则化直接训练
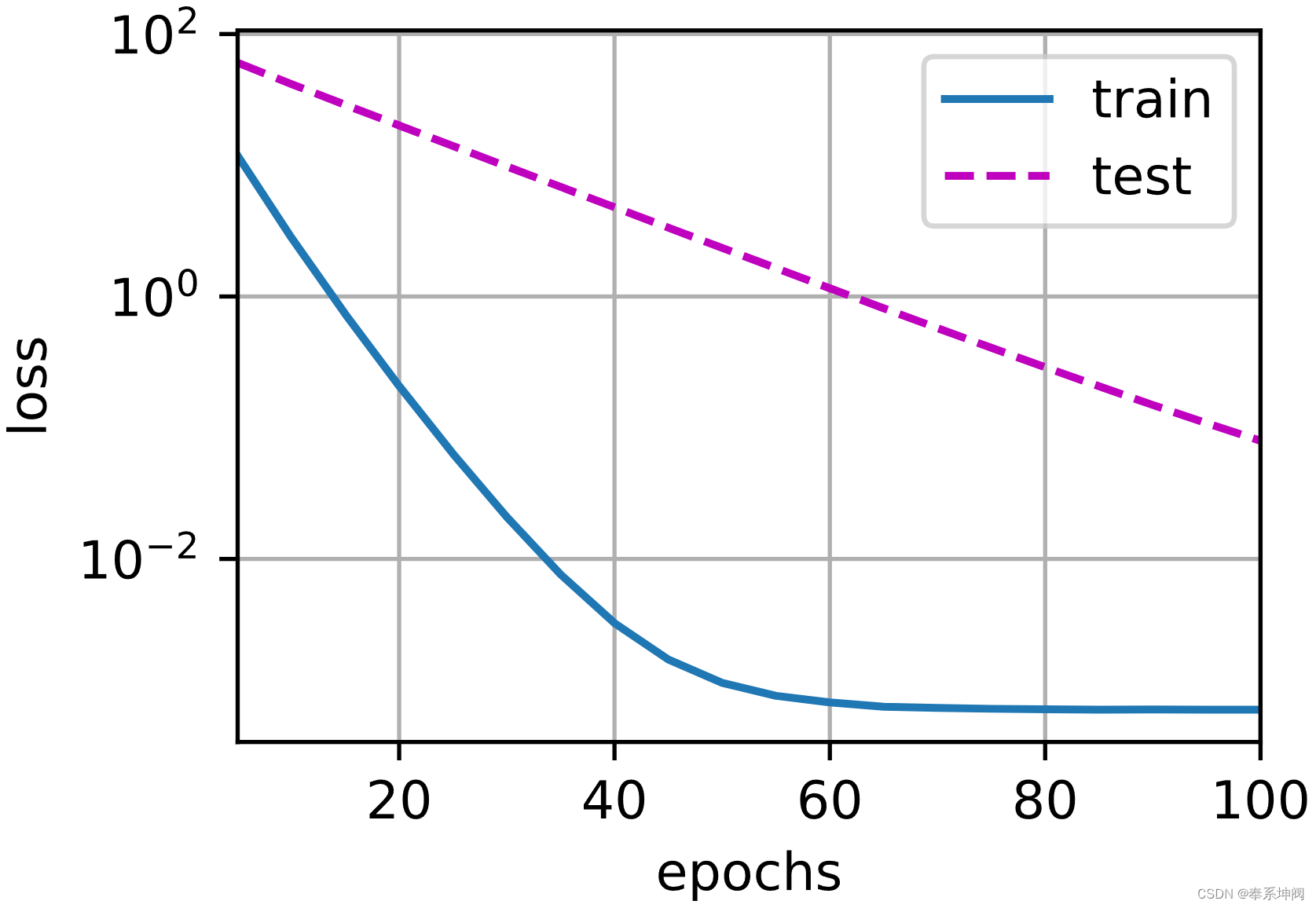
???????我们现在用`lambd = 0`禁用权重衰减后运行这个代码。注意,这里训练误差有了减少,但测试误差没有减少,这意味着出现了严重的过拟合。
train(lambd=0)w的L2范数是: 12.963241577148438?

6、使用权重衰减
???????下面,我们使用权重衰减来运行代码。注意,在这里训练误差增大,但测试误差减小。这正是我们期望从正则化中得到的效果。
train(lambd=3)w的L2范数是: 0.3556520938873291?
四、简洁实现
???????由于权重衰减在神经网络优化中很常用,深度学习框架为了便于我们使用权重衰减,将权重衰减集成到优化算法中,以便与任何损失函数结合使用。此外,这种集成还有计算上的好处,允许在不增加任何额外的计算开销的情况下向算法中添加权重衰减。由于更新的权重衰减部分仅依赖于每个参数的当前值,因此优化器必须至少接触每个参数一次。
1、定义训练代码实现
???????在下面的代码中,我们在实例化优化器时直接通过`weight_decay`指定weight decay超参数。默认情况下,PyTorch同时衰减权重和偏移。这里我们只为权重设置了`weight_decay`,所以偏置参数不会衰减。
def train_concise(wd):
net = nn.Sequential(nn.Linear(num_inputs, 1))
for param in net.parameters():
param.data.normal_()
loss = nn.MSELoss(reduction='none')
num_epochs, lr = 100, 0.003
# 偏置参数没有衰减
trainer = torch.optim.SGD([{"params":net[0].weight,'weight_decay': wd}, {"params":net[0].bias}],
lr=lr)
animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
xlim=[5, num_epochs], legend=['train', 'test'])
for epoch in range(num_epochs):
for X, y in train_iter:
trainer.zero_grad()
l = loss(net(X), y)
l.mean().backward()
trainer.step()
if (epoch + 1) % 5 == 0:
animator.add(epoch + 1,
(d2l.evaluate_loss(net, train_iter, loss),
d2l.evaluate_loss(net, test_iter, loss)))
print('w的L2范数:', net[0].weight.norm().item())2、忽略正则化直接训练
train_concise(0)w的L2范数: 13.727912902832031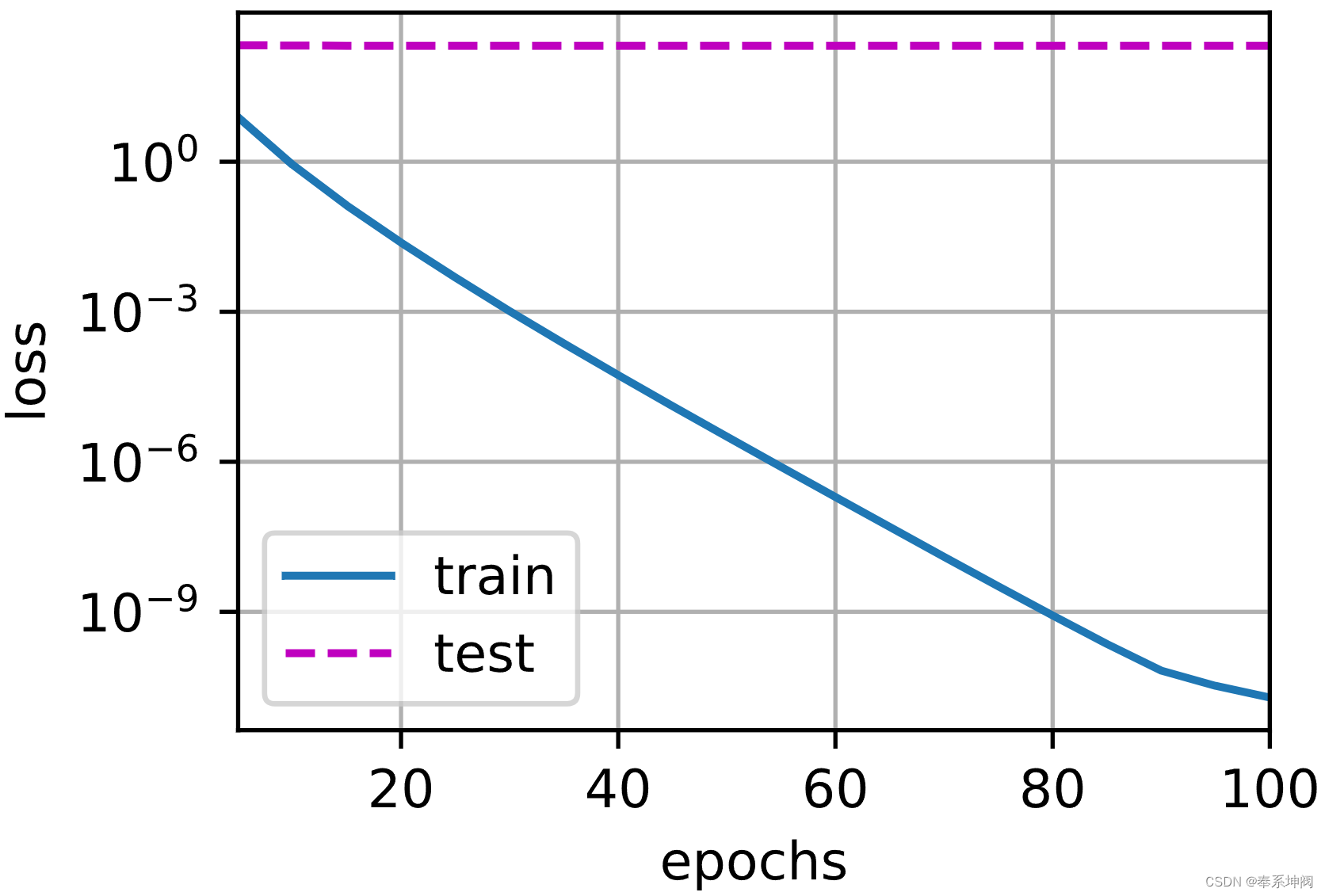
3、使用权重衰减
train_concise(3)w的L2范数: 0.3890590965747833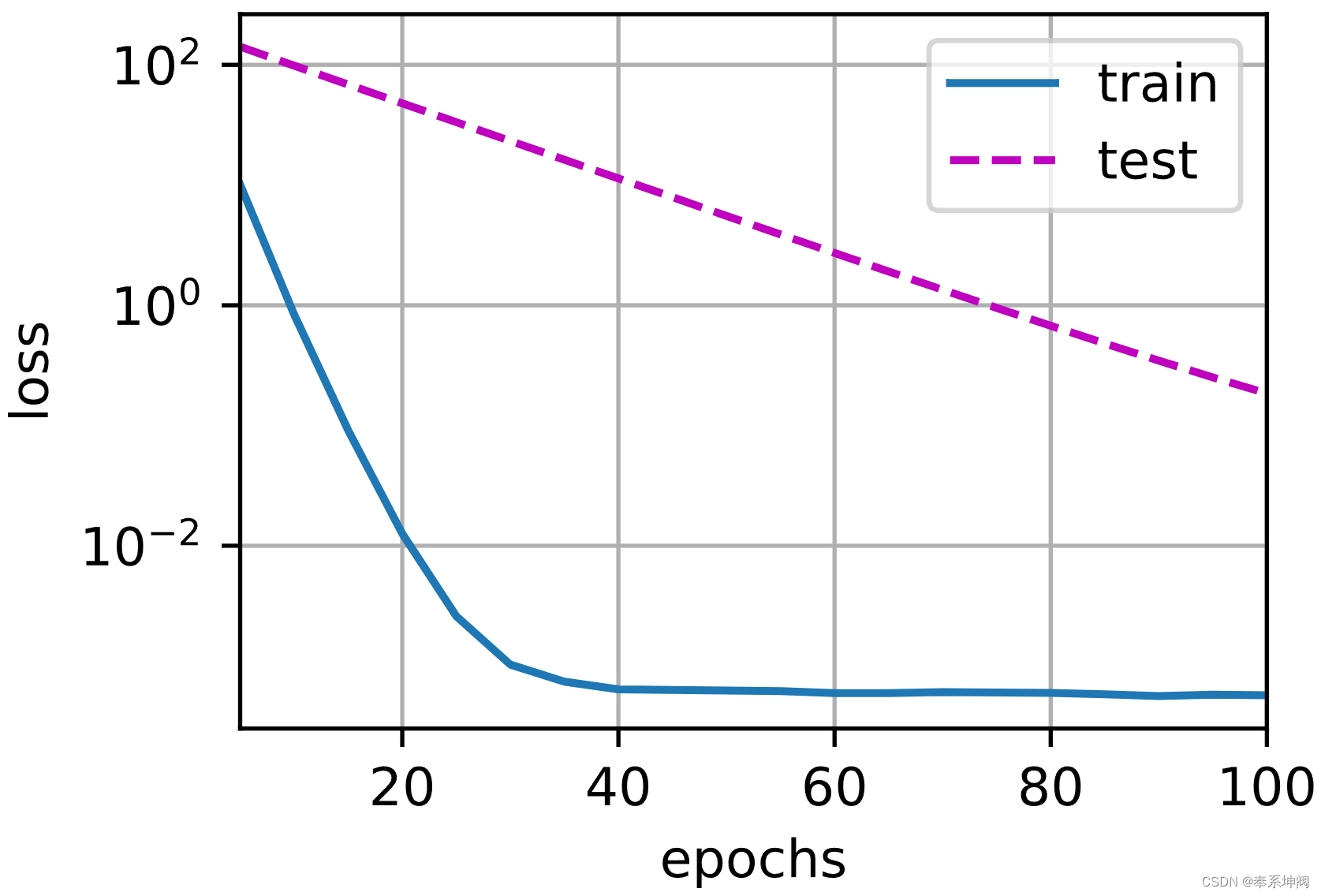
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 如何通过易舟云财务软件,进行结转结账?
- HarmonyOS应用开发学习笔记 UIAbility组件与UI的数据同步 EventHub、globalThis
- 零基础学C语言——学前准备
- Windows内存取证
- 基于PID神经网络的系统控制(附带Matlab代码)
- sizeof和strlen的对比
- 红日靶场之sta&&ck远程桌面控制 个人学习)
- 全局变量可不可以定义在可被多个.C?件包含的头?件中?为什么?
- 【RTOS】快速体验FreeRTOS所有常用API(1)工程创建
- StopWatch



