【排序】快速排序
发布时间:2024年01月10日
思想
快速排序是一种基于分治策略的排序算法,其核心思想通过选取一个基准元素,将数组分成两个子数组:一个包含小于基准元素的值,另一个包含大于基准元素的值。然后递归地对这两个子数组进行排序,最终将它们合并起来,得到有序的数组。
图解实现
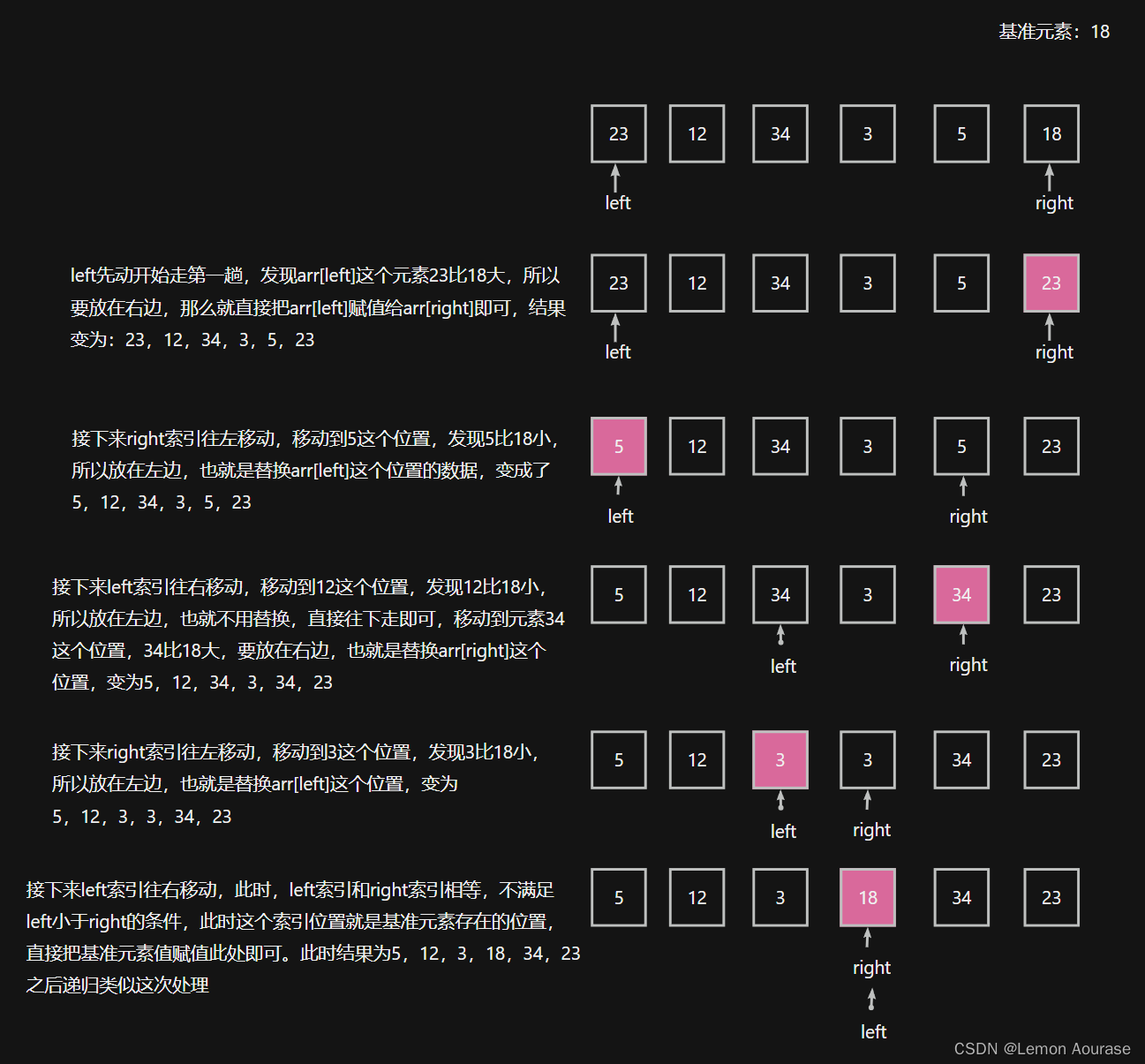
具体代码实现
public static int[] quickSort(int[] arr, int leftIndex, int rightIndex) {
// 递归结束条件 左边索引小于右边索引
if (leftIndex < rightIndex) {
// 通过分区函数得到基准元素的索引
int pivotIndex = partition(arr, leftIndex, rightIndex);
//递归对基准元素左边的子数组进行快速排序
quickSort(arr, leftIndex, pivotIndex - 1);
//递归对基准元素右边的子数组进行快速排序
quickSort(arr, pivotIndex + 1, rightIndex);
}
return arr;
}
/**
* 分区函数
*
* @param arr 数组
* @param leftIndex 左索引
* @param rightIndex 右索引
* @return 返回基准元素的索引
*/
private static int partition(int[] arr, int leftIndex, int rightIndex) {
// 基准元素是最后一个元素
int baseNum = arr[rightIndex];
// 左边索引小于右边索引就一直循环
while (leftIndex < rightIndex) {
// l < r 且 左边的元素一直小于基准元素,左边索引做加1操作(因为要放在基准元素左边)
while (leftIndex < rightIndex && arr[leftIndex] <= baseNum) {
leftIndex++;
}
// 如果不满足上边条件,说明此时这个值要比基准元素大,就放在基准元素右边。把左边元素值直接赋给右边即可(注意基准元素全局不参与运算,存在的意义只是比较而已)
arr[rightIndex] = arr[leftIndex];
// l < r 且 右边的元素一直大于基准元素,右边索引做减1操作(因为要放在基准元素右边)
while (leftIndex < rightIndex && arr[rightIndex] >= baseNum) {
rightIndex--;
}
// 如果不满足上边条件,说明此时这个值要比基准元素小,就放在基准元素左边。把右边元素值直接赋给左边即可
arr[leftIndex] = arr[rightIndex];
}
// 走到这里说明 leftIndex < rightIndex 这个条件就不满足了,也就是说 leftIndex = rightIndex,这个时候把基准元素的值复制在这个位置即可,
// 并返回此时这个位置的索引即可。
arr[leftIndex] = baseNum;
return leftIndex;
}
建议
仔细看那个图解思路实现,先把思路搞清楚,然后写代码具体实现。别人写的代码终究是别人理解之后写出来的,要搞明白其中思路。一定一定要多动手实现,多写代码,多Debug。
纸上得来终觉浅,绝知此事要躬行
参考链接
文章来源:https://blog.csdn.net/weixin_44078354/article/details/135410918
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 尺寸链计算软件-产品功能及优势-DTAS3D自主可控
- 基于深度学习的PCB板缺陷检测系统(含UI界面、yolov5、Python代码、数据集)
- 15:00面试,15:06就出来了,问的问题有点变态。。。
- 公众号突破2个限制技巧怎么操作?
- 山海鲸可视化:开启生命科学探索新篇章
- C# 实时存储16进制数据,写入文件格式为Raw
- [Mac软件]App Cleaner & Uninstaller 8.2.5应用程序清理和卸载
- 【Java】工业园区高精准UWB定位系统源码
- “PowerTransmissionLoss“app Tech Support(URL)
- vivado 工程管理