力扣200. 岛屿数量(java DFS解法)
Problem: 200. 岛屿数量
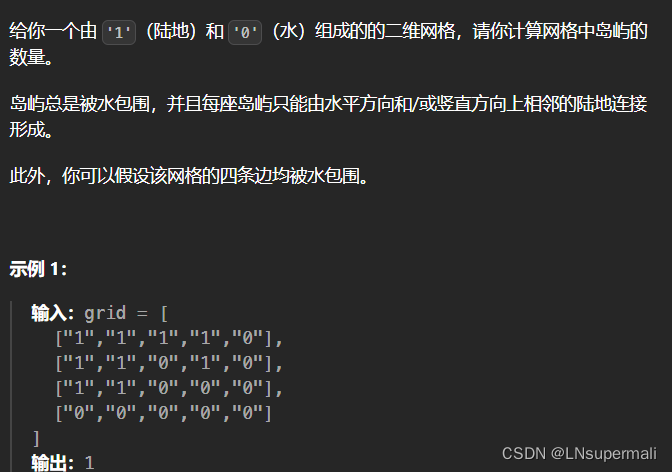
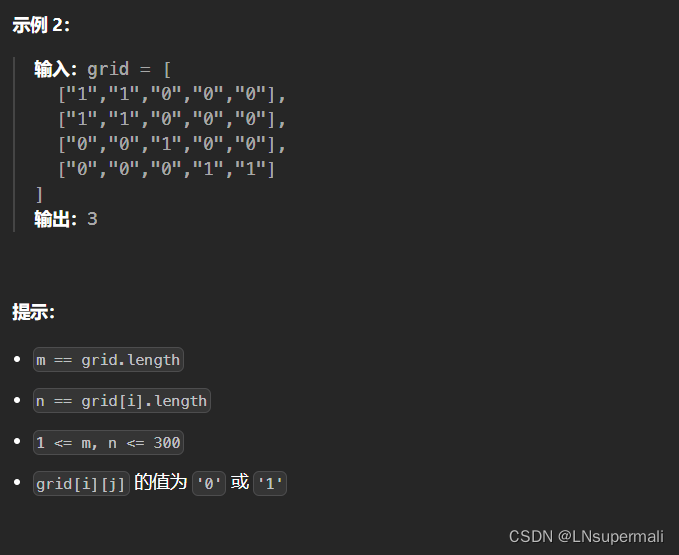
题目描述
思路
该问题可以归纳为一类遍历二维矩阵的题目,此类中的一部分题目可以利用DFS来解决,具体到本题目:
1.我们首先要针对于二维数组上的每一个点,尝试展开DFS
2.我们定义一个和给定矩阵一样大的布尔类型的矩阵visited,用于辅助判断是否开展DFS,若是符合的合法点,则设置为true
3.我们在DFS的具体实现中,以每一个点为基础,从该点的上下左右四个方位开始尝试是否DFS
解题方法
1.定义二维辅助数组visited初始化大小为给定数组grid的大小(若在后续操作中标记某一点为true则表示该位置是已经遍历过的合法位置),定义记录岛屿数量的变量count
2.在主函数(numIslands)中我们遍历二维数组中每一个点,当满足visited[i][j] != true && grid[i][j] == '1’时,则代表此处最少存在一个岛屿count加一,再调用DFS函数
3.DFS函数的具体处理:3.1 每次先将当前合法位置设置为true(visited中),定义一个二维数组**int[][] directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};用于记录当前某一位置的点的四个方位(上下左右)
3.2 for循环(范围1~4),循环中每次执行 int newI = i + directions[k][0];int newJ = j + directions[k][1];**用于记录当前位置的新的位置,并判断当前新位置是否合法,若合法则DFS递归调用(在新的位置的基础上)
复杂度
时间复杂度:
O ( m n ) O(mn) O(mn)
空间复杂度:
O ( m n ) O(mn) O(mn)
Code
class Solution {
private boolean[][] visited;
private int row;
private int col;
/**
* Get all the island counts
*
* @param grid Given a two-dimensional array
* @return int
*/
public int numIslands(char[][] grid) {
row = grid.length;
col = grid[0].length;
visited = new boolean[row][col];
//The count of island
int count = 0;
for (int i = 0; i < row; ++i) {
for (int j = 0; j < col; ++j) {
if (visited[i][j] != true && grid[i][j] == '1') {
count++;
dfs(grid, i, j);
}
}
}
return count;
}
/**
* Try dfs or not from each point in a two-dimensional array
*
* @param grid Given a two-dimensional array
* @param i Abscissa
* @param j Ordinate
*/
private void dfs(char[][] grid, int i, int j) {
//Record four bearings
int[][] directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
//The current legal location is set to true
visited[i][j] = true;
for (int k = 0; k < 4; ++k) {
int newI = i + directions[k][0];
int newJ = j + directions[k][1];
if (newI >= 0 && newI < row && newJ >= 0 && newJ < col
&& visited[newI][newJ] == false && grid[newI][newJ] == '1') {
dfs(grid, newI, newJ);
}
}
}
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 用pthon 实现电脑性能监控并把监控数据写入excel
- 探索“城堡世界”APP:打造你的梦幻城堡
- 【C++ 程序设计入门基础】- 第4节-函数
- 16 定时器中断
- C++模板类与Java泛型类的实战应用及对比分析
- Linux mesg命令教程:如何控制终端的消息接收(附案例详解和注意事项)
- 第五章 SpringBoot实现Web的常用功能
- qt:使用信号槽机制传参
- SQL注入入门进阶_报错注入、延时注入、python脚本盲注
- 什么是Vue.js ? Vue相关介绍