EI论文复现：主动配电网最优潮流研究及其应用实例程序代码！

适用平台及主要参考论文：Matlab+Yalmip+Cplex/Gurobi；

《主动配电网最优潮流研究及其应用实例》；

程序建立了基于二阶锥松弛的配电网动态最优潮流模型(SOCR-DOPF)框架，并对主动配电网各参与元素(如有载调压变压器(on—load tap changer，OLTC)，储能系统(energy storage system，ESS)等)关键约束的线性建模处理方法进行相应的探索，进而将配电网非线性最优潮流问题转化为基于二阶锥规划进行快速求解。同时，对网络辐射性和连通性约束限制也进行了充分说明。程序中算例丰富、注释清晰、干货满满，创新性很高！下面对文章和程序做简要介绍！

文章创新点：

主动配电网；动态最优潮流；二阶锥松弛；配电网重构；综合负荷

主要工作：

最优潮流研究在配电网规划运行中不可或缺，且在大量分布式能源接入的主动配电网环境下尤为重要。传统的启发式算法在全局最优解和求解速度上均无法满足主动配电网运行要求，而基于线性化的最优潮流方法在高阻抗的配电网中适用性也较弱。基于此，文章建立了基于二阶锥规划(second order cone programming，SOCP)的动态最优潮流模型框架，力图将原非线性规划模型松弛转化为SOCP进行快速求解。首先，给出了基于二阶锥松弛的配电网动态最优潮流基本模型；然后，对主动配电网中各重要参与元素进行相应的线性化建模处理 以便高效求解，如主动管理设备、配电网重构、需求响应及综合负荷等；同时，分析了松弛模型和近似等效的准确性。

?程序结果：

?(1)单时段：

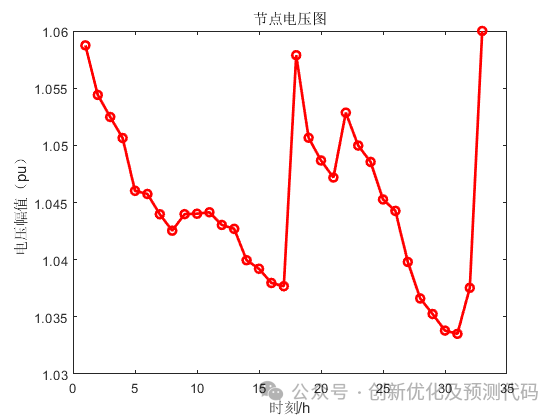
（2）?多时段：

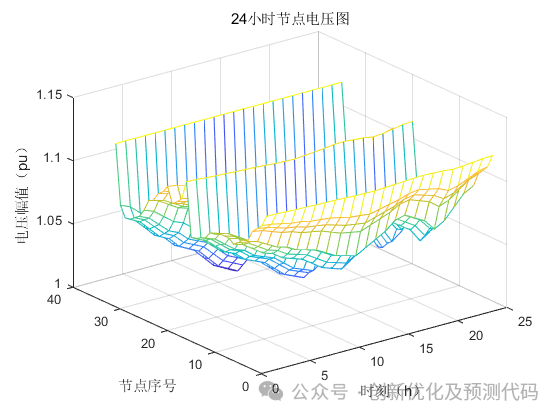
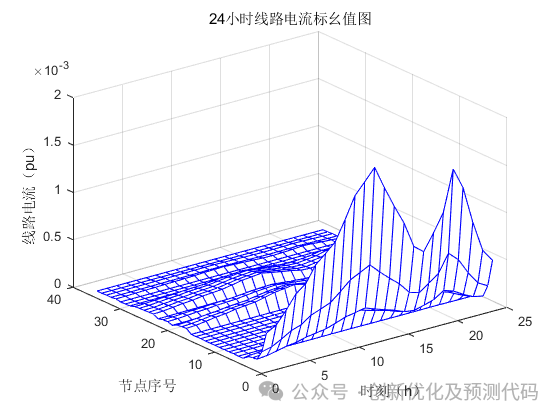
?部分程序：

%% 1.设参
mpc = IEEE33BW;
pload = mpc.Pload;%节点有功负荷
qload = mpc.Qload;%节点无功负荷
branch = mpc.branch_CG;         
branch(:,3) = branch(:,3)*100/(12.66^2);%求阻抗标幺值
r=real(branch(:,3));         
x=imag(branch(:,3));            

T = 24;%时段数为24小时
nb = 33;%节点数,根节点为33
nl = 37;%支路数
nc = 5;%联络开关数

upstream=zeros(nb,nl);%代表流入节点支路
dnstream=zeros(nb,nl);%代表流出节点支路
for i=1:32
    upstream(i,i)=1;
end
upstream(20,33)=1;%支路33为20-7支路，流入节点20
upstream(14,34)=1;%支路34为14-8支路，流入节点14
upstream(21,35)=1;%支路35为21-11支路，流入节点21
upstream(32,36)=1;%支路36为32-17支路，流入节点32
upstream(28,37)=1;%支路37为28-24支路，流入节点28

for i=[1:16,18:20,22:23,25:31]
    dnstream(i,i+1)=1;
end
dnstream(1,18)=1;
dnstream(2,22)=1;
dnstream(5,25)=1;
dnstream(33,1)=1;
%5条流入，对应5条流出
dnstream(7,33)=1;
dnstream(8,34)=1;
dnstream(11,35)=1;
dnstream(17,36)=1;
dnstream(24,37)=1;

Vmax=[1.06*1.06*ones(32,T);1.06*1.06*ones(1,T)];
Vmin=[0.94*0.94*ones(32,T);1.06*1.06*ones(1,T)];
Pgmax=[zeros(32,T);ones(1,T)];
Qgmax=[zeros(32,T);ones(1,T)];

%% 2.设变量
V = sdpvar(nb,T);%电压的平方
I = sdpvar(nl,T);%电流的平方
P = sdpvar(nl,T);%线路有功
Q = sdpvar(nl,T);%线路无功
Pg = sdpvar(nb,T);%发电机有功
Qg = sdpvar(nb,T);%发电机无功

Zij=binvar(nl,1);%网架结构               
Z0=[ones(nl-nc,1);zeros(nc,1)];%初始拓扑                      
assign(Zij,Z0);          

%% 3.设约束
Constraints = [];           
%% 网络重构约束
Constraints = [Constraints, sum(Zij) == 32];                
%提高运算速度            
Constraints = [Constraints, Zij(1,1) == 1];         %这里可以确定的是，与主网相连的路一定是闭合的，所以可以提前置1，使运算更加快速 
%分出12个section   将支路捆绑，然后设定其中多条串接的支路至多有一条断开      
s1=3;s2=2;s3=1;s4=3;s5=3;s6=8;s7=4;s8=1;s9=2;s10=4;s11=4;s12=1;              
Constraints = [Constraints, s1-sum(Zij(3:5)) <=1,s2-sum(Zij(6:7)) <=1];
Constraints = [Constraints, s4-sum(Zij(9:11)) <=1,s5-sum(Zij(12:14)) <=1];
Constraints = [Constraints, s6-sum(Zij(15:17))-sum(Zij(29:32))-sum(Zij(36))<=1];
Constraints = [Constraints, s7-sum(Zij(18:20))-sum(Zij(2))<=1,s9-sum(Zij(21))-sum(Zij(35))<=1];
Constraints = [Constraints, s10-sum(Zij(22:24))-sum(Zij(37))<=1,s11-sum(Zij(25:28))];

% P_tree = sdpvar(37,1);%虚拟有功
% Pin_tree = -upstream*P_tree + dnstream*P_tree;%虚拟节点注入有功
% Constraints = [Constraints,-Zij <= P_tree <= Zij];
% Constraints = [Constraints, Pin_tree(1:32) + 0.01==0];
%% 潮流约束
%节点功率约束
Pin = upstream*P - upstream*(I.*(r*ones(1,T))) - dnstream*P;%节点注入有功
Qin = upstream*Q - upstream*(I.*(x*ones(1,T))) - dnstream*Q;%节点注入无功
Constraints = [Constraints, Pin  + Pg== pload];
Constraints = [Constraints, Qin  + Qg== qload];
%欧姆定律约束
m = 1.06*1.06 - 0.94*0.94;
M = (ones(nl,T) - Zij*ones(1,T))*m;             
Constraints = [Constraints, V(branch(:,1),:) - V(branch(:,2),:) <= M + 2*(r*ones(1,T)).*P + 2*(x*ones(1,T)).*Q - ((r.^2 + x.^2))*ones(1,T).*I];
Constraints = [Constraints, V(branch(:,1),:) - V(branch(:,2),:) >= -M + 2*(r*ones(1,T)).*P + 2*(x*ones(1,T)).*Q - ((r.^2 + x.^2))*ones(1,T).*I];
%二阶锥约束                 
Constraints = [Constraints, V(branch(:,1),:).*I >= P.^2+Q.^2];          
%% 通用约束

%节点电压约束               
Constraints = [Constraints, Vmin <= V,V <= Vmax];             
%发电机功率约束           
Constraints = [Constraints, -Pgmax <= Pg,Pg <= Pgmax,-Qgmax <= Qg,Qg <= Qgmax];
%支路电流约束
Constraints = [Constraints, 0 <= I,I <= 0.11*Zij*ones(1,T)];
%支路功率约束
Constraints = [Constraints, -0.11*Zij*ones(1,T) <= P,P <= 0.11*Zij*ones(1,T),-0.11*Zij*ones(1,T) <= Q,Q <= 0.11*Zij*ones(1,T)];

欢迎感兴趣的小伙伴关注，小编会不定期更新高质量的学习资料、文章和程序代码，为您的科研加油助力！