【图像分类】【深度学习】【轻量级网络】【Pytorch版本】EfficientNet_V1模型算法详解

【图像分类】【深度学习】【轻量级网络】【Pytorch版本】EfficientNet_V1模型算法详解

---

前言

EfficientNet_V1是由谷歌公司的Tan, Mingxing等人《EfficientNet:Rethinking Model Scaling for Convolutional Neural Networks【ICML-2019】》【论文地址】一文中提出的模型，通过复合缩放把网络缩放的深度、宽度和分辨率组合起来按照一定规则缩放，从而提高网络的效果。

---

EfficientNet_V1讲解

卷积神经网络通常是在固定的资源预算下开发的，如果有更多的资源可用，那么卷积神经网络就可以扩展以获得更好的精度。目前有许多方法可以做到这一点，最常见的方法是按其深度或宽度扩大卷积神经网络，另一种不太常见但越来越流行的方法是通过扩大图像分辨率扩大模型。在以前的工作中，通常只缩放三个维度中的一个—深度、宽度和图像大小。虽然可以任意缩放二维或三维，但任意缩放需要冗长的手动调整，而且通常会产生次优的精度和效率。因此，本论文对卷积神经网络的扩展过程进行了研究和反思，系统地研究了模型缩放，并发现仔细平衡网络深度、宽度和分辨率可以获得更好的性能。基于这一观察提出了一种新的缩放方法，该方法使用一个简单但高效的复合系数统一缩放深度/宽度/分辨率的所有尺寸。
以下是原论文提出的缩放方法和传统方法之间的区别的示意图：

研究的核心问题：是否有一个理论性的方法来扩展卷积神经网络，以实现更好的准确性和效率？
平衡网络宽度/深度/分辨率的所有维度是至关重要的，这种平衡可以通过简单地用恒定比率缩放每个维度来实现，因此论文提出了一种简单而有效的复合缩放法，使用一组固定的缩放系数统一缩放网络宽度、深度和分辨率。例如，如果我们想使用$2^N$倍以上的计算资源，那么我们可以简单地将网络深度增加${\alpha }^N$，宽度增加${\beta }^N$，图像大小增加${\gamma }^N$，其中$\alpha$，$\beta$，$\gamma$是由原始小模型上的小网格搜索确定的常数系数。论文使用神经架构搜索来开发一个新的基网络，并将其扩展以获得一系列模型，称为EfficientNets。

问题辨析(Problem Formulation)

一个卷积神经网络的层$i$可以被描述为函数$Y_i=F_i(X_i)$，其中$F_i$是卷积操作，$Y_i$是输出的张量，$X_i$ 是输入的张量且张量的形状为$<H_{\mathrm{i}},{\mathrm{W}}_{\mathrm{i}},C_{\mathrm{i}}>$，$H_i$和$W_i$是空间维度上的尺寸，$C_i$是通道维度的尺寸。一个卷积网络N可以表示为$\mathrm{N}=F_k\odot ...\odot F_2\odot F_1(X_1)={\odot }_{j=\mathrm{1...}k}{F}_j(X_1)$。实际上，卷积神经网络层通常分为多个阶段，每个阶段的所有层都具有相同的体系结构，因此将卷积神经网络定义为：
$$\mathrm{N}=\underset{i=\mathrm{1...}s}{\odot }{F}_i^{L_i}(X_{<H_{\mathrm{i}},{\mathrm{W}}_{\mathrm{i}},C_{\mathrm{i}}>})$$
其中$F_i^{L_i}$表示$F_i$架构在第$i$个阶段被重复$L_i$次，$<H_{\mathrm{i}},{\mathrm{W}}_{\mathrm{i}},C_{\mathrm{i}}>$是第$i$层输入的张量$X$形状。不同于之前常规的网络设计是集中在寻找更好的$F_i$架构，模型缩放则是扩展网络长度$L_i$，宽度$C_i$和分辨率$(H_{\mathrm{i}},{\mathrm{W}}_{\mathrm{i}})$，而不改变基网络的$F_i$。为了进一步减少设计空间的大小，限制所有参数必须以恒定的比例均匀地缩放。目标是为了在给定资源限制时最大化模型精度，可以被定义为一个优化问题：
$$\begin{array}{l}\underset{d,w,r}{\max }Accuracy\left(N\left(d,w,r\right)\right)\\ N\left(d,w,r\right)=\underset{i=\mathrm{1...}s}{\odot }\stackrel{\wedge }{F_i^{d?L_i}}\left(X_{?r?H_{\mathrm{i}},r?{\mathrm{W}}_{\mathrm{i}},w?C_{\mathrm{i}}?}\right)\\ Memory\left(N\right)\le target\_memory\\ FLOPS\left(N\right)\le target\_flops\end{array}$$
其中$w$、$d$、$r$为缩放网络宽度、深度和分辨率的系数；${\hat{F}}_i$、${\hat{H}}_i$、${\hat{W}}_i$、${\hat{C}}_i$是基础网络中预定义的参数，具体数据如下图是原论文中所示：

缩放尺寸(Scaling Dimensions)

缩放尺寸主要难点是最优的$d$、$w$、$r$相互依赖，并且在不同的资源约束下值会发生变化。由于这一困难，传统的方法大多是在其中一个维度上进行缩放。

1. Depth($d$)： 缩放网络深度是许多卷积神经网络最常用的方法，更深层次的卷积神经网络可以捕获更丰富、更复杂的特性，并很好地概括新的任务。然而由于梯度消失问题，更深层次的网络也更加难以训练。虽然有一些技术，如跳过连接和批处理标准化，缓解了训练问题，但非常深的网络的精度增益会减少。原论文下图(左)对不同深度系数$d$的基础模型进行缩放的实证研究，进一步表明对于非常深的卷积神经网络精度收益递减。
2. Width($w$)： 小型模型通常采用网络宽度缩放，更广泛的网络往往能够捕获更细粒度的特点，更容易训练。然而非常宽但很浅的网络往往难以捕获更高层次的特性。原论文下图(中)中得到的经验结果表明，当网络越宽$w$越大时，准确率会迅速饱和。
3. Resolution($r$)： 使用更高分辨率的输入图像，卷积神经网络可以捕获更细粒度的模式。早期的卷积神经网络通常使用224x224分辨率的图像，目前的卷积神经网络则使用299x299或331x331分辨率的图像来获得更好的精度。最近有网络使用480x480分辨率的图像在ImageNet上实现了最优秀的精度。更高的分辨率如600x600也广泛应用于目标检测卷积神经网络。原论文下图(右)中显示了缩放网络分辨率的结果，证明更高的分辨率可以提高精度，但是对于非常高的分辨率，精度增益会减小($r=1.0$表示分辨率224x224)。

上述分析使我们得出了第一个观察结果：增大网络宽度、深度或分辨率的任何维度都会提高精度，但对于较大的模型，精度增益会减小。

复合缩放(Compound Scaling)

根据以往经验可以得到一种假设：不同的尺度尺度并不是独立的。比如，对于高分辨率的图像应该增加网络深度，因为较大的感受野可以在较大的图像中帮助捕获包含更多像素的特征。这种假设表明，卷积神经网络网络性能的提升需要协调和平衡不同的尺度而不是传统的单一尺度。
为了验证这种假设，原论文中比较了不同网络深度和分辨率下的宽度缩放，如下图所示。如果只缩放网络宽度$w$ (蓝线) 而不改变深度($d=1.0$)和分辨率($r=1.0$)，则精度很快达到饱和。随着更深的网络和更高的分辨率，在相同的计算成本下，宽度缩放可以获得更好的精度。

上述分析使我们得出了第二个观察结果：为了追求更好的精度和效率，在卷积神经网络缩放期间平衡网络宽度、深度和分辨率的所有维度至关重要。
在论文中，我们提出了一种新的复合缩放方法，它使用复合系数$?$以理论性的方式均匀缩放网络的宽度、深度和分辨率：
$$\begin{array}{l}\mathrm{depth}:\mathrm{d}={\alpha }^{?}\\ \mathrm{width}:\mathrm{w}={\beta }^{?}\\ \mathrm{resolution}:\mathrm{r}={\gamma }^{?}\\ \alpha ?{\beta }^2?{\gamma }^2\approx 2\\ \alpha \ge 1,\beta \ge 1,\gamma \ge 1\end{array}$$
其中$\alpha$，$\beta$，$\gamma$是可以通过小网格搜索确定的常数。$?$是一个用户指定的系数，它控制着有多少资源可用于模型缩放，而$\alpha$，$\beta$，$\gamma$则分别指定如何将这些额外的资源分配给网络宽度、深度和分辨率。

常规卷积运算的浮点运算FLOPs与$d$、$w^2$、$r^2$成比例，即网络深度增加一倍将使FLOPs也增加一倍，但网络宽度或分辨率增加一倍将使FLOPs增加四倍。

由于卷积运算通常在卷积神经网络中占主导地位，用上述公式缩放卷积神经网络将使总的FLOPs增加${\left(\alpha \times {\beta }^2\times {\gamma }^2\right)}^{?}$，原论文约束$\alpha ?{\beta }^2?{\gamma }^2\approx 2$，使得对于任何一个新的$?$，总的Flops都将大约增加$2^{?}$。

EfficientNet_V1的模型结构

模型缩放不会改变基础网络中的层操作符$F_i$，因此基础网络很重要。原论文使用MnasNet的方法搜索，利用多目标神经网络架构搜索，同时优化准确率和FLOPS产生了一个高效的网络，将其命名为 EfficientNet-B0(FLOPS为400M)，下图是原论文给出的关于 EfficientNet-B0模型结构的详细示意图：

固定$\alpha$，$\beta$，$\gamma$并使用不同的$?$对基础网络进行扩展，得到了EfficientNet-B1到B7

EfficientNet_V1在图像分类中分为两部分：backbone部分： 主要由MBConv基础单元、卷积层组成，分类器部分：由卷积层、全局池化层和全连接层组成 。

神经网络架构搜索的技术路线参考：

以下内容是原论文中没有的补充内容，关于EfficientNet_V1结构的更细节描述。

SE模块(Squeeze Excitation)

对所通道输出的特征图进行加权: SE模块显式地建立特征通道之间的相互依赖关系，通过学习能够计算出每个通道的重要程度，然后依照重要程度对各个通道上的特征进行加权，从而突出重要特征，抑制不重要的特征。
SE模块的示意图如下图所示：

1. 压缩(squeeze)： 由于卷积只是在局部空间内进行操作，很难获得全局的信息发现通道之间的关系特征，因此采用全局平局池化将每个通道上的空间特征编码压缩为一个全局特征完成特征信息的进行融合。
2. 激励(excitation)： 接收每个通道的全局特征后，采用俩个全连接层预测每个通道的重要性(激励)。为了降低计算量，第一个全连接层带有缩放超参数起到减少通道、降低维度的作用；第二个全连接层则恢复原始维度，以保证通道的重要性与通道的特征图数量完全匹配。
3. 加权(scale)： 计算出通道的重要性后，下一步对通道的原始特征图进行加权操作，各通道权重分别和对应通道的原始特征图相乘获得新的加权特征图。

EfficientNet_V1中的SE模块：

反向残差结构 MBConv

ResNet【参考】中证明残差结构(Residuals) 有助于构建更深的网络从而提高精度，MobileNets_V2【参考】中以ResNet的残差结构为基础进行优化，提出了反向残差(Inverted Residuals) 的概念。
反向残差结构的过程: 低维输入->1x1点卷积(升维)-> bn层+swish激活->3x3深度卷积(低维)->bn层+swish激活->1x1点卷积(降维)->与残差相加->bn层。

EfficientNet_V1常规的反向残差结构分为俩种，当stride=2时，反向残差结构取消了shortcut连接。

EfficientNet_V1还有一个特殊的反向残差结构，它没有用于升维的1x1点卷积。

在MobileNets_V2都是使用ReLU6激活函数，但EfficientNet_V1使用现在比较常用的是swish激活函数，即x乘上sigmoid激活函数:
$$\mathrm{swish}(x)=x\sigma (x)$$
其中sigmoid激活函数：
$$\sigma (x)=\frac{1}{1+e^{?x}}$$

反向残差结构组 EnetStage

EfficientNet_V1由多个反向残差结构组构成，除了stride的细微差异，每个反向残差结构组具有相同的网络结构，以下是EfficientNet-B0模型参数以及对应的网络结构图。

---

EfficientNet_V1 Pytorch代码

卷积块： 3×3/5×5卷积层+BN层+Swish激活函数(可选)

# 卷积块:3×3/5×5卷积层+BN层+Swish激活函数(可选)
class ConvBNAct(nn.Module):
    def __init__(self,
                 out_channels,          # 输出通道
                 activation=None,       # 激活函数
                 bn_epsilon=None,       # BN层参数
                 bn_momentum=None,      # BN层参数
                 same_padding=False,    # 标识记号:自定义输入图像分辨率需要额外独立设计卷积层
                 **kwargs):
        super(ConvBNAct, self).__init__()
        # 通常反向残差结构MBConv的深度卷积需要额外独立设计卷积层
        _conv_cls = SamePaddingConv2d if same_padding else nn.Conv2d
        self.conv = _conv_cls(out_channels=out_channels, **kwargs)
        # 配置bn层
        bn_kwargs = {}
        if bn_epsilon is not None:
            bn_kwargs["eps"] = bn_epsilon
        if bn_momentum is not None:
            bn_kwargs["momentum"] = bn_momentum
        self.bn = nn.BatchNorm2d(out_channels, **bn_kwargs)
        # 配置激活函数
        self.activation = activation

    # 获得卷积块的输入分辨率
    @property
    def in_spatial_shape(self):
        if isinstance(self.conv, SamePaddingConv2d):
            return self.conv.in_spatial_shape
        else:
            return None

    # 获得卷积块的输出分辨率
    @property
    def out_spatial_shape(self):
        if isinstance(self.conv, SamePaddingConv2d):
            return self.conv.out_spatial_shape
        else:
            return None

    # 获得卷积块的输入通道数
    @property
    def in_channels(self):
        return self.conv.in_channels

    # 获得卷积块的输出通道数
    @property
    def out_channels(self):
        return self.conv.out_channels

    def forward(self, x):
        x = self.conv(x)
        x = self.bn(x)
        if self.activation is not None:
            x = self.activation(x)
        return x

额外单独设计的卷积层

# 额外单独设计的卷积层
class SamePaddingConv2d(nn.Module):
    def __init__(self,
                 in_spatial_shape,      # 输入分辨率
                 in_channels,           # 输入通道数
                 out_channels,          # 输出通道数
                 kernel_size,           # 卷积核大小
                 stride,                # 卷积核步长
                 dilation=1,            # 空洞卷积空洞值
                 enforce_in_spatial_shape=False,    # 检测标识:输入到卷积层的分辨率是否符合规定
                 **kwargs):
        super(SamePaddingConv2d, self).__init__()
        # 输入图像尺寸(w,h)
        self._in_spatial_shape = _pair(in_spatial_shape)
        # 检测标识
        self.enforce_in_spatial_shape = enforce_in_spatial_shape
        # 卷积核尺寸(w,h)
        kernel_size = _pair(kernel_size)
        # 步长(w方向和h方向)
        stride = _pair(stride)
        # 空洞(w方向和h方向)
        dilation = _pair(dilation)

        in_height, in_width = self._in_spatial_shape
        filter_height, filter_width = kernel_size
        stride_heigth, stride_width = stride
        dilation_height, dilation_width = dilation

        # 计算出原始输入特征进过下采样后的输出尺寸
        # 有小数则向上取整
        out_height = int(ceil(float(in_height) / float(stride_heigth)))
        out_width = int(ceil(float(in_width) / float(stride_width)))

        # 需要padding去补满足既然向上取整的条件
        # 空洞卷积输出特征图大小的公式:o=[i+2p-k-(k-1)*(d-1)]/s +1
        # 2p=(o-1)s+k+(k-1)*(d-1)-i
        pad_along_height = max((out_height - 1) * stride_heigth +
                               filter_height + (filter_height - 1) * (dilation_height - 1) - in_height, 0)
        pad_along_width = max((out_width - 1) * stride_width +
                              filter_width + (filter_width - 1) * (dilation_width - 1) - in_width, 0)

        # 分别计算出卷积块上下左右的padding值
        pad_top = pad_along_height // 2
        pad_bottom = pad_along_height - pad_top
        pad_left = pad_along_width // 2
        pad_right = pad_along_width - pad_left
        paddings = (pad_left, pad_right, pad_top, pad_bottom)
        if any(p > 0 for p in paddings):
            self.zero_pad = nn.ZeroPad2d(paddings)
        else:
            self.zero_pad = None

        self.conv = nn.Conv2d(in_channels=in_channels,
                              out_channels=out_channels,
                              kernel_size=kernel_size,
                              stride=stride,
                              dilation=dilation,
                              **kwargs)
        # 输出分辨率
        self._out_spatial_shape = (out_height, out_width)

    # 获得卷积层的输入分辨率
    @property
    def in_spatial_shape(self):
        return self._in_spatial_shape

    # 获得卷积层的输出分辨率
    @property
    def out_spatial_shape(self):
        return self._out_spatial_shape

    # 获得卷积层的输入通道数
    @property
    def in_channels(self):
        return self.conv.in_channels

    # 获得卷积层的输出通道数
    @property
    def out_channels(self):
        return self.conv.out_channels

    # 查看输入分辨率是否符合要求
    def check_spatial_shape(self, x):
        if x.size(2) != self.in_spatial_shape[0] or \
                x.size(3) != self.in_spatial_shape[1]:
            raise ValueError(
                "Expected input spatial shape {}, got {} instead".format(self.in_spatial_shape,
                                                                         x.shape[2:]))
    def forward(self, x):
        if self.enforce_in_spatial_shape:
            self.check_spatial_shape(x)
        if self.zero_pad is not None:
            x = self.zero_pad(x)
        x = self.conv(x)
        return x

格式转换: 保证输出数据是元祖格式

# 格式转换:保证输出数据是元祖格式
def _pair(x):
    # 用于检查对象x是否是例如列表、元组、字典和字符串等container_abcs.Iterable类的实例
    # 就是要可以迭代
    if isinstance(x, container_abcs.Iterable):
        return x
    return (x, x)

SE注意力模块：： 全局平均池化+1×1卷积+Swish激活函数+1×1卷积+sigmoid激活函数

# SE注意力模块:对各通道的特征分别强化
class SqueezeExcitate(nn.Module):
    def __init__(self,
                 in_channels,       # 输入通道数
                 se_size,           # se模块降维通道数
                 activation=None):  # 激活函数
        super(SqueezeExcitate, self).__init__()
        # 1×1降维卷积
        self.dim_reduce = nn.Conv2d(in_channels=in_channels,
                                    out_channels=se_size,
                                    kernel_size=1)
        # 全连接层:1×1卷积
        self.dim_restore = nn.Conv2d(in_channels=se_size,
                                     out_channels=in_channels,
                                     kernel_size=1)
        # 激活函数
        self.activation = F.relu if activation is None else activation

    def forward(self, x):
        x = F.adaptive_avg_pool2d(x, (1, 1))
        x = self.dim_reduce(x)
        x = self.activation(x)
        x = self.dim_restore(x)
        x = torch.sigmoid(x)
        return x

反向残差结构： 1×1点卷积层+BN层+Swish激活函数+3×3深度卷积层+BN层+Swish激活函数+1×1点卷积层+BN层

# 反残差结构:1×1点卷积层+BN层+Swish激活函数+3×3深度卷积层+BN层+Swish激活函数+1×1点卷积层+BN层
class MBConvBlock(nn.Module):
    def __init__(self,
                 in_spatial_shape,          # 图片形状,元祖(height,width)或者整形int
                 in_channels,               # 输入通道数
                 out_channels,              # 输出通道数
                 kernel_size,               # 深度卷积的卷积核尺寸
                 stride,                    # 深度卷积的步长
                 expansion_factor,          # 膨胀系数
                 activation,                # 激活函数
                 bn_epsilon=None,           # BN层参数
                 bn_momentum=None,          # BN层参数
                 se_size=None,              # se注意力模块通道数
                 drop_connect_rate=None,    # 反残差结构随机失活概率
                 bias=False):               # 卷积层偏置
        super(MBConvBlock, self).__init__()
        # 通胀通道数 = 输入通道*膨胀系数 用于1×1卷积升维
        exp_channels = in_channels * expansion_factor
        # 深度卷积卷积核尺寸(元祖形式)
        kernel_size = _pair(kernel_size)
        # 深度卷积卷积核步长(元祖形式)
        stride = _pair(stride)
        self.activation = activation
        # 1×1膨胀卷积 升维
        if expansion_factor != 1:
            self.expand_conv = ConvBNAct(in_channels=in_channels,
                                         out_channels=exp_channels,
                                         kernel_size=(1, 1),
                                         bias=bias,
                                         activation=self.activation,
                                         bn_epsilon=bn_epsilon,
                                         bn_momentum=bn_momentum)
        else:
            self.expand_conv = None

        # 3×3或5×5深度卷积
        self.dp_conv = ConvBNAct(in_spatial_shape=in_spatial_shape,
                                 in_channels=exp_channels,
                                 out_channels=exp_channels,
                                 kernel_size=kernel_size,
                                 stride=stride,
                                 groups=exp_channels,
                                 bias=bias,
                                 activation=self.activation,
                                 same_padding=True,
                                 bn_epsilon=bn_epsilon,
                                 bn_momentum=bn_momentum)

        # se注意力模块
        if se_size is not None:
            self.se = SqueezeExcitate(exp_channels,
                                      se_size,
                                      activation=self.activation)
        else:
            self.se = None

        # 反残差结构随机失活概率
        if drop_connect_rate is not None:
            self.drop_connect = DropConnect(drop_connect_rate)
        else:
            self.drop_connect = None

        # 深度卷积步长为2则没有捷径连接
        if in_channels == out_channels and all(s == 1 for s in stride):
            self.skip_enabled = True
        else:
            self.skip_enabled = False

        # 1×1点卷积
        self.project_conv = ConvBNAct(in_channels=exp_channels,
                                      out_channels=out_channels,
                                      kernel_size=(1, 1),
                                      bias=bias,
                                      activation=None,
                                      bn_epsilon=bn_epsilon,
                                      bn_momentum=bn_momentum)
    # 获得反残差结构的输入分辨率
    @property
    def in_spatial_shape(self):
        return self.dp_conv.in_spatial_shape

    # 获得反残差结构的输出分辨率
    @property
    def out_spatial_shape(self):
        return self.dp_conv.out_spatial_shape

    # 获得反残差结构的输入分通道数
    @property
    def in_channels(self):
        if self.expand_conv is not None:
            return self.expand_conv.in_channels
        else:
            return self.dp_conv.in_channels

    # 获得反残差结构的输出分通道数
    @property
    def out_channels(self):
        return self.project_conv.out_channels

    def forward(self, x):
        inp = x
        if self.expand_conv is not None:
            # 膨胀卷积
            x = self.expand_conv(x)

        # 深度卷积
        x = self.dp_conv(x)

        # se注意力模块
        if self.se is not None:
            x = self.se(x)*x

        # 点卷积
        x = self.project_conv(x)

        if self.skip_enabled:
            # 反残差结构随机失活
            if self.drop_connect is not None:
                x = self.drop_connect(x)
            x = x + inp
        return x

反残差结构随机失活

# 反残差结构随机失活:batchsize个样本随机失活,应用于反残差结构的主路径
class DropConnect(nn.Module):
    def __init__(self, rate=0.5):
        super(DropConnect, self).__init__()
        self.keep_prob = None
        self.set_rate(rate)

    # 反残差结构的保留率
    def set_rate(self, rate):
        if not 0 <= rate < 1:
            raise ValueError("rate must be 0<=rate<1, got {} instead".format(rate))
        self.keep_prob = 1 - rate

    def forward(self, x):
        # 训练阶段随机丢失特征
        if self.training:
            # 是否保留取决于固定保留概率+随机概率
            random_tensor = self.keep_prob + torch.rand([x.size(0), 1, 1, 1],
                                                        dtype=x.dtype,
                                                        device=x.device)
            # 0表示丢失 1表示保留
            binary_tensor = torch.floor(random_tensor)
            # self.keep_prob个人理解对保留特征进行强化,概率越低强化越明显
            return torch.mul(torch.div(x, self.keep_prob), binary_tensor)
        else:
            return x

---

完整代码

from math import ceil
import torch
import torch.nn as nn
import torch.nn.functional as F
import collections.abc as container_abcs
from torch.utils import model_zoo
from torchsummary import summary

# 格式转换:保证输出数据是元祖格式
def _pair(x):
    # 用于检查对象x是否是例如列表、元组、字典和字符串等container_abcs.Iterable类的实例
    # 就是要可以迭代
    if isinstance(x, container_abcs.Iterable):
        return x
    return (x, x)

# 额外单独设计的卷积层
class SamePaddingConv2d(nn.Module):
    def __init__(self,
                 in_spatial_shape,      # 输入分辨率
                 in_channels,           # 输入通道数
                 out_channels,          # 输出通道数
                 kernel_size,           # 卷积核大小
                 stride,                # 卷积核步长
                 dilation=1,            # 空洞卷积空洞值
                 enforce_in_spatial_shape=False,    # 检测标识:输入到卷积层的分辨率是否符合规定
                 **kwargs):
        super(SamePaddingConv2d, self).__init__()
        # 输入图像尺寸(w,h)
        self._in_spatial_shape = _pair(in_spatial_shape)
        # 检测标识
        self.enforce_in_spatial_shape = enforce_in_spatial_shape
        # 卷积核尺寸(w,h)
        kernel_size = _pair(kernel_size)
        # 步长(w方向和h方向)
        stride = _pair(stride)
        # 空洞(w方向和h方向)
        dilation = _pair(dilation)

        in_height, in_width = self._in_spatial_shape
        filter_height, filter_width = kernel_size
        stride_heigth, stride_width = stride
        dilation_height, dilation_width = dilation

        # 计算出原始输入特征进过下采样后的输出尺寸
        # 有小数则向上取整
        out_height = int(ceil(float(in_height) / float(stride_heigth)))
        out_width = int(ceil(float(in_width) / float(stride_width)))

        # 需要padding去补满足既然向上取整的条件
        # 空洞卷积输出特征图大小的公式:o=[i+2p-k-(k-1)*(d-1)]/s +1
        # 2p=(o-1)s+k+(k-1)*(d-1)-i
        pad_along_height = max((out_height - 1) * stride_heigth +
                               filter_height + (filter_height - 1) * (dilation_height - 1) - in_height, 0)
        pad_along_width = max((out_width - 1) * stride_width +
                              filter_width + (filter_width - 1) * (dilation_width - 1) - in_width, 0)

        # 分别计算出卷积块上下左右的padding值
        pad_top = pad_along_height // 2
        pad_bottom = pad_along_height - pad_top
        pad_left = pad_along_width // 2
        pad_right = pad_along_width - pad_left
        paddings = (pad_left, pad_right, pad_top, pad_bottom)
        if any(p > 0 for p in paddings):
            self.zero_pad = nn.ZeroPad2d(paddings)
        else:
            self.zero_pad = None

        self.conv = nn.Conv2d(in_channels=in_channels,
                              out_channels=out_channels,
                              kernel_size=kernel_size,
                              stride=stride,
                              dilation=dilation,
                              **kwargs)
        # 输出分辨率
        self._out_spatial_shape = (out_height, out_width)

    # 获得卷积层的输入分辨率
    @property
    def in_spatial_shape(self):
        return self._in_spatial_shape

    # 获得卷积层的输出分辨率
    @property
    def out_spatial_shape(self):
        return self._out_spatial_shape

    # 获得卷积层的输入通道数
    @property
    def in_channels(self):
        return self.conv.in_channels

    # 获得卷积层的输出通道数
    @property
    def out_channels(self):
        return self.conv.out_channels

    # 查看输入分辨率是否符合要求
    def check_spatial_shape(self, x):
        if x.size(2) != self.in_spatial_shape[0] or \
                x.size(3) != self.in_spatial_shape[1]:
            raise ValueError(
                "Expected input spatial shape {}, got {} instead".format(self.in_spatial_shape,
                                                                         x.shape[2:]))
    def forward(self, x):
        if self.enforce_in_spatial_shape:
            self.check_spatial_shape(x)
        if self.zero_pad is not None:
            x = self.zero_pad(x)
        x = self.conv(x)
        return x

# 卷积块:3×3/5×5卷积层+BN层+Swish激活函数(可选)
class ConvBNAct(nn.Module):
    def __init__(self,
                 out_channels,          # 输出通道
                 activation=None,       # 激活函数
                 bn_epsilon=None,       # BN层参数
                 bn_momentum=None,      # BN层参数
                 same_padding=False,    # 标识记号:自定义输入图像分辨率需要额外独立设计卷积层
                 **kwargs):
        super(ConvBNAct, self).__init__()
        # 通常反向残差结构MBConv的深度卷积需要额外独立设计卷积层
        _conv_cls = SamePaddingConv2d if same_padding else nn.Conv2d
        self.conv = _conv_cls(out_channels=out_channels, **kwargs)
        # 配置bn层
        bn_kwargs = {}
        if bn_epsilon is not None:
            bn_kwargs["eps"] = bn_epsilon
        if bn_momentum is not None:
            bn_kwargs["momentum"] = bn_momentum
        self.bn = nn.BatchNorm2d(out_channels, **bn_kwargs)
        # 配置激活函数
        self.activation = activation

    # 获得卷积块的输入分辨率
    @property
    def in_spatial_shape(self):
        if isinstance(self.conv, SamePaddingConv2d):
            return self.conv.in_spatial_shape
        else:
            return None

    # 获得卷积块的输出分辨率
    @property
    def out_spatial_shape(self):
        if isinstance(self.conv, SamePaddingConv2d):
            return self.conv.out_spatial_shape
        else:
            return None

    # 获得卷积块的输入通道数
    @property
    def in_channels(self):
        return self.conv.in_channels

    # 获得卷积块的输出通道数
    @property
    def out_channels(self):
        return self.conv.out_channels

    def forward(self, x):
        x = self.conv(x)
        x = self.bn(x)
        if self.activation is not None:
            x = self.activation(x)
        return x

# 激活函数
class Swish(nn.Module):
    def __init__(self,
                 beta=1.0,
                 beta_learnable=False):
        super(Swish, self).__init__()

        if beta == 1.0 and not beta_learnable:
            self._op = self.simple_swish
        else:
            self.beta = nn.Parameter(torch.full([1], beta),
                                     requires_grad=beta_learnable)
            self._op = self.advanced_swish

    # 俩种不同的激活模式,一种多了权重系数beta
    # 常规Swish
    def simple_swish(self, x):
        # x * torch.sigmoid(x) 等价于 nn.SiLU()
        return x * torch.sigmoid(x)
    # 加权Swish
    def advanced_swish(self, x):
        return x * torch.sigmoid(self.beta * x)

    def forward(self, x):
        return self._op(x)

# 反残差结构随机失活:batchsize个样本随机失活,应用于反残差结构的主路径
class DropConnect(nn.Module):
    def __init__(self, rate=0.5):
        super(DropConnect, self).__init__()
        self.keep_prob = None
        self.set_rate(rate)

    # 反残差结构的保留率
    def set_rate(self, rate):
        if not 0 <= rate < 1:
            raise ValueError("rate must be 0<=rate<1, got {} instead".format(rate))
        self.keep_prob = 1 - rate

    def forward(self, x):
        # 训练阶段随机丢失特征
        if self.training:
            # 是否保留取决于固定保留概率+随机概率
            random_tensor = self.keep_prob + torch.rand([x.size(0), 1, 1, 1],
                                                        dtype=x.dtype,
                                                        device=x.device)
            # 0表示丢失 1表示保留
            binary_tensor = torch.floor(random_tensor)
            # self.keep_prob个人理解对保留特征进行强化,概率越低强化越明显
            return torch.mul(torch.div(x, self.keep_prob), binary_tensor)
        else:
            return x

# SE注意力模块:对各通道的特征分别强化
class SqueezeExcitate(nn.Module):
    def __init__(self,
                 in_channels,       # 输入通道数
                 se_size,           # se模块降维通道数
                 activation=None):  # 激活函数
        super(SqueezeExcitate, self).__init__()
        # 1×1降维卷积
        self.dim_reduce = nn.Conv2d(in_channels=in_channels,
                                    out_channels=se_size,
                                    kernel_size=1)
        # 全连接层:1×1卷积
        self.dim_restore = nn.Conv2d(in_channels=se_size,
                                     out_channels=in_channels,
                                     kernel_size=1)
        # 激活函数
        self.activation = F.relu if activation is None else activation

    def forward(self, x):
        x = F.adaptive_avg_pool2d(x, (1, 1))
        x = self.dim_reduce(x)
        x = self.activation(x)
        x = self.dim_restore(x)
        x = torch.sigmoid(x)
        return x

# 反残差结构:1×1点卷积层+BN层+Swish激活函数+3×3深度卷积层+BN层+Swish激活函数+1×1点卷积层+BN层
class MBConvBlock(nn.Module):
    def __init__(self,
                 in_spatial_shape,          # 图片形状,元祖(height,width)或者整形int
                 in_channels,               # 输入通道数
                 out_channels,              # 输出通道数
                 kernel_size,               # 深度卷积的卷积核尺寸
                 stride,                    # 深度卷积的步长
                 expansion_factor,          # 膨胀系数
                 activation,                # 激活函数
                 bn_epsilon=None,           # BN层参数
                 bn_momentum=None,          # BN层参数
                 se_size=None,              # se注意力模块通道数
                 drop_connect_rate=None,    # 反残差结构随机失活概率
                 bias=False):               # 卷积层偏置
        super(MBConvBlock, self).__init__()
        # 通胀通道数 = 输入通道*膨胀系数 用于1×1卷积升维
        exp_channels = in_channels * expansion_factor
        # 深度卷积卷积核尺寸(元祖形式)
        kernel_size = _pair(kernel_size)
        # 深度卷积卷积核步长(元祖形式)
        stride = _pair(stride)
        self.activation = activation
        # 1×1膨胀卷积 升维
        if expansion_factor != 1:
            self.expand_conv = ConvBNAct(in_channels=in_channels,
                                         out_channels=exp_channels,
                                         kernel_size=(1, 1),
                                         bias=bias,
                                         activation=self.activation,
                                         bn_epsilon=bn_epsilon,
                                         bn_momentum=bn_momentum)
        else:
            self.expand_conv = None

        # 3×3或5×5深度卷积
        self.dp_conv = ConvBNAct(in_spatial_shape=in_spatial_shape,
                                 in_channels=exp_channels,
                                 out_channels=exp_channels,
                                 kernel_size=kernel_size,
                                 stride=stride,
                                 groups=exp_channels,
                                 bias=bias,
                                 activation=self.activation,
                                 same_padding=True,
                                 bn_epsilon=bn_epsilon,
                                 bn_momentum=bn_momentum)

        # se注意力模块
        if se_size is not None:
            self.se = SqueezeExcitate(exp_channels,
                                      se_size,
                                      activation=self.activation)
        else:
            self.se = None

        # 反残差结构随机失活概率
        if drop_connect_rate is not None:
            self.drop_connect = DropConnect(drop_connect_rate)
        else:
            self.drop_connect = None

        # 深度卷积步长为2则没有捷径连接
        if in_channels == out_channels and all(s == 1 for s in stride):
            self.skip_enabled = True
        else:
            self.skip_enabled = False

        # 1×1点卷积
        self.project_conv = ConvBNAct(in_channels=exp_channels,
                                      out_channels=out_channels,
                                      kernel_size=(1, 1),
                                      bias=bias,
                                      activation=None,
                                      bn_epsilon=bn_epsilon,
                                      bn_momentum=bn_momentum)
    # 获得反残差结构的输入分辨率
    @property
    def in_spatial_shape(self):
        return self.dp_conv.in_spatial_shape

    # 获得反残差结构的输出分辨率
    @property
    def out_spatial_shape(self):
        return self.dp_conv.out_spatial_shape

    # 获得反残差结构的输入分通道数
    @property
    def in_channels(self):
        if self.expand_conv is not None:
            return self.expand_conv.in_channels
        else:
            return self.dp_conv.in_channels

    # 获得反残差结构的输出分通道数
    @property
    def out_channels(self):
        return self.project_conv.out_channels

    def forward(self, x):
        inp = x
        if self.expand_conv is not None:
            # 膨胀卷积
            x = self.expand_conv(x)

        # 深度卷积
        x = self.dp_conv(x)

        # se注意力模块
        if self.se is not None:
            x = self.se(x)*x

        # 点卷积
        x = self.project_conv(x)

        if self.skip_enabled:
            # 反残差结构随机失活
            if self.drop_connect is not None:
                x = self.drop_connect(x)
            x = x + inp
        return x

# 反残差结构组
class EnetStage(nn.Module):
    def __init__(self,
                 num_layers,            # 反残差结构个数
                 in_spatial_shape,      # 输入分辨率
                 in_channels,           # 输入通道数
                 out_channels,          # 输出通道数
                 stride,                # 卷积核步长
                 se_ratio,              # 用于se注意力模块降维
                 drop_connect_rates,    # 反残差结构随机失活概率
                 **kwargs):
        super(EnetStage, self).__init__()

        # 反残差结构个数
        self.num_layers = num_layers
        self.layers = nn.ModuleList()
        # 输入分辨率
        spatial_shape = in_spatial_shape
        for i in range(self.num_layers):
            # 计算se模块的降维后的通道数
            se_size = max(1, in_channels // se_ratio)
            # 反残差结构
            layer = MBConvBlock(in_spatial_shape=spatial_shape,
                                in_channels=in_channels,
                                out_channels=out_channels,
                                stride=stride,
                                se_size=se_size,
                                drop_connect_rate=drop_connect_rates[i],
                                **kwargs)
            self.layers.append(layer)
            # 新的输入分辨率
            spatial_shape = layer.out_spatial_shape
            # 新步长
            stride = 1
            # 新的输入通道数
            in_channels = out_channels

    # 获得反残差结构组的输入分辨率
    @property
    def in_spatial_shape(self):
        return self.layers[0].in_spatial_shape

    # 获得反残差结构组的输出分辨率
    @property
    def out_spatial_shape(self):
        return self.layers[-1].out_spatial_shape

    # 获得反残差结构组的输入通道数
    @property
    def in_channels(self):
        return self.layers[0].in_channels

    # 获得反残差结构组的输出通道数
    @property
    def out_channels(self):
        return self.layers[-1].out_channels

    def forward(self, x):
        for layer in self.layers:
            x = layer(x)
        return x

def _make_divisible(filters, width_coefficient, depth_divisor=8, min_depth=None):
    '''
    int(filters + depth_divisor / 2) // depth_divisor * depth_divisor)
    目的是为了让new_filters是depth_divisor的整数倍
    类似于四舍五入:filters超过depth_divisor的一半则加1保留;不满一半则归零舍弃
    '''
    if min_depth is None:
        min_depth = depth_divisor
    filters *= width_coefficient
    new_filters = max(min_depth, int(filters + depth_divisor / 2) // depth_divisor * depth_divisor)
    # 确保下降幅度不超过10%
    if new_filters < 0.9 * filters:
        new_filters += depth_divisor
    return int(new_filters)

# 保证计算值是整数
def round_repeats(repeats, depth_coefficient):
    return int(ceil(depth_coefficient * repeats))


class EfficientNet(nn.Module):
    # 根据基础网络缩放配置出多个网络
    # 宽度缩放 深度缩放 通道随机失活率 输入图像分辨率
    # (width_coefficient, depth_coefficient, dropout_rate, in_spatial_shape)
    coefficients = [
        (1.0, 1.0, 0.2, 224),
        (1.0, 1.1, 0.2, 240),
        (1.1, 1.2, 0.3, 260),
        (1.2, 1.4, 0.3, 300),
        (1.4, 1.8, 0.4, 380),
        (1.6, 2.2, 0.4, 456),
        (1.8, 2.6, 0.5, 528),
        (2.0, 3.1, 0.5, 600),
    ]

    # 基础网络的网络配置
    # 反残差结构 重复次数 卷积核大小 卷积核步长 膨胀系数 输入通道数 输出通道数 se模块压缩率
    # block_repeat, kernel_size, stride, expansion_factor, input_channels, output_channels, se_ratio
    stage_args = [
        [1, 3, 1, 1, 32, 16, 4],
        [2, 3, 2, 6, 16, 24, 4],
        [2, 5, 2, 6, 24, 40, 4],
        [3, 3, 2, 6, 40, 80, 4],
        [3, 5, 1, 6, 80, 112, 4],
        [4, 5, 2, 6, 112, 192, 4],
        [1, 3, 1, 6, 192, 320, 4],
    ]

    # 权重的下载地址
    state_dict_urls = [
        "https://api.onedrive.com/v1.0/shares/u!aHR0cHM6Ly8xZHJ2Lm1zL3UvcyFBdGlRcHc5VGNjZmliYV9HaE5PWWVEbXVMd3c/root/content",
        "https://api.onedrive.com/v1.0/shares/u!aHR0cHM6Ly8xZHJ2Lm1zL3UvcyFBdGlRcHc5VGNjZmlicV9HaE5PWWVEbXVMd3c/root/content",
        "https://api.onedrive.com/v1.0/shares/u!aHR0cHM6Ly8xZHJ2Lm1zL3UvcyFBdGlRcHc5VGNjZmliNl9HaE5PWWVEbXVMd3c/root/content",
        "https://api.onedrive.com/v1.0/shares/u!aHR0cHM6Ly8xZHJ2Lm1zL3UvcyFBdGlRcHc5VGNjZmljS19HaE5PWWVEbXVMd3c/root/content",
        "https://api.onedrive.com/v1.0/shares/u!aHR0cHM6Ly8xZHJ2Lm1zL3UvcyFBdGlRcHc5VGNjZmljYV9HaE5PWWVEbXVMd3c/root/content",
        "https://api.onedrive.com/v1.0/shares/u!aHR0cHM6Ly8xZHJ2Lm1zL3UvcyFBdGlRcHc5VGNjZmljcV9HaE5PWWVEbXVMd3c/root/content",
        "https://api.onedrive.com/v1.0/shares/u!aHR0cHM6Ly8xZHJ2Lm1zL3UvcyFBdGlRcHc5VGNjZmljNl9HaE5PWWVEbXVMd3c/root/content",
        "https://api.onedrive.com/v1.0/shares/u!aHR0cHM6Ly8xZHJ2Lm1zL3UvcyFBdGlRcHc5VGNjZmlkS19HaE5PWWVEbXVMd3c/root/content",
    ]
    # 对应网络的权重名字
    dict_names = [
        'efficientnet-b0-d86f8792.pth',
        'efficientnet-b1-82896633.pth',
        'efficientnet-b2-e4b93854.pth',
        'efficientnet-b3-3b9ca610.pth',
        'efficientnet-b4-24436ca5.pth',
        'efficientnet-b5-d8e577e8.pth',
        'efficientnet-b6-f20845c7.pth',
        'efficientnet-b7-86e8e374.pth'
    ]

    def __init__(self,
                 b,                             # 模型序号
                 in_channels=3,                 # 输入通道
                 n_classes=1000,                # 输出通道
                 in_spatial_shape=None,         # 输入图像分辨率
                 activation=Swish(),            # 激活函数
                 bias=False,                    # 卷积网络偏置
                 drop_connect_rate=0.2,         # 反残差结构随机失活概率
                 dropout_rate=None,             # 通道随机失活率
                 bn_epsilon=1e-3,               # bn层参数
                 bn_momentum=0.01,              # bn层参数
                 pretrained=False,              # 是否加载预训练权重
                 progress=False):               # 显示下载预训练权重进度条
        super(EfficientNet, self).__init__()
        # 模型序号 0 代表牌 EfficientNet-B0
        self.b = b
        # 输入通道
        self.in_channels = in_channels
        #  激活函数
        self.activation = activation
        # 反残差结构随机失活概率
        self.drop_connect_rate = drop_connect_rate
        # 通道随机失活率
        self._override_dropout_rate = dropout_rate

        width_coefficient, _, _, spatial_shape = EfficientNet.coefficients[self.b]

        if in_spatial_shape is not None:
            self.in_spatial_shape = _pair(in_spatial_shape)
        else:
            self.in_spatial_shape = _pair(spatial_shape)

        # 初始化卷积数
        init_conv_out_channels = _make_divisible(32, width_coefficient)
        # 第一次层3×3卷积层
        self.init_conv = ConvBNAct(in_spatial_shape=self.in_spatial_shape,
                                   in_channels=self.in_channels,
                                   out_channels=init_conv_out_channels,
                                   kernel_size=(3, 3),
                                   stride=(2, 2),
                                   bias=bias,
                                   activation=self.activation,
                                   same_padding=True,
                                   bn_epsilon=bn_epsilon,
                                   bn_momentum=bn_momentum)
        # 因为输入的特征图shape不再统一,因此需要单独获取输出特征图的shape
        spatial_shape = self.init_conv.out_spatial_shape

        self.stages = nn.ModuleList()
        # 反残差结构组首个反残差结构序号
        mbconv_idx = 0
        # 当前模型所有反残差结构的随机失活概率
        dc_rates = self.get_dc_rates()
        # 根据反残差结构组组数配置不同组的参数
        for stage_id in range(self.num_stages):
            # 当前组的卷积核大小
            kernel_size = self.get_stage_kernel_size(stage_id)
            # 当前组的卷积核步长
            stride = self.get_stage_stride(stage_id)
            # 当前组的膨胀系数
            expansion_factor = self.get_stage_expansion_factor(stage_id)
            # 当前组的输入通道数
            stage_in_channels = self.get_stage_in_channels(stage_id)
            # 当前组的输出通道数
            stage_out_channels = self.get_stage_out_channels(stage_id)
            # 当前组的反残差结构个数(深度)
            stage_num_layers = self.get_stage_num_layers(stage_id)
            # 当前组的每个反残差结构的随机失活概率
            stage_dc_rates = dc_rates[mbconv_idx:mbconv_idx + stage_num_layers]
            # 当前组的se模块压缩率
            stage_se_ratio = self.get_stage_se_ratio(stage_id)
            # 构建当前反残差结构组
            stage = EnetStage(num_layers=stage_num_layers,
                              in_spatial_shape=spatial_shape,
                              in_channels=stage_in_channels,
                              out_channels=stage_out_channels,
                              stride=stride,
                              se_ratio=stage_se_ratio,
                              drop_connect_rates=stage_dc_rates,
                              kernel_size=kernel_size,
                              expansion_factor=expansion_factor,
                              activation=self.activation,
                              bn_epsilon=bn_epsilon,
                              bn_momentum=bn_momentum,
                              bias=bias
                              )
            self.stages.append(stage)
            spatial_shape = stage.out_spatial_shape
            mbconv_idx += stage_num_layers

        head_conv_out_channels = _make_divisible(1280, width_coefficient)
        head_conv_in_channels = self.stages[-1].layers[-1].project_conv.out_channels

        self.head_conv = ConvBNAct(in_channels=head_conv_in_channels,
                                   out_channels=head_conv_out_channels,
                                   kernel_size=(1, 1),
                                   bias=bias,
                                   activation=self.activation,
                                   bn_epsilon=bn_epsilon,
                                   bn_momentum=bn_momentum)
        # 全连接层通道随机失活
        if self.dropout_rate > 0:
            self.dropout = nn.Dropout(p=self.dropout_rate)
        else:
            self.dropout = None
        # 全局平均池化
        self.avpool = nn.AdaptiveAvgPool2d((1, 1))
        # 输出
        self.fc = nn.Linear(head_conv_out_channels, n_classes)

        # 加载预训练权重
        if pretrained:
            self._load_state(self.b, in_channels, n_classes, progress)

    # 模型的反残差结构组组数
    @property
    def num_stages(self):
        return len(EfficientNet.stage_args)

    # 当前模型的宽度缩放
    @property
    def width_coefficient(self):
        return EfficientNet.coefficients[self.b][0]

    # 当前模型的深度缩放
    @property
    def depth_coefficient(self):
        return EfficientNet.coefficients[self.b][1]

    # 当前模型的通道随机失活率(自定义或默认)
    @property
    def dropout_rate(self):
        # 默认
        if self._override_dropout_rate is None:
            return EfficientNet.coefficients[self.b][2]
        # 自定义
        else:
            return self._override_dropout_rate

    # 当前组的卷积核大小
    def get_stage_kernel_size(self, stage):
        return EfficientNet.stage_args[stage][1]

    # 当前组的卷积核步长
    def get_stage_stride(self, stage):
        return EfficientNet.stage_args[stage][2]

    # 当前组的膨胀系数
    def get_stage_expansion_factor(self, stage):
        return EfficientNet.stage_args[stage][3]

    # 当前组的输入通道数
    def get_stage_in_channels(self, stage):
        width_coefficient = self.width_coefficient
        in_channels = EfficientNet.stage_args[stage][4]
        return _make_divisible(in_channels, width_coefficient)

    # 当前组的输出通道数
    def get_stage_out_channels(self, stage):
        width_coefficient = self.width_coefficient
        out_channels = EfficientNet.stage_args[stage][5]
        return _make_divisible(out_channels, width_coefficient)

    # 当前组的se模块压缩率(降维)
    def get_stage_se_ratio(self, stage):
        return EfficientNet.stage_args[stage][6]

    # 当前模型的某个反残差结构组的深度
    def get_stage_num_layers(self, stage):
        depth_coefficient = self.depth_coefficient
        # 基础网络的某个反残差结构组的深度(组数)
        num_layers = EfficientNet.stage_args[stage][0]
        # 当前模型的某个反残差结构组的深度=基础网络的某个反残差结构组的深度×深度缩放
        return round_repeats(num_layers, depth_coefficient)

    # 当前模型的所有反残差结构组的深度
    def get_num_mbconv_layers(self):
        total = 0
        for i in range(self.num_stages):
            total += self.get_stage_num_layers(i)
        return total

    # 当前模型的所有反残差结构组的随机失活概率
    def get_dc_rates(self):
        total_mbconv_layers = self.get_num_mbconv_layers()
        # 反残差结构随机失活概率随着网络深度递增,范围在[0,drop_connect_rate)
        return [self.drop_connect_rate * i / total_mbconv_layers
                for i in range(total_mbconv_layers)]

    # 权重下载加载
    def _load_state(self, b, in_channels, n_classes, progress):
        state_dict = model_zoo.load_url(EfficientNet.state_dict_urls[b], progress=progress, file_name=EfficientNet.dict_names[b])
        strict = True
        # 输入通道不是3并且输出通道不是1000就不加载预训练模型
        if in_channels != 3:
            state_dict.pop('init_conv.conv.conv.weight')
            strict = False
        if n_classes != 1000:
            state_dict.pop('fc.weight')
            state_dict.pop('fc.bias')
            strict = False
        self.load_state_dict(state_dict, strict=strict)
        print("Model weights loaded successfully.")

    # 检查输入的图像是否合规
    def check_input(self, x):
        if x.dim() != 4:
            raise ValueError("Input x must be 4 dimensional tensor, got {} instead".format(x.dim()))
        if x.size(1) != self.in_channels:
            raise ValueError("Input must have {} channels, got {} instead".format(self.in_channels,
                                                                                  x.size(1)))
    # 主干网络的特征
    def get_features(self, x):
        self.check_input(x)
        x = self.init_conv(x)
        # 保留每个反残差结构层的输出特征
        out = []
        for stage in self.stages:
            x = stage(x)
            out.append(x)
        return out

    def forward(self, x):
        # 只获取最后一个反残差结构的输出特征
        x = self.get_features(x)[-1]
        x = self.head_conv(x)
        x = self.avpool(x)
        x = torch.flatten(x, 1)
        if self.dropout is not None:
            x = self.dropout(x)
        x = self.fc(x)
        return x

if __name__ == '__main__':
    device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
    # EfficientNet-B1的模型结构
    model = EfficientNet(1).to(device)
    summary(model, input_size=(3, 224, 224))

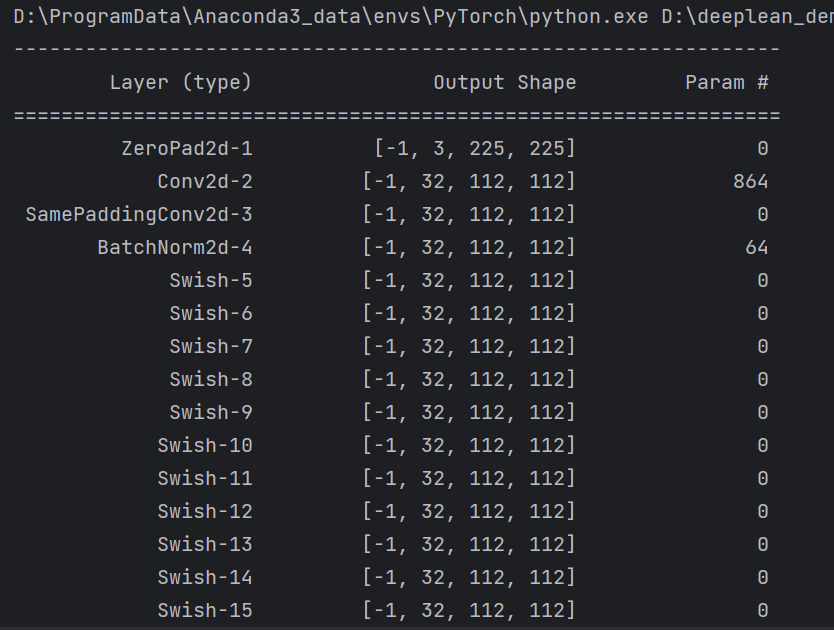
summary可以打印网络结构和参数，方便查看搭建好的网络结构。

---

总结

尽可能简单、详细的介绍了复合缩放的原理和过程，讲解了EfficientNet_V1模型的结构和pytorch代码。