算法：岛屿的周长

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

目录

一、问题描述

二、规律总结

总结

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、问题描述

给定一个包含 0 和 1 的二维网格地图，其中 1 表示陆地?0 表示水域。

岛屿中没有“湖”（“湖” 指水域在岛屿内部且不和岛屿周围的水相连）。格子是边长为 1 的正方形。网格为长方形，且宽度和高度均不超过 100 。计算这个岛屿的周长。

输入:
[[0,1,0,0],
?[1,1,1,0],
?[0,1,0,0],
?[1,1,0,0]]
输出: 16

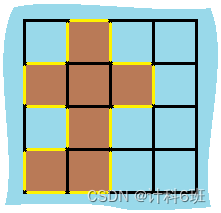
二、规律总结

解题思路：

这个题很典型的有规律，我们看上图，可以看到每个黄色的格子有四个边，周长为4，如果两个格子挨着，那么有一个边是重合的，这个边的长度就消失了，所以如果是两个格子挨着，总周长就是4*2 - 1*2。

4代表：每个格子的周长，是固定值

第一个2代表：黄色格子的数量，是变量

1代表：黄色格子重合的边数，是变量

第二个2代表：消失的数量，是固定值

可以再继续增加格子，规律都不会变，那么我们的重点就变成统计黄色格子的数量，以及黄色格子重合的边数。

如果数组中的元素为1代表黄色格子，那么统计黄色格子的数量，即是统计1的数量

统计黄色格子重合的边数，在做这个事情的时候，我们要选取一个方向，举个例子，第二排的前三个黄色格子，我们在第一个格子的视角来看，右边的格子有一条边跟他重合，在中间格子的视角来看，左右格子都有一条边跟他重合，在第三个格子的视角来看，左边的格子有一条边跟他重合。

那么我们不妨设定一个方向，从左到右，不回头看，依次从第一个格子，第二个格子，第三个格子的视角来看，只有2条边是重合的。

垂直方向的类似。

代码示例：

public void test() {
    int[][] grid = {{0, 1, 0, 0}, {1, 1, 1, 0}, {0, 1, 0, 0}, {1, 1, 0, 1}};
    // 记录岛屿的数量, 即数组中1的数量
    int count = 0;
    // 记录岛屿块之间重合的边数
    int num = 0;
    for (int i = 0; i < grid.length; i++) {
        for (int j = 0; j < grid[i].length; j++) {
            if (grid[i][j] == 1) {
                // 记录岛屿的数量+1
                count++;
                // 横向方向, 下一个节点是1, 则计数器+1
                if (i < grid.length - 1 && grid[i + 1][j] == 1) {
                    num++;
                }
                // 垂直方向, 下一个节点是1, 则计数器+1
                if (j < grid[i].length - 1 && grid[i][j + 1] == 1) {
                    num++;
                }
            }
        }
    }
    // 岛屿的周长 = 岛屿的数量 * 4 - 重合的边数 * 2
    int len = count * 4 - num * 2;
    System.out.println(len);
}

---

总结

注释已加好，抓紧练习，简单到有手就行！