排序算法(初阶)【冒泡,插入,选择排序】
文章目录
- 冒泡排序
- 冒泡排序原理
- 图解
- 冒泡排序算法名称由来
- 冒泡排序算法的时间复杂度
- 最好的情况
- 最坏的情况
- 冒泡排序代码
- 冒泡排序的稳定性
- 选择排序
- 选择排序的原理
- 图解
- 选择排序的时间复杂度
- 选择排序的代码
- 代码
- 选择排序的稳定性
- 插入排序
- 插入排序原理
- 图解
- 插入排序的时间复杂度
- 最好的情况
- 最坏的情况
- 插入排序的代码实现
- 插入排序的稳定性
冒泡排序
冒泡排序原理
比较相邻的两个元素。如果第一个比第二个大,就交换他们两个。
对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对,这被称为一趟冒泡排序
这样就可以把数组中要排序的数中的最大值放到最后,也相当于把一个元素排在了元素有序时它应处于的位置,它既然已经处于正确的位置就不需要在排这个元素了
所以下一趟冒泡排序就可以少排一个元素
针对所有的元素重复以上的步骤,除了最后一个。
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
一一一一一一一一一一一一一一一一一一一一
一一一一一一一一一一一一一一一一一一一一
图解
 由上图,冒泡排序每一趟都会把要排序元素中最大的冒到最后一个
由上图,冒泡排序每一趟都会把要排序元素中最大的冒到最后一个
一一一一一一一一一一一一一一一一一一一一
一一一一一一一一一一一一一一一一一一一一
冒泡排序算法名称由来
这个算法的名字由来是因为越大(小)的元素会经由交换慢慢“浮”到数列的顶端(升序或降序排列),就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样,故名“冒泡排序”。
一一一一一一一一一一一一一一一一一一一一
一一一一一一一一一一一一一一一一一一一一
冒泡排序算法的时间复杂度
最好的情况
要排升序(降序)时,要排序的元素已经是升序(降序),此时冒泡排序只是扫描了一遍要排序的元素,发现没有发生交换,就结束排序。
此时时间复杂度为N-1
一一一一一一一一一一一一一一一一一一一一
一一一一一一一一一一一一一一一一一一一一
最坏的情况
要排升序(降序)时,要列的元素是降序(升序)。
此时冒泡排序要排N-1趟
要排的元素个数从第一趟到最后一趟交换的次数为N-1,N-2,N-3…1
所以时间复杂度为1+2+3+…+N-1=(N^2-N)/2
所以冒泡排序平均的时间复杂度为O(N^2)
一一一一一一一一一一一一一一一一一一一一
一一一一一一一一一一一一一一一一一一一一
冒泡排序代码
//冒泡排序
void bubbleSort(int a[], int n)
{
int i = 0;
int j = 0;
int flag = 0;
//总共需要n趟冒泡排序
for (i = 0; i < n; i++)
{
//重置flag的值
flag = 0;
//一趟冒泡排序,排出一个最大值
for (j = 0; j < n - i - 1; j++)
{
if (a[j] > a[j + 1])
{
//交换
int tmp = a[j];
a[j] = a[j + 1];
a[j + 1] = tmp;
//只要一趟冒泡排序发生了交换,就还没排序完成
flag = 1;
}
}
//如果一趟冒泡排序之后,flag还是0,
//就说明没有交换,已经有序
if (flag == 0)
break;
}
}
一一一一一一一一一一一一一一一一一一一一
一一一一一一一一一一一一一一一一一一一一
冒泡排序的稳定性
冒泡排序就是把小的元素往前调或者把大的元素往后调。
比较是相邻的两个元素比较,交换也发生在这两个元素之间。
所以,如果两个元素相等,是不会再交换的;
如果两个相等的元素没有相邻,那么即使通过前面的两两交换把两个相邻起来,这时候也不会交换,所以相同元素的前后顺序并没有改变
所以冒泡排序是一种稳定排序算法。
一一一一一一一一一一一一一一一一一一一一
一一一一一一一一一一一一一一一一一一一一
选择排序
选择排序的原理
选择排序是一种简单直观的排序算法。它的工作原理是:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。
一一一一一一一一一一一一一一一一一一一一
一一一一一一一一一一一一一一一一一一一一
图解
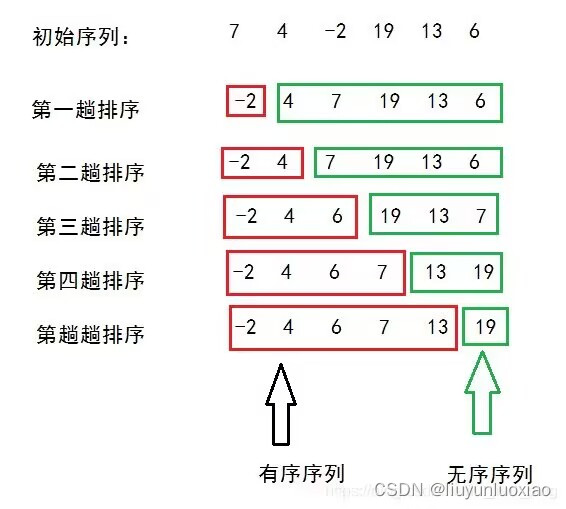 由上图,选择排序每一趟都选择一个无序数列中最小的放在有序数列末尾,直到无序序列的元素个数为1。
由上图,选择排序每一趟都选择一个无序数列中最小的放在有序数列末尾,直到无序序列的元素个数为1。
一一一一一一一一一一一一一一一一一一一一
一一一一一一一一一一一一一一一一一一一一
选择排序的时间复杂度
选择排序的交换操作介于 0 和 (n - 1)次之间。选择排序的比较操作为 n (n - 1) / 2 次之间。选择排序的赋值操作介于 0 和 3 (n - 1) 次之间。比较次数O(n^2),比较次数与关键字的初始状态无关,总的比较次数N=(n-1)+(n-2)+…+1=n*(n-1)/2。交换次数O(n),最好情况是,已经有序,交换0次;最坏情况交换n-1次,逆序交换n/2次。
所以选择排序的平均时间复杂度为O(N^2)
一一一一一一一一一一一一一一一一一一一一
一一一一一一一一一一一一一一一一一一一一
选择排序的代码
代码
//选择排序
void SelectSort(int a[], int n)
{
//count表示有序序列末尾的下标
int count= 0;
int i = 0;
//min为最小值的下标
int min = 0;
while(count<n)
{
//每一趟选择排序都从有序数列末尾开始找最小值
min = count;
for (i = count; i<n;i++)
{
if (a[min] > a[i])
min = i;
}
//Swap为交换函数
Swap(&a[count], &a[min]);
//每一趟选择排序之后有序数列末尾下标加一
count++;
}
}
一一一一一一一一一一一一一一一一一一一一
一一一一一一一一一一一一一一一一一一一一
选择排序的稳定性
在一趟选择排序中,如果一个元素比当前元素小,而该小的元素又出现在一个和当前元素相等的元素后面,那么交换后稳定性就被破坏了。
例如序列2,2,2,1,3
第一趟选择排序会把1与第一个2交换,导致原本应在前面的2跑到后面去了
所以选择排序是不稳定的
一一一一一一一一一一一一一一一一一一一一
一一一一一一一一一一一一一一一一一一一一
插入排序
插入排序原理
插入排序是指在待排序的元素中,假设前面n-1(其中n>=2)个数已经是排好顺序的,现将第n个数插到前面已经排好的序列中,然后找到合适自己的位置,使得插入第n个数的这个序列也是排好顺序的。按照此法对所有元素进行插入,直到整个序列排为有序的过程,称为插入排序。
插入排序的工作方式像许多人排序一手扑克牌。开始时,我们的左手为空并且桌子上的牌面向下。然后,我们每次从桌子上拿走一张牌并将它插入左手中正确的位置。为了找到一张牌的正确位置,我们从右到左将它与已在手中的每张牌进行比较。拿在左手上的牌总是排序好的,原来这些牌是桌子上牌堆中顶部的牌
一一一一一一一一一一一一一一一一一一一一
一一一一一一一一一一一一一一一一一一一一
图解
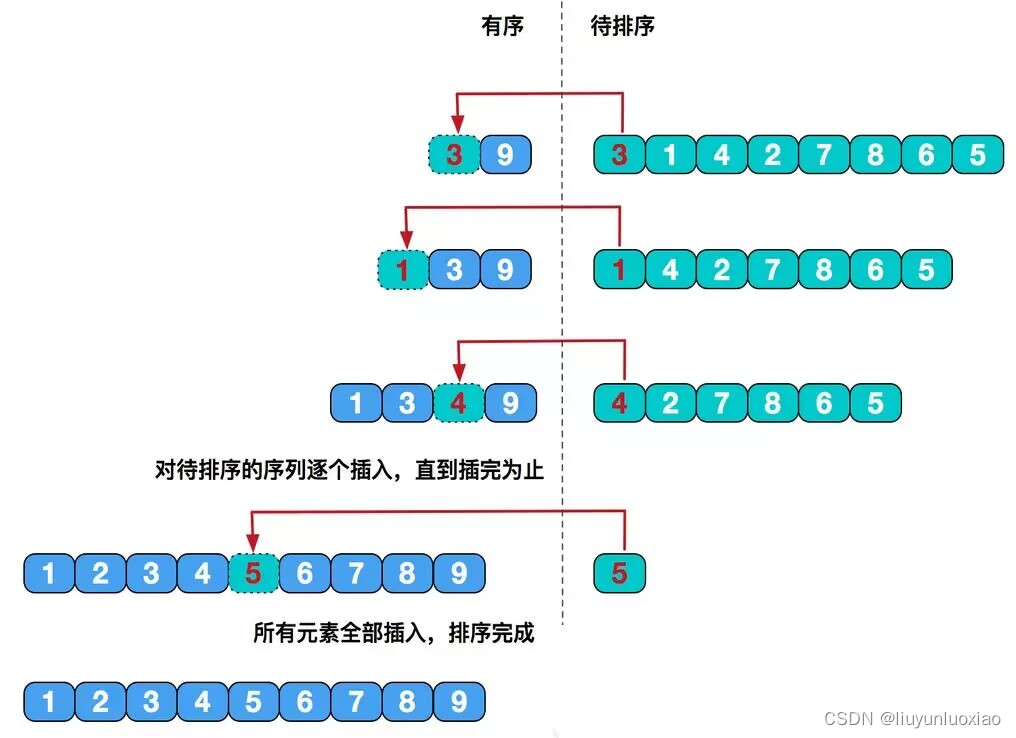
一一一一一一一一一一一一一一一一一一一一
一一一一一一一一一一一一一一一一一一一一
插入排序的时间复杂度
最好的情况
要排升序(降序)时,要排序的元素已经是升序(降序)
此时只需当前数跟前一个数比较一下就可以了,这时一共需要比较N- 1次
此时时间复杂度为O(N)
一一一一一一一一一一一一一一一一一一一一
一一一一一一一一一一一一一一一一一一一一
最坏的情况
要排升序(降序)时,要列的元素是降序(升序)。
此时总次数记为:1+2+3+…+N-1,所以,插入排序
最坏情况下的时间复杂度为O(N^2)
所以插入排序的平均时间复杂度为O(N^2)
一一一一一一一一一一一一一一一一一一一一
一一一一一一一一一一一一一一一一一一一一
插入排序的代码实现
//插入排序
void lnsertionSort(int a[], int n)
{
//end表示有序序列最末尾的元素的下标
int end = 0;
//tmp表示无序序列的第一个元素的下标
int tmp = 0;
//i控制插入排序的趟数
int i = 0;
for (i = 0;i < n - 1; i++)
{
end = i;
tmp = a[end + 1];
while (end >= 0)//end最小是0
{
if (a[end] > tmp)
{
//如果前一个大于后一个,就让前一个向后移一位
//给后一个可插入的空隙
a[end + 1] = a[end];
end--;
}
else
{
//因为是从已经有序的序列的末尾向前插入
//所以前一个之前的元素都比它小,所以不用再比较,直接结束循环
break;
}
}
a[end + 1] = tmp;
}
}
一一一一一一一一一一一一一一一一一一一一
一一一一一一一一一一一一一一一一一一一一
插入排序的稳定性
如果待排序的序列中存在两个或两个以上具有相同关键词的数据,排序后这些数据的相对次序保持不变,即它们的位置保持不变
所以插入排序是稳定的
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- BERT(从理论到实践): Bidirectional Encoder Representations from Transformers【2】
- Unity之角色控制器
- springboot(ssm甘肃旅游管理系统 在线旅游景点管理系统 Java系统
- 无监督关键词提取算法:TF-IDF、TextRank、RAKE、YAKE、 keyBERT
- 怎么制作电子邀请函_1分钟即可完成h5邀请函
- 基于改进凸优化算法的多机编队突防航迹规划
- 并发编程线程安全问题
- 前端浏览器滚动条炫酷美化
- C语言基础11 预处理和头文件
- 1.你好, Python!