[算法基础 ~排序] Golang 实现
文章目录
排序图片就不贴了吧
排序
什么是排序
以下部分动图来自CSDN
::: tip 稳定性的概念
定义:能保证两个相等的数,经过排序之后,其在序列的前后位置顺序不变。(A1=A2,排序前A1在A2前面,排序后A1还在A2前面)
意义:稳定性本质是维持具有相同属性的数据的插入顺序,如果后面需要使用该插入顺序排序,则稳定性排序可以避免这次排序。
:::
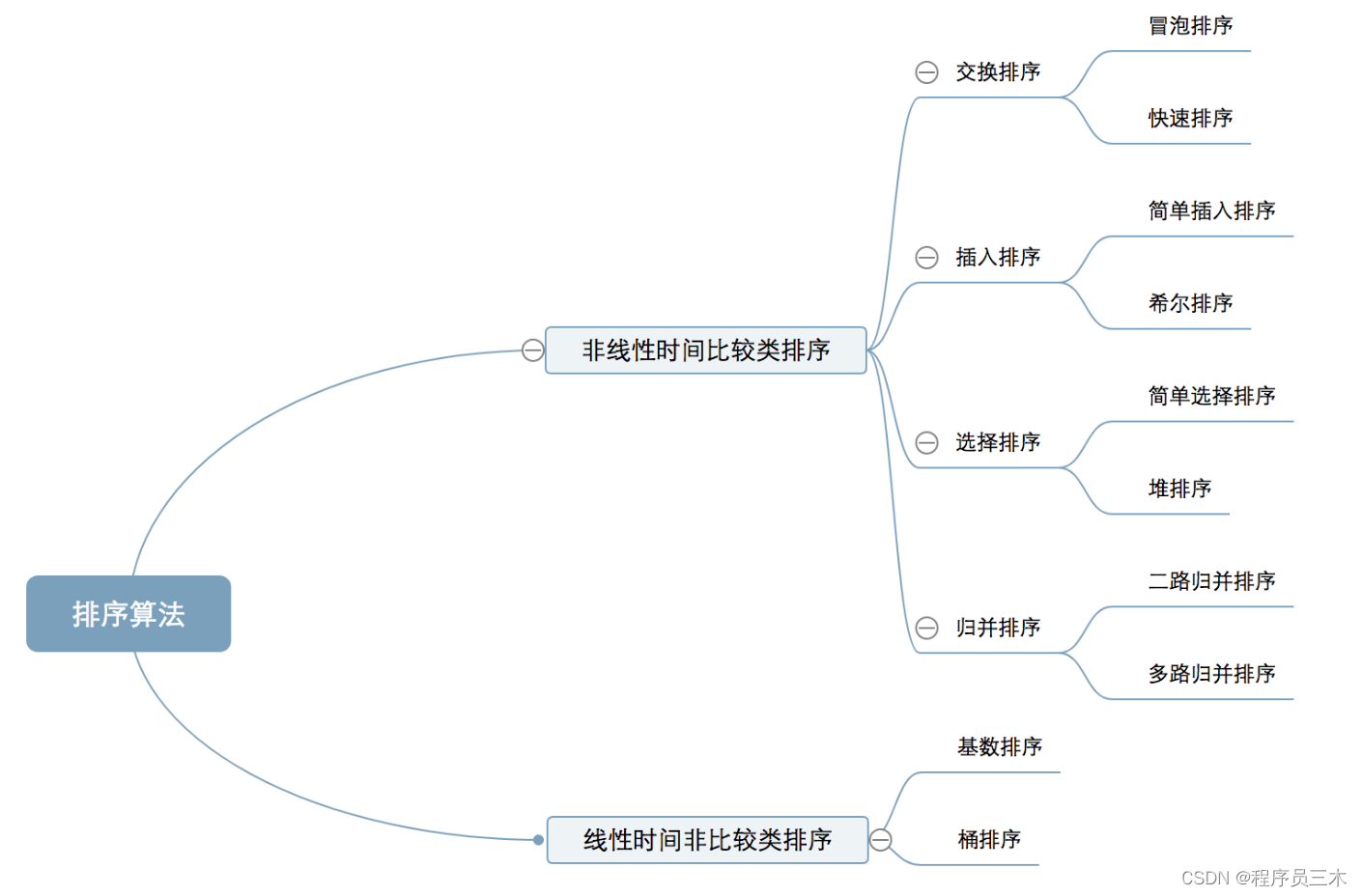
排序的分类
1. 冒泡
1.1 冒泡排序
- 一个一个往上冒
:::details 查看代码
func BubbleSort(arr []int) []int {
n := len(arr)
for i := 0; i < n-1; i++ {
for j := i + 1; j < n; j++ {
if arr[i] > arr[j] {
arr[i], arr[j] = arr[j], arr[i]
}
}
}
return arr
}
for(int i=0; i<k-1; i++)
for(int j=i+1; j<k; j++){
if(arr[j]<arr[i]){ // 从小到大
arr[i] ^= arr[j];
arr[j] ^= arr[i];
arr[i] ^=arr[j];
}
}
:::
1.2. 快速排序
-
升级版冒泡(
递归) -
基本思想
通过一趟排序将待排的数据分割成两部分,其中一部分的数据均比另一部分的数据要小,对两组数据进行排序。
:::details 查看代码
func QuickSort(a []int) []int {
n := len(a)
if n <= 1 {
return a
}
left := make([]int, 0)
right := make([]int, 0)
guard := a[0]
for i := 1; i < n; i++ {
if a[i] < guard {
left = append(left, a[i]) // 比哨兵小入左队
} else {
right = append(right, a[i]) // 其他入大队
}
}
left, right = QuickSort(left), QuickSort(right)
res := append(append(left, guard), right...)
return res
}
// 左闭右开
func QuickSort1(a []int, left, right int) {
if left >= right-1 {
return
}
low := left
high := right - 1
guard := a[low]
for low < high {
/*
小的往左,大的往右
*/
for low < high && a[high] >= guard {
high--
}
a[low] = a[high]
for low < high && a[low] <= guard {
low++
}
a[high] = a[low]
}
a[low] = guard
QuickSort1(a, left, low)
QuickSort1(a, low+1, right)
}
void q_sort(int a[], int left, int right){
// left, right 左闭右开, low、high闭区间
// a[left] 即左边第一个元素为哨兵
if(left >= right-1 ) return;
int low = left, high = right-1, center = a[low];
// 直到low==high 确保左边的元素都比右边的小
while( low < high ){
// 从右边开始往回搜索,找到第一个比哨兵小的元素,比哨兵大则跳过
while( low<high && a[high] >= center ) high --;
// 将比哨兵小的元素移动到左边
a[low] = a[high];
// 从左边往右边搜索, 找到第一个比哨兵大的元素,比哨兵小则跳过
while( low< high && a[low] <= center) low++;
// 将比哨兵大的元素移动到右边
a[high] = a[low];
}
// 把哨兵存入分界线位置
a[low] = center; // == a[high] = center;
// 开始递归快排
q_sort(a, left, low); // 左边
q_sort(a, low+1, right ); // 右边
}
快排优化版的简单示意图(以 3 5 2 1 6作为局部数组为例)
:::
2. 选择
2.1 简单选择排序
- 选择最小的往前放
:::details 查看代码
func SelectSort(a []int) []int {
n := len(a)
for i := 0; i < n-1; i++ {
minIndex := i
for j := i + 1; j < n; j++ {
if a[j] < a[minIndex] {
minIndex = j
}
}
if minIndex != i {
a[minIndex], a[i] = a[i], a[minIndex]
}
}
return a
}
// 从小到大
for(int i=0; i<length-1; i++){
minIndex=i;
for(int j=i+1; j<length{
if(arr[j]<arr[minIndex]) minIndex=j; // 选择最小的元素的下标
}
if( minIndex != i){
arr[i]^=arr[minIndex];
arr[minIndex] ^=arr[i];
arr[i] ^= arr[minIndex];
}
}
- 这里有一个小小的优化技巧
在搜索最小数下标的时候,同时搜索最大数的下标,可以使得复杂度减半。
:::
2.2 堆排序
::: details 先来了解下堆的相关概念:
堆是具有以下性质的完全二叉树:
每个结点的值都大于或等于其左右孩子结点的值,称为
大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。
如下图:
同时,我们对堆中的结点按层进行编号,将这种逻辑结构映射到数组中就是下面这个样子
该数组从逻辑上讲就是一个堆结构,我们用简单的公式来描述一下堆的定义就是:
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2] (小到大排序)
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2] (大到小排序)
:::
:::details 堆的百度百科
堆(heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。
堆总是满足下列性质:
- 堆中某个结点的值总是不大于或不小于其父结点的值;
- 堆总是一棵完全二叉树。
:::details 完全二叉树
- 完全二叉树的特点:
- 叶子结点只能出现在最下层和次下层,且最下层的叶子结点集中在树的左部。
需要注意的是,满二叉树肯定是完全二叉树,而完全二叉树不一定是满二叉树
- 判断一棵树是否是完全二叉树的思路
1>如果树为空,则直接返回错
2>如果树不为空:层序遍历二叉树
2.1>如果一个结点左右孩子都不为空,则pop该节点,将其左右孩子入队列;
2.1>如果遇到一个结点,左孩子为空,右孩子不为空,则该树一定不是完全二叉树;
2.2>如果遇到一个结点,左孩子不为空,右孩子为空;或者左右孩子都为空,且则该节点之后的队列中的结点都为叶子节点,该树才是完全二叉树,否则就不是完全二叉树.
:::
了解了这些定义。接下来看看堆排序的基本思想及基本步骤:
- 堆排序基本思想及步骤
基于选择排序
堆排序的基本思想是:将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了
:::details 查看代码
// 构建小顶堆, 大到小排序
// 交互a数组中的x跟y
void swap(int a[], int x, int y){
a[x] ^= a[y];
a[y] ^= a[x];
a[x] ^= a[y];
}
// 调整堆
void heapAdjust(int a[], int i, int len){
int flag = a[i];
for(int j=2*i; j<=len; j*=2 ){
if( j<len && a[j]>a[j+1] ) ++j;
if( flag < a[j] ) break;
a[i] = a[j]; i=j;
}
a[i] = flag;
}
// 堆排序
void heapSort(int a[], int len){
for(int i=len/2; i>0; --i){
heapAdjust(a, i, len);
}
for(int i=len; i>1; i--){
swap(a, 1, i);
heapAdjust(a, 1, i-1);
}
}
:::
3. 插入
::: tip 与现实场景的联系
存在一个已经排好的队伍(从矮到高),这时,来了个还没排的家伙,他需要去找他需要站的位置。
:::
3.1 直接插入
- 从后往前, 默认前面已排好序
- 假设
j前面j-1的元素已经是有序的,接下来要对a[j]的位置查找
:::details 查看代码
func InsertSort(a []int) []int {
n := len(a)
for i := 1; i < n; i++ {
for j := i; j > 0 && a[j] < a[j-1]; j-- {
a[j-1], a[j] = a[j], a[j-1]
}
}
return a
}
// 从小到大
for(int i=1; i<length; i++){
for(int j=i; (j>0) && ( arr[j]<arr[j-1] ); j--){
arr[j]^=arr[j-1];
arr[j-1] ^= arr[j];
arr[j] ^=arr[j-1];
}
}
:::
3.2 折半插入
从1开始,对后面的元素进行折半查找插入
:::details 查看代码
func BinarySearchInsertSort(a []int) []int {
n := len(a)
var low, high, mid, reg int
for i := 1; i < n; i++ {
low = 0
high = i - 1
reg = a[i]
for low <= high {
mid = (low + high) >> 1
if reg > a[mid] {
low = mid + 1
} else {
high = mid - 1
}
}
/*
low是还没排序的元素应该去的位置,所以low后面已排序的元素都要往后站
*/
for j := i; j > low; j-- {
a[j] = a[j-1]
}
a[low] = reg
}
return a
}
// 降序(从大到小)
void z_sort(int a[], int len){
int low = 0,high = 0,mid;
int temp = 0;
for (int i=1; i<len; i++) {
low=0;
high=i-1;
temp=a[i]; // 要插入的元素
while (low<=high) {
mid=(low+high)>>1;
// 决定顺序的位置
if (a[mid]<temp) {
high=mid-1;
}else{
low=mid+1;
}
}
// 把元素后移
for (int j=i; j>low; j--) {
a[j]=a[j-1];
}
a[low]=temp;//插入元素
}
}
:::
3.3 希尔排序
::: tip 百度百科
希尔排序(Shell’s Sort)是插入排序的一种又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因 D.L.Shell 于 1959 年提出而得名。
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至 1 时,整个文件恰被分成一组,算法便终止。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
- 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率。
- 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位。
:::
希尔排序是把记录按下标的一定增量
分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
- 重点:注意对每个子序列进行插入排序
:::details 查看代码
func shellSort(a []int) []int {
n := len(a)
/*
@gap: 增量每次减半
*/
for gap := n >> 1; gap >= 1; gap >>= 1 {
for i := gap; i < n; i += gap {
for j := i; j > 0 && a[j] < a[j-gap]; j -= gap {
a[j-gap], a[j] = a[j], a[j-gap]
}
}
}
return a
}
void shellSort(int* a, int n)
{
int i,gap,j;
// gap为步长,每次减为原来的一半。
for (gap = n / 2; gap >=1 ; gap /= 2)
{
// 组内排序
for (i = gap ;i < n; i+= gap) {
for(j = i; j>0 && a[j] < a[j-gap]; j-= gap) {
swap(a[j-gap], a[j]);
}
}
}
}
:::
4. 归并排序
- 基本思想
归并排序是用分治思想,分治模式在每一层递归上有三个步骤:
- 分解(Divide):将n个元素分成个含n/2个元素的子序列。
- 解决(Conquer):用合并排序法对两个子序列递归的排序。
- 合并(Combine):合并两个已排序的子序列已得到排序结果。
- 实现逻辑
2.1 迭代法
① 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
② 设定两个指针,最初位置分别为两个已经排序序列的起始位置
③ 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
④ 重复步骤③直到某一指针到达序列尾
⑤ 将另一序列剩下的所有元素直接复制到合并序列尾
2.2 递归法
① 将序列每相邻两个数字进行归并操作,形成floor(n/2)个序列,排序后每个序列包含两个元素
② 将上述序列再次归并,形成floor(n/4)个序列,每个序列包含四个元素
③ 重复步骤②,直到所有元素排序完毕
-
动图演示
-
归并排序演示
具体的我们以一组无序数列{14,12,15,13,11,16}为例分解说明,如下图所示:
上图中首先把一个未排序的序列从中间分割成2部分,再把2部分分成4部分,依次分割下去,直到分割成一个一个的数据,再把这些数据两两归并到一起,使之有序,不停的归并,最后成为一个排好序的序列。
- 文字版
:::details
有序数组A:[3 8 9 11 13]
有序数组B:[1 5 8 10 17 19 20 23]
[] 表示比较的范围。
因为 1 < 3,所以 1 加入辅助数组
有序数组A:[3 8 9 11 13]
有序数组B:1 [5 8 10 17 19 20 23]
辅助数组:1
因为 3 < 5,所以 3 加入辅助数组
有序数组A:3 [8 9 11 13]
有序数组B:1 [5 8 10 17 19 20 23]
辅助数组:1 3
因为 5 < 8,所以 5 加入辅助数组
有序数组A:3 [8 9 11 13]
有序数组B:1 5 [8 10 17 19 20 23]
辅助数组:1 3 5
因为 8 == 8,所以 两个数都 加入辅助数组
有序数组A:3 8 [9 11 13]
有序数组B:1 5 8 [10 17 19 20 23]
辅助数组:1 3 5 8 8
因为 9 < 10,所以 9 加入辅助数组
有序数组A:3 8 9 [11 13]
有序数组B:1 5 8 [10 17 19 20 23]
辅助数组:1 3 5 8 8 9
因为 10 < 11,所以 10 加入辅助数组
有序数组A:3 8 9 [11 13]
有序数组B:1 5 8 10 [17 19 20 23]
辅助数组:1 3 5 8 8 9 10
因为 11 < 17,所以 11 加入辅助数组
有序数组A:3 8 9 11 [13]
有序数组B:1 5 8 10 [17 19 20 23]
辅助数组:1 3 5 8 8 9 10 11
因为 13 < 17,所以 13 加入辅助数组
有序数组A:3 8 9 11 13
有序数组B:1 5 8 10 [17 19 20 23]
辅助数组:1 3 5 8 8 9 10 11 13
因为数组A已经没有比较元素,将数组B剩下的元素拼接在辅助数组后面。
结果:1 3 5 8 8 9 10 11 13 17 19 20 23
:::
代码实现
- 自顶向下归并(递归)
:::details 查看代码
// 二路归并
func MergeSort(a []int) []int {
n := len(a)
if n <= 1 {
return a
}
mid := n >> 1
left, right := MergeSort(a[:mid]), MergeSort(a[mid:])
return merge(left, right)
}
func merge(left, right []int) (res []int) {
l, r := 0, 0
len_l, len_r := len(left), len(right)
for l < len_l && r < len_r {
if left[l] < right[r] {
res = append(res, left[l])
l++
} else {
res = append(res, right[r])
r++
}
}
// 把两个子切片的剩余元素直接入队
res = append(append(res, left[l:]...), right[r:]...)
return
}
// 归并排序(C-递归版)
void merge_sort_recursive(int arr[], int reg[], int start, int end) {
if (start >= end)
return;
int len = end - start, mid = (len / 2) + start;
int start1 = start, end1 = mid;
int start2 = mid + 1, end2 = end;
merge_sort_recursive(arr, reg, start1, end1);
merge_sort_recursive(arr, reg, start2, end2);
int k = start;
// 决定是降序还是升序
while (start1 <= end1 && start2 <= end2)
reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
while (start1 <= end1)
reg[k++] = arr[start1++];
while (start2 <= end2)
reg[k++] = arr[start2++];
for (k = start; k <= end; k++)
arr[k] = reg[k];
}
void merge_sort(int arr[], const int len) {
int *reg = new int[len+1];
merge_sort_recursive(arr, reg, 0, len - 1);
delete[] reg;
}
:::
- 自底向上归并(迭代)
:::details 查看代码
func MergeSort(a []int, begin, end int) {
step := 1
// 步数为1开始,step长度的数组表示一个有序的数组
// 1 -> 2 -> 4 -> 8
for end-begin > step {
// 从头到尾对数组进行归并操作
// step << 1 = 2 * step 表示偏移到后两个有序数组将它们进行归并
for i := begin; i < end; i += step << 1 {
low := i
mid := low + step
high := low + (step << 1)
// 不存在第二个数组,直接返回
if mid > end {
return
}
// 第二个数组长度不够
if high > end {
high = end
}
// 合并两个有序的数组
merge(a, low, mid, high)
}
step <<= 1
}
}
func merge(a []int, begin, mid, end int) {
leftSize := mid - begin
rightSize := end - mid
newSize := leftSize + rightSize
result := make([]int, 0, newSize)
l, r := 0, 0
for l < leftSize && r < rightSize {
lval := a[begin+l]
rval := a[mid+r]
if lval < rval {
result = append(result, lval)
l++
} else {
result = append(result, rval)
r++
}
}
result = append(result, a[begin+l:mid]...)
result = append(result, a[mid+r:end]...)
for i := 0; i < newSize; i++ {
a[begin+i] = result[i]
}
return
}
void mergeSort(int a[], int reg[], const int end){
// 分
for(int step=1; step<end; step*=2){
for(int j=0; j < end; j += step*2 ){
int low = j, mid = j+step-1, high = min(j+2*step-1, end-1);
merge(a, reg, low, mid, high );
}
}
}
void merge(int a[], int reg[], int l, const int mid, const int r){
int start = l;
int end = r;
int j = mid+1;
int i = l;
while( i<= mid && j<= r ){
reg[l++] = a[i]>=a[j] ? a[i++] : a[j++];
}
while(i<=mid) reg[l++] = a[i++];
while(j<=r) reg[l++] = a[j++];
for(int ii=start; ii<=end; ii++){
a[ii] = reg[ii];
}
}
:::
5. 基数排序
:::details 查看代码
func getbits(a []int) int {
max_num := 0
for _, v := range a {
if v > max_num {
max_num = v
}
}
res := 0
if max_num == 0 {
return 1
}
for max_num > 0 {
max_num /= 10
res++
}
return res
}
func radixSort(a []int) {
n := len(a)
step := getbits(a)
radix := 1
var num, tail int
reg := make([][]int, 10)
for i := 0; i < step; i++ {
radix *= 10
// 每一轮都要清空桶
for i := 0; i < 10; i++ {
reg[i] = make([]int, 0)
}
for j := 0; j < n; j++ {
num = a[j] % radix
tail = num / (radix / 10)
reg[tail] = append(reg[tail], a[j])
}
index := 0
for k := 0; k < 10; k++ {
for _, v := range reg[k] {
a[index] = v
index++
}
}
}
}
#include<iostream>
using namespace std;
int maxbit(int data[], int n) //辅助函数,求数据的最大位数
{
int d = 1; //保存最大的位数
int p = 10;
for(int i = 0; i < n; ++i)
{
while(data[i] >= p)
{
p *= 10;
++d;
}
}
return d;
}
void radixSort(int data[], int n) //基数排序
{
// d 位
int d = maxbit(data, n);
int *tmp = new int[n+5];
int *count = new int[10]; //计数器 --> 排序桶
int *flag = new int[10];
int i, j, k;
int radix = 1;
for(i = 1; i <= d; i++) //进行d次排序
{
for(j = 0; j < 10; j++){
count[j] = 0; //每次分配前清空计数器(清桶)
tmp[j] = -1;
flag[j] = 0;
}
for(j = 0; j < n; j++)
{
// k 是当前数字位置中的数字
k = (data[j] / radix) % 10; //统计每个桶中的记录数
count[k]++;
}
for(int jj=0; jj<10; jj++){
flag[jj] = count[jj];
}
for(j = 1; j < 10; j++)
count[j] = count[j - 1] + count[j]; //将tmp中的位置依次分配给每个桶
for(j = n - 1; j >= 0; j--) //将所有桶中记录依次收集到tmp中
{
k = (data[j] / radix) % 10;
tmp[count[k] - 1] = data[j];
count[k]--;
}
for(j = 0; j < n; j++){//将临时数组的内容复制到data中
data[j] = tmp[j];
}
radix = radix * 10;
}
delete[]tmp;
delete[]count;
}
:::
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 超级快充充电头设计
- Python count()方法:统计字符串出现的次数与字符串拼接(包含字符串拼接数字)
- 达梦到达梦的外部链接dblink(DM-DM DBLINK)
- 免费WPML v4.6.6已注册学习版+17插件包
- Creo各版本安装指南
- 【Proteus仿真】【51单片机】定时智能插座开关
- 2D变换的知识点
- 简单几步就可以轻松去除图片水印
- 【Leetcode】重排链表、旋转链表、反转链表||
- 02-JVM内存模型深度剖析与优化