每日一道算法题day-one(备战蓝桥杯)
从今天开始博主会每天做一道算法题备战蓝桥杯,并分享博主做题的思路,有兴趣就加入我把!
算法题目:
有一个长度为?N? 的字符串?S ,其中的每个字符要么是?B,要么是?E。
我们规定?S??的价值等于其中包含的子串?BB?以及子串?EE?的数量之和。
例如,BBBEEE?中包含?22?个?BB?以及?22?个?EE,所以?BBBEEE?的价值等于?44。
我们想要计算?S??的价值,不幸的是,在我们得到?S?之前,约翰将其中的一些字符改为了?F。
目前,我们只能看到改动后的字符串?S对于其中的每个?F,我们并不清楚它之前是?B?还是?E。
请你计算,改动前的?S?有多少种可能的价值并将所有可能价值全部输出。
输入格式
第一行包含一个整数?N。
第二行包含改动后的字符串?S。
输出格式
第一行输出一个整数?K,表示改动前的?S?的可能价值的数量。
接下来?K?行,按照升序顺序,每行输出一个可能价值。
输入样例1:
4
BEEF
输出样例1:
2
1
2
输入样例2:
9
FEBFEBFEB
输出样例2:
2
2
3
输入样例3:
10
BFFFFFEBFE
输出样例3:
3
2
4
6?思路:
我们看字符串的F和E太过于麻烦,我们给抽象成01字符串,更清晰的看出关系
现在有这样一段字符串:
xx01xxx0010xxx011xx110
这段字符串中,有四段x组成的子字符串,而这四段子字符串,都是相互独立的,修改其中任意一端,都不会影响到其他三段的数值,所以我们可以把这四段各自对应的情况拿出来单独讨论,最后再合并到一起,就能求出答案:
步骤:
第一步,先分析每一段连续的x的价值有哪些。
第二步,再分析所有段的价值之和有哪些
k为x的数量
情况1:xxxxx?
长度为五的x,最多有四个相邻对,所以最大值是4,最小值自然是0 ?取值:0,1,2,……,k-1
情况2:(0xxxxx/1xxxxx)/(xxxxx0/xxxxx1)?
当我们x全取取相邻相同的数时,最大值就是k,最小值是0
取值:0,1,2,……,k
情况3:0xxxxxx0/1xxxxxx1?
最多就是都取成一样的 :k+1个 最少 :0个
但是我们中间画五个x最少是0个,但是如果中间是偶数呢,大家自己模拟一下,最少就会有一个,所以情况三就要分情况
最多: k+1
最少: ? ? ? k+1是偶数:0?
?? ? ? k+1是奇数:1
大家自己画图模拟一下很明了
现在要最大和最小都有了,自然要考虑中间的数能不能取到,每当我们改变一个数,就会改变两个数对的值,所以可以取值的数就是公差为2的等差数列
所以取值:k+1,k-1,k-3,……,0/1(取决于k的奇偶性)
第四种情况: 0xxxxx1/1xxxxx0 ?最多k个,和左边或者右边相同,
最小依旧是分情况讨论:
?? ??? ??? ?k是偶数: 0个
?? ??? ??? ?k是奇数: 1个
都是画图,通俗易懂
取值:每改变一个x,影响周围的两数对,所以取值依旧是公差为2的等差数列
k,k-2,k-4,……,1/0(取决k的奇偶性)
现在我们把每一种情况和段落都分析完了,可以进行合并了
问题1:如果我们合并两个公差为2的等差数列,会得到什么样的结果:
答案:会得到一个新的公差为2的等差数列,最小值是两个数列的最小值相加,最大值是两个数列的最大值相加
问题二:如果我们合并一个公差为2的等差数列和一个公差为1的等差数列,会得到什么样的结果?
答案,会得到一个公差为一的等差数列,最小值最大值同上
最终做法:
第一步:先求中间段。
第二步:再求两边的段
第三步:合并第一步和第二步的结果
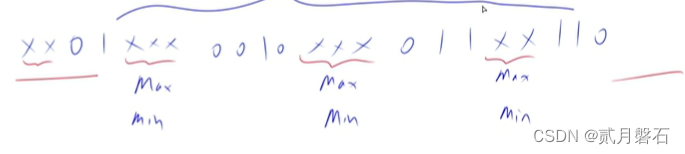
?
?题解代码:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int n;
string s;
int main()
{
cin >> n >> s;
if (s == string(n, 'F'))
{
cout << n << endl;
for (int i = 0; i < n; i ++ )
cout << i << endl;
}
else
{
int l = 0, r = n - 1;
while (s[l] == 'F') l ++ ;
while (s[r] == 'F') r -- ;
int low = 0, high = 0;
auto str = s;
for (int i = l; i <= r; i ++ )
{
if (str[i] == 'F')
{
if (str[i - 1] == 'B') str[i] = 'E';
else str[i] = 'B';
}
if (i > l && str[i] == str[i - 1]) low ++ ;
}
str = s;
for (int i = l; i <= r; i ++ )
{
if (str[i] == 'F') str[i] = str[i - 1];
if (i > l && str[i] == str[i - 1]) high ++ ;
}
int ends = l + n - 1 - r, d = 2;
if (ends) high += ends, d = 1;
cout << (high - low) / d + 1 << endl;
for (int i = low; i <= high; i += d)
cout << i << endl;
}
return 0;
}
这是完全根据题解写的代码,其实其中一种思路,大家可以参考一下,也可以自己按照思路写代码,如果看不懂的话可以在评论区指出或者私信博主
对大家有帮助的话不要吝啬手里的点赞关注呀,以后每天博主都会带来优质内容。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【关于Java的堆空间和堆内存】
- 【飞凌 OK113i-C 全志T113-i开发板】测试实时系统
- 聊一聊 .NET高级调试 内核模式堆泄露
- 北京大学漏洞报送证书
- java智慧工地系统:让工地管理可视化、数字化、智能化
- SIT75176B:3.0~5.5V 供电,32 节点,10Mbps 半双工 RS485/RS422 收发器
- 你还没脱单,这些软件都得背锅
- 大模型介绍2:核心技术(未完待续)
- 使用 Layui 的 template 模块来动态加载select选项
- 查询最新的3条数据,总和,最小值,有判定条件