[PyTorch][chapter 11][李宏毅深度学习][Semi-supervised Learning]

发布时间：2024年01月23日

前言：

? ? ?这里面简介一下半监督学习，如何利用未打标签的数据集。

重点可以参考一下?? Graph-based Approach 方案。

目录：

  1. ? ?简介
  2. ? ?Semi-supervised Learning for Generative Model
  3. ? ?low-density Separation?Assumption
  4. ? ?Entropy-based Regularization
  5. ? ?semi-supervised SVM
  6. ? ?Smoothness Assumption
  7. ? Graph-based Approach

一 简介

? ? ?假设我们已经有了R 组有标签的数据集

? ? ?\begin{Bmatrix} (x^r,\hat{y}^r) \end{Bmatrix}_{i=1}^{R}

? ? 还有u 组未打标签的数据集

? ? ?\begin{Bmatrix} (x^r) \end{Bmatrix}_{j=R}^{R+U}

? ? ?u\geq R

? ? 如何利用这些未打标签的数据训练模型,?称为半监督学习

? ?半监督学习分为两类

? ? transductive learning(直推式学习):
?? ?unabeled data is the testing data
? ?

? ?Inductive learning(归纳推理 学习)
? ? unabeled data is not the testing data

? ?1.1? 为什么需要半监督学习

? ? ? ? ? 现实生活中,存在大量未打标签的数据集，需要充分利用这种未打标签的数据集

对模型性能的提升非常有帮助.

? 1.2 为什么半监督学习对分类有帮助呢？

? ??

? ? ? ? 未打标签的数据集分布也可以用于模型分类.如上图分类猫狗的例子：

? ? 如果只考虑背景颜色（蓝色,橙色点）其分类边界是红色。 但是加入

灰色的未打标签的数据集进行考虑，分类边界就会发生变化.

?

二??Semi-supervised Learning for Generative Model

? ? ? 预置条件：

? ? ? 根据已有的标签集得到

? ? ??\theta=\begin{Bmatrix} {p(c_1),p_(c_2),u^1,u^2,\sum} \end{Bmatrix}

? ? ?迭代流程：

? ? ? ? ? ? E步? step1 :? 计算未打标签的数据集后验概率（posterior probability）

? ? ? ? ? ? ? ? ? ? ? ??P_{\theta}(c_1|x^u)

? ? ? ? ? ? M步：step2:? 更新模型,计算先验概率

? ? ? ? ? ? ? ? ? ? ??p(c_1)=\frac{N_1+\sum_{x}p(c_1|x^u)}{N}

? ? ? ? ? ? ? ? ? ? ? step3: 计算

? ? ? ? ? ? ? ? ? ? ? u^1=\frac{1}{N_1}\sum_{x^r \in c_1}x^r+\frac{1}{\sum_{x^u}P(c_1|x^u)}\sum_{x^u}p(c_1|x^u)x^u

? ? ? ? ? ? ? ? ? ? ?反复迭代 step1-step3,知道?u^1,p(c^1)?不再发生变化? ?

?它的理论基础是极大似然估计,对于有标签的数据集：

? ? ? ?L(\theta)=\sum_{x^r}logP_{\theta}(x^r, \hat{y^r})

针对有标签和无标签的数据集：

? ? ??log L(\theta)=\sum_{x^r}log P_{\theta}(x^r,\hat{y^r})+\sum_{x^u}logP_{\theta}(x^u)

其中

p_{\theta}(x^u)=p_{\theta}(x^u|c_1)p(c_1)+p_{\theta}(x^u|c_2)p(c_2)

三? low-density Separation?

? ? 其典型的代表是self-train

? ? 1:? ?通过已打过标签的数据集训练模型，得到分类器f^{*}

? ? 2:? ? 应用分类器f^{*},对未打标签的数据集进行分类，得到

? ? ? ? ? ??\begin{Bmatrix} (x^u,y^u) \end{Bmatrix}_{u=l}^{u+R},得到伪标签

? ? 3：? 从未打标签的数据集中，选择一部分置信度高的添加到已打

? ? ? ? ? 标签的数据集中,重新训练模型

? 但是做回归算法的时候，不能使用该方案，做分类的时候，

采用Hard-label 方案

? ? ? ? ? ? ? ??

四? Entropy-based Regularization

? ? ?这种方案在训练的时候，直接加入unlabeled data 作为正规化项。

我们训练得到的模型，期望其在unlabeled data上面的Entropy 越小越好

（代表其某一类分类概率特别高）

五? ?semi-supervised SVM


半监督SVM的数学步骤可以分为以下几个步骤：

步骤1：构建初始分类器
? ? ? ? 首先，我们使用少量的标记数据来构建一个初始的支持向量机分类器。这个分类器将在已知数据上找到一个良好的决策边界.

步骤2：利用未标记数据
? ? ? ? ?然后，我们引入未标记数据。未标记数据不会直接影响初始分类器的决策边界，但它们会在训练过程中起到重要作用.

步骤3：半监督优化
? ? ? ? ? ?半监督SVM通过考虑未标记数据的分布，调整决策边界以提高分类性能。这通常通过引入正则化项来实现，以平衡标记数据和未标记数据的影响.

步骤4：重复迭代
? ? ? ? ? ? ?我们重复执行半监督优化的过程，直到达到预定的迭代次数或决策边界稳定。这个过程将最大化分类性能，并充分利用未标记数据
————————————————
原文链接：https://blog.csdn.net/DeepViewInsight/article/details/132958722

?30:25 秒

? ? ? ? ?

?六?? Smoothness Assumption

? ?问题：

? ? ?x^1,x^3?已经打过标签了,?x^2未打标签，

? ? ?x^2到底打成x^1,?还是?x^3?的标签

? ? 解决方案：

这种假设是基于：x^1,x^2之间有大量联通区域（high density region）,

所以x^2标签可以认为和x^1相同.

?

6.1 例子

?如上图，中间2 可以通过右边的2经过一系列的变化得到（中间有联通的区域），

但是中间2 无法经过变化得到右边的3 ，所以其标签为2

6.2实践操作原理：

? ? ? ?1? ? 通过AE 编码器对已打标签的图像数据进行降维，

? ? ? ?2? 通过AE 编码器对输入未打标签的图形进行降维

? ? ? ?3? 最后对降维后的数据集 观察是否有联通区域进行打标签。

七? Graph-based Approach

?7.1? 问题：

? ? ?

? ? ?如何判断x^1,x^2之间有高密度连接区域，通过graph 来表示数据。

定义s?来判断x^1,x^2之间的相似度。

? ? ?添加edge:? k? 最邻近点

? ? ? ? ? ? ? ? ? ? ? ? e-邻近点

? ? ? ?

?

? ? ?7.2 相似度函数

? ? ? ? ??S=\frac{1}{N}\sum_{i,j}W_{i,j}(y^i,y^j)^2(针对所有所有数据,无论是打标签还是未打标签

? ? ? ? ? 如下图

?

? ? 7.3?这张图是如何计算出来的

? ? ? ? 左图：S=0.5

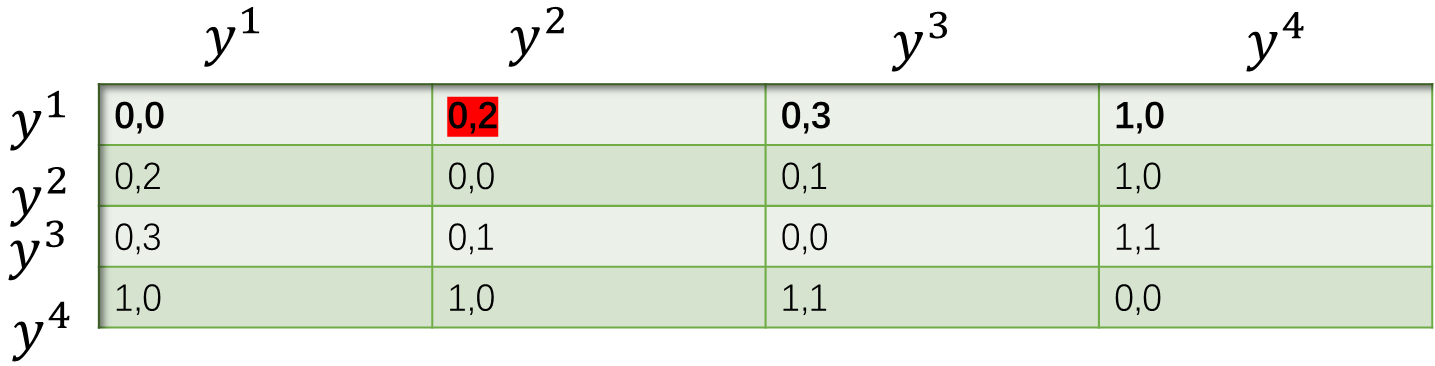
? ? 可以通过矩阵表示,比如红色部分

? ?0：y^1-y^2=1-1=0

? ?2:??w_{1,2}=2? ?

? ?把矩阵里面每个格子里面的元素相乘求和，再处于4(N=4)

S=\begin{pmatrix} 0*0+0*2+0*3+1*0\\ 0*2+0*0+0*1+1*0 \\ 0*3+0*1+0*0+1*1 \\ 1*0+1*0+1*1+0*0 \end{pmatrix}/4

? ? ?=0.5

右图：S=3

S=\begin{pmatrix} 0*0+1*2+1*3+0*0\\ 1*2+0*0+0*1+1*0 \\ 1*3+0*1+0*0+1*1 \\ 0*0+1*0+1*1+0*0 \end{pmatrix}/4

? ? ?=3

?7.4? 矩阵计算方式

? ? ? ? ? ?S=\frac{1}{N}\sum_{i,j}(y^i-y^{j})^2=y^TLy

? ? ? ? ? ?y:(R+U)-dim vector

? ? ? ? ? ? ? ? ? ??y=[...y^i...y^{j}...]^T

? ? ? ? ? ?L:? (R+U)*(R+U) matrix? ?

? ? ? ? ? L=D-W? ? ? ? ? ? ?

? 证明如下：

??W=\begin{bmatrix} w_{11} &w_{12} &... & w_{1n}\\ w_{21} &w_{22} &... &w_{2n} \\ ... & ...& ... &.. \\ w_{n1}& w_{n2} &... &w_{nn} \end{bmatrix}

??D=\begin{bmatrix} \sum_{j}w_{1,j} & 0 & .. & 0\\ & \sum_{j}w_{2,j} & & \\ & &... & \\ & & & \sum_{j}w_{n,j} \end{bmatrix}

y^TLy=y^TDy-y^TWy

?其中

y^TDy= \begin{bmatrix} y_1\sum_{j}w_{1,j} &y_2\sum_{j}w_{2,j} &... & y_n\sum_{j}w_{n,j} \end{bmatrix}\begin{bmatrix} y_1\\ y_2 \\ .... \\ y_n \end{bmatrix}

? ? ? ? ? ? ? ?=y_1^2\sum_{j}w_{1,j}+y_2^2\sum_{j}w_{2,j}+...+y_n^2\sum_{j}w_{2,j}

? ? ? ? ? ? ??=\sum_{i,j}y_i^2w_{i,j}

y^TWy=\begin{bmatrix} \sum_{i}y_iw_{i,1}, & \sum_{i}y_iw_{i,2} & ....& \sum_{i}y_iw_{i,n} \end{bmatrix}\begin{bmatrix} y_1\\ y_2 \\ .... \\ y_n \end{bmatrix}

? ? ? ? ? ? ??=y_1\sum_{i}y_iw_{i,1}+y_2\sum_{i}y_iw_{i,2}+...+y_n\sum_{i}y_iw_{i,n}

? ? ? ? ? ? ? ?=\sum_{i,j}y_iy_jw_{ij}

所以

y^TLy=y^TDy-y^TWy

=\sum_{i,j}(y_i^2-y_{ij})W_{ij}

=\frac{1}{2}\sum_{ij}(2y_i^2-2y_{ij})W_{ij}(i,j的维度相同,数据的标签）

=\frac{1}{2}\sum_{ij}(y_i^2+y_j^2-2y_{ij})W_{ij}

=\frac{1}{2}\sum_{i,j}(y_i-y_j)^2W_{i,j}

7.5 利用未打标签的数据集重新定义损失函数

参考：

深入半监督学习：半监督支持向量机（Semi-Supervised SVM）_semi_supervised-CSDN博客

使用pytorch实现高斯混合模型分类器 - 知乎

机器学习——概率分类(三)高斯概率密度与混合高斯模型_概率密度分类-CSDN博客

12: Semi-supervised_哔哩哔哩_bilibili

（二）Semi-supervised（半监督学习）李宏毅-CSDN博客

2020李宏毅学习笔记—— 10. Semi-supervised Learning（半监督学习）_semi-supervised few-shot learning via multi-factor-CSDN博客

文章来源:https://blog.csdn.net/chengxf2/article/details/135534348
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章