数据结构之各大排序（C语言版）
发布时间：2024年01月05日
我们这里话不多说，排序重要性大家都很清楚，所以我们直接开始。
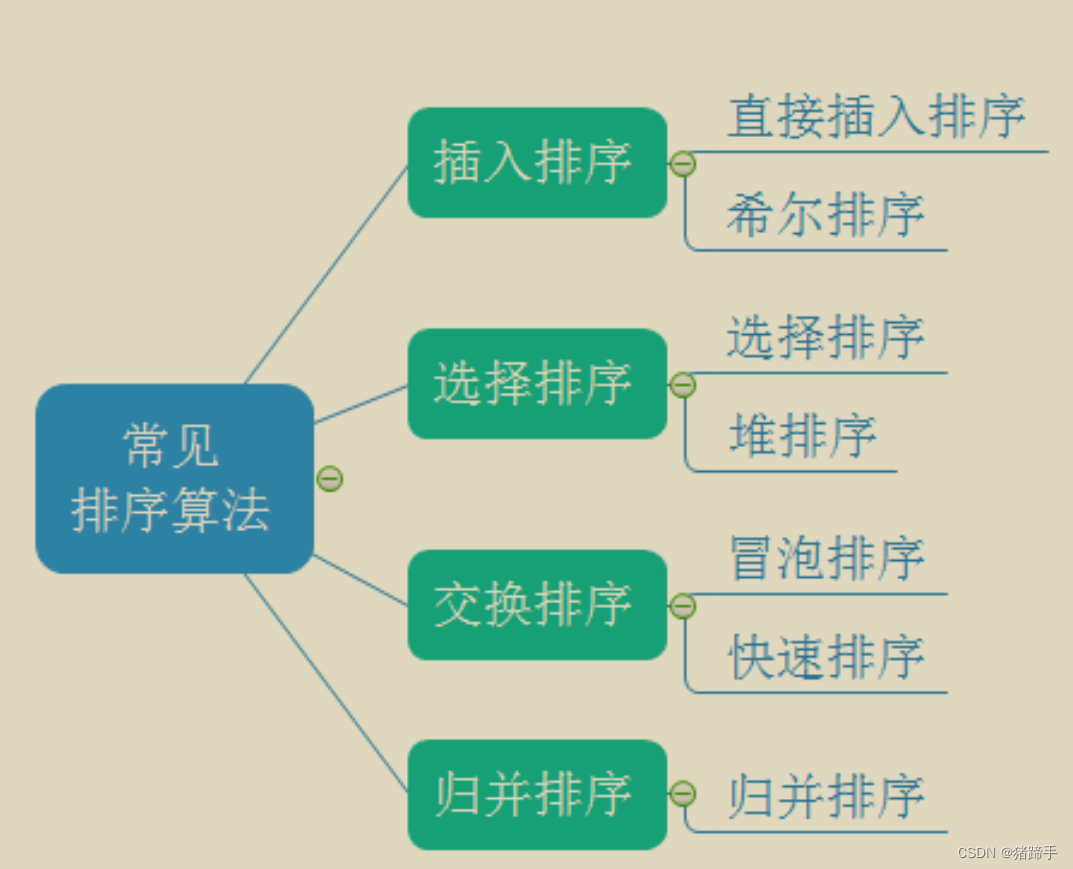
我们就按照这张图来一一实现吧！
一.直接插入排序与希尔排序.
这个是我之前写过的内容了，大家可以通过链接去看看详细内容。
这里就直接赋上代码了
//直接插入排序(升序)
void Insertsort(int* arr, int n)
{
for (int i = 0; i < n - 1; i++)
{
int end = i;
int tmp = arr[end + 1];
while (end >= 0)
{
if (tmp < arr[end])
{
arr[end + 1] = arr[end];
end--;
}
else
{
break;
}
}
arr[end + 1] = tmp;
}
}//希尔排序(升序)
void Shellsort(int* arr, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap / 2;
//gap = gap / 3 + 1;
//先一组组排好
//for (int i = 0; i < gap; i++)
//{
// for (int j = i; j < n - gap; j += gap)
// {
// int end = j;
// int tmp = arr[end + gap];
// while (end >= 0)
// {
// if (tmp < arr[end])
// {
// arr[end + gap] = arr[end];
// end-=gap;
// }
// else
// {
// break;
// }
// }
// arr[end + gap] = tmp;
// }
//}
//多组并排
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = arr[end + gap];
while (end >= 0)
{
if (tmp < arr[end])
{
arr[end + gap] = arr[end];
end-=gap;
}
else
{
break;
}
}
arr[end + gap] = tmp;
}
}
}我们还是分析下他们的时间复杂度吧！
插入排序是通过进行比较来插入的，最坏的情况就是都要比较，所以是O(N^2)，最好情况就是本生就是顺序且有序的。
而希尔排序则不同，大家现在当下只需知道大概在O(1.3N)左右即可
直接插入排序的特性总结：
1. 元素集合越接近有序，直接插入排序算法的时间效率越高
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)，它是一种稳定的排序算法
4. 稳定性：稳定
希尔排序的特性总结：
1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的了，这样就
会很快。这样整体而言，可以达到优化的效果。我们实现后可以进行性能测试的比。
3. 希尔排序的时间复杂度不好计算，因为gap的取值方法很多，导致很难去计算，因此在好些书中给出的希尔排序的时间复杂度都不固定，大家就记为
O(1.3N)
4. 稳定性：不稳定
二.选择排序
选择排序的思想就是：找到最值的两个数，分别放在首尾，然后再选择次一级的，知道排好。是不是非常简单，所以这里我们上代码：
//选择排序(升序)
void Swap(int* p, int* q)
{
int* tmp = *p;
*p = *q;
*q = tmp;
}
void Selectsort(int* arr, int n)
{
int begin = 0;
int end = n - 1;
while (begin < end)
{
int min = begin;
int max = begin;
for (int i = begin + 1; i <= end; i++)
{
if (arr[i] < arr[min])
min = i;
if (arr[i] > arr[max])
max = i;
}
Swap(&arr[begin], &arr[min]);
//注意：这里一定要留意max的值是不是begin位置，如果是，前一个交换会影响到后一个，所以要找到正确的位置
if (max == begin)
max = min;
Swap(&arr[end], &arr[max]);
begin++;
end--;
}
}
直接选择排序的特性总结：
1. 直接选择排序思考非常好理解，但是效率不是很好。实际中很少使用
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)
4. 稳定性：不稳定
三.堆排序
这个之前也实现过了，可以看链接：
这里还是贴下代码：
void Adjustup(int* arr, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (arr[child] > arr[parent])
{
Swap(&arr[child], &arr[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void Adjustdown(int* arr,int parent, int n)
{
int child = parent * 2 + 1;
while (child < n)
{
if (child + 1 < n && arr[child + 1] > arr[child])
{
child++;
}
if (arr[child] > arr[parent])
{
Swap(&arr[child], &arr[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//堆排序
void Heapsort(int* arr, int n)
{
//建大堆
/*for (int i = 1; i < n; i++)
{
Adjustup(arr, i);
}*/
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
Adjustdown(arr,i,n);
}
//堆删除
int end = n - 1;
while (end > 0)
{
Swap(&arr[end], &arr[0]);
Adjustdown(arr,0, end);
end--;
}
}
堆排序的特性总结：
1. 堆排序使用堆来选数，效率就高了很多。
2. 时间复杂度：O(N*logN)
3. 空间复杂度：O(1)
4. 稳定性：不稳定
四.冒泡排序和快速排序
这是一个可以说是最简单的排序了，实现的关键就是想好两层循环的条件就行了，我之前也实现过了，大家可以去之前我的文章看看，这里给大家一个链接吧！
这里直接上代码了，学到这还不会冒泡，建议别在看这个文章了，需要去补就前面的了。
//冒泡排序（升序）
void Bubblesort(int* arr, int n)
{
for (int i = 0; i < n - 1; i++)
{
for (int j = 0; j < n - i - 1; j++)
{
if (arr[j] > arr[j + 1])
Swap(&arr[j], &arr[j + 1]);
}
}
}时间复杂度：O(N^2)
下面开始我们可以说是非常难的部分了----快速排序
快速排序是
Hoare
于
1962
年提出的一种二叉树结构的交换排序方法，其基本思想为：
任取待排序元素序列中
的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右
子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。
我们先直接学hoare版本吧！
注意：hoare的版本是将key取开头的元素
如果我们按照升序排列，我们要先走右边的，这样才能保证相遇的点其值一定比key点的小，原因如下：
相遇分为以下两种情况：
1.左边相遇右边，即右边停止后左边一直走，没有找到比key大的元素直到相遇，而相遇点是右边找小找到的，说明相遇点比key点小（升序）
2.右边相遇左边，即左边停止后右边一直走，没有找到比key小的元素直到相遇，而相遇点是左边找大找到的，说明相遇点比key点大。（降序）
下面我们实现吧！
//快速排序（升序）
void Swap(int* p, int* q)
{
int* tmp = *p;
*p = *q;
*q = tmp;
}
void Quicksort(int* arr, int begin, int end)//注意end到底是啥？如果是元素个数，下面的right要减1，如果是最后一个元素下标，end=right
{
//递归结束条件
if (begin >= end)
return;
int left = begin;
int right = end - 1;
int key = begin;
while (left < right)
{
//先右
while (left < right && arr[right] >= arr[key])//右找小
{
right--;
}
//再左
while (left < right && arr[left] <= arr[key])//左找大
{
left++;
}
Swap(&arr[left], &arr[right]);
}
//相遇点和key交换
Swap(&arr[left], &arr[key]);
//第一次完成
//下面是递归部分
key = left;
Quicksort(arr, 0, key);
Quicksort(arr, key + 1,end);
}这个就是hoare版本了，学到这你可能会问一下问题：
1.为什么左边要找大，右边要找小？
我们如果要排升序，是不是从小到大的顺序，如果交换的左右不是大和小，那么你确定是在排序
2.key为啥就是数组开头元素呢？
这个其实只是hoare版本的key找法，实际上还有其他方法的，下面我们就讲解下其他key找法。
//三数取中法
int Mid(int* arr,int begin, int end)
{
int mid = (begin + end-1) / 2;
if (arr[begin] > arr[end])
{
if (arr[mid] > arr[end])
{
if (arr[begin] > arr[mid])
return mid;
else
return begin;
}
return end;
}
else
{
if (arr[mid] > arr[begin])
{
if (arr[end] > arr[mid])
return mid;
else
return end;
}
return begin;
}
}对于上面的内容要注意我们都是end表示为最后一个元素是第几个元素，而非所在的数组下标。
下面我们将其改成数组下标，再写一遍hoare版本的快排。
//三数取中法
int Mid(int* arr,int begin, int end)
{
int mid = (begin + end) / 2;
if (arr[begin] > arr[end])
{
if (arr[mid] > arr[end])
{
if (arr[begin] > arr[mid])
return mid;
else
return begin;
}
return end;
}
else
{
if (arr[mid] > arr[begin])
{
if (arr[end] > arr[mid])
return mid;
else
return end;
}
return begin;
}
}
void Quicksort(int* arr, int begin, int end)//end表示最后一个元素下标
{
if (begin >= end)
return;
int left = begin;
int right = end;
int key = begin;
while (left < right)
{
while (left < right && arr[right] >= arr[key])
right--;
while (left < right && arr[left] <= arr[key])
left++;
Swap(&arr[left], &arr[right]);
}
Swap(&arr[left], &arr[key]);
key = left;
Quicksort(arr, 0, key - 1);
Quicksort(arr, key + 1, end);
}注意改变之处。
大家可能会发现hoare版本的快排有非常多的点需要注意，于是后人就写出了以下两种不同的写法，对其进行改进。
挖坑法
挖坑法是指先将一个数据储存在数组外面，然后还是右边找小，左边找大，找到就将该位置的数放在原先取出的位置，然后现在的位置即是一个新的坑，一直上述操作直到左右相遇，然后将最开始保存的数据放进相遇位置。
下面我们实现它：
//挖坑法
void partQuicksort(int* arr, int begin, int end)//end表示最后一个元素下标
{
if (begin >= end)
return;
int left = begin;
int right = end;
int key = arr[begin];
int hole = begin;//坑
while (left < right)
{
while (left < right && arr[right] >= key)
right--;
arr[hole] = arr[right];
hole = right;
while (left < right && arr[left] <= key)
left++;
arr[hole] = arr[left];
hole = left;
}
arr[hole] = key;
partQuicksort(arr, begin, hole - 1);
partQuicksort(arr, hole + 1, end);
}
前后指针版本
//前后指针法
void part2Quicksort(int* arr, int begin, int end)//end表示下标
{
if (begin >= end)
return;
int prev = begin;
int cur = begin + 1;
int key = begin;
while (cur <= end)
{
if (arr[cur] < arr[key] && ++prev != cur)
{
Swap(&arr[prev], &arr[cur]);
}
cur++;
}
Swap(&arr[prev], &arr[key]);
key = prev;
part2Quicksort(arr, 0, key - 1);
part2Quicksort(arr, key + 1, end);
}对于快排还可以优化，例如：我们这里实现时发现，大部分的递归都是在元素非常小的时候，所以如果我们可以将这部分改成其他排序，是不是可以节省一部分空间。
我们以hoare版本为例：
void Quicksort2(int* arr, int begin, int end)//end表示最后一个元素下标
{
if (begin >= end)
return;
//如果元素小于等于10，利用其他排序，这里我们选择插入排序
if (end - begin + 1 <= 10)
{
Insertsort(arr+begin, end - begin + 1);//注意这里数组也要变
}
else
{
int left = begin;
int right = end;
int key = begin;
while (left < right)
{
while (left < right && arr[right] >= arr[key])
right--;
while (left < right && arr[left] <= arr[key])
left++;
Swap(&arr[left], &arr[right]);
}
Swap(&arr[left], &arr[key]);
key = left;
Quicksort(arr, 0, key - 1);
Quicksort(arr, key + 1, end);
}
}快排学到现在了，大家是不是觉得自己行了？？？现在我请你实现快排的非递归，请问你如何实现呢？
//快排非递归
int Quicksort3(int* arr, int begin, int end)
{
//我们这里就用挖坑法实现
int hole = begin;
int key = arr[begin];
while (begin < end)
{
while (begin < end && arr[end] >= key)
end--;
arr[hole] = arr[end];
hole = end;
while (begin < end && arr[begin] <= key)
begin++;
arr[hole] = arr[begin];
hole = begin;
}
arr[hole] = key;
return hole;
}
void QuicksortNone(int* arr, int begin, int end)
{
SS s1;
StackInit(&s1);
StackPush(&s1,begin);
StackPush(&s1, end);
while (!StackEmpty(&s1))
{
int right = StackTop(&s1);
StackPop(&s1);
int left = StackTop(&s1);
StackPop(&s1);
int key = Quicksort3(arr, left, right);
if (left < key - 1)
{
StackPush(&s1, left);
StackPush(&s1,key-1);
}
if (right > key + 1)
{
StackPush(&s1,key+1);
StackPush(&s1,right);
}
}
StackDestory(&s1);
}
快速排序的特性总结：
1. 快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序
2. 时间复杂度：O(N*logN)
3. 空间复杂度：O(logN)
4. 稳定性：不稳定
五.归并排序
基本思想：
归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。
//归并排序
void _Mergesort(int* arr, int begin, int end, int* tmp)
{
if (begin >= end)
return;
//先递归
int mid = (begin + end) / 2;
_Mergesort(arr, begin, mid, tmp);
_Mergesort(arr, mid + 1, end,tmp);
//并
int begin1 = begin;
int end1 = mid;
int begin2 = mid + 1;
int end2 = end;
int i = begin;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
{
tmp[i++] = arr[begin1++];
}
else
{
tmp[i++] = arr[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = arr[begin2++];
}
memcpy(arr + begin, tmp + begin, (end - begin + 1)*sizeof(int));
}
void MergeSort(int* arr, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
//检查
if (tmp == NULL)
{
perror(tmp);
return;
}
_Mergesort(arr, 0, n-1, tmp);
free(tmp);
tmp = NULL;
}当然，归并排序也可以非递归实现，由于实现过于复杂，所以我们现在就先不是实现了，以后我们会讲的。
大家加油！
文章来源:https://blog.csdn.net/2301_79813267/article/details/135328821
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码（1）
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- C#设计模式教程（7）：适配器模式
- 【剑指offer】替换空格
- 基于模糊PID控制器的风力温度控制系统simulink建模与仿真
- 程序媛的mac修炼手册-- 终端shell的驾驭 zsh vs bash
- 鸿蒙APP的设备适配
- 知识笔记（六十四）———Vue 3中toRaw和markRaw的使用
- 车载蓝牙物联网解决方案
- JavaScript 对象及初始面向对象【万字长篇超宝典！】
- C++学习笔记（二十二）
- 力扣题目学习笔记(OC + Swift)21. 合并两个有序链表