day18 找树左下角的值 路径总和 路径总和Ⅱ 从中序与后序遍历序列构造二叉树 从前序与中序遍历序列构造二叉树

题目1：513 找树左下角的值

题目链接：513 找树左下角的值

题意

找出二叉树的最底层? 最左边节点的值? ? ?(假设二叉树中至少有1个节点)

最底层节点确保是深度最大的叶子节点，最左边的节点却不一定是左孩子

递归遍历

深度最大的叶子节点最左侧的值，使用前序（中左右）中序（左中右）后序（左右中）遍历均可，因为都是先遍历左，后遍历右，这样确保先遍历左节点，如果左节点满足，就会直接放入result中，如果没有左节点，才会遍历同层的右节点? 这样保证遍历的是二叉树的深度最大的叶子节点的最左边的值

递归三部曲

1）确定递归函数的参数和返回值

2）确定终止条件

3）确定单层递归逻辑

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxdepth = INT_MIN;//记录最大深度
    int result = 0;//记录最大深度对应的节点数值
    void traversal(TreeNode* node,int depth){
        //终止条件  叶子节点
        if(node->left==NULL && node->right==NULL){
            if(maxdepth < depth){
                maxdepth = depth;
                result = node->val;
            }
        }
        //单层递归逻辑
        if(node->left){
            depth++;
            traversal(node->left,depth);
            depth--;//回溯
        }
        if(node->right){
            depth++;
            traversal(node->right,depth);
            depth--;//回溯
        }
    }
    int findBottomLeftValue(TreeNode* root) {
        int depth = 0;
        traversal(root,depth);
        return result; 
    }
};

逻辑

如果右节点的值大于本层左节点的值，会改变result吗？

Answer：并不会

层序遍历

记录最后一层遍历到的第一个节点的值就可

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int findBottomLeftValue(TreeNode* root) {
        queue<TreeNode*> que;
        int result = 0;
        if(root!=NULL) que.push(root);
        while(!que.empty()){
            int size = que.size();
            for(int i=0;i<size;i++){
                TreeNode* node = que.front();
                que.pop();
                if(i==0) result = node->val;//记录每一层的第一个节点的值 直到更新到最后一层
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
        }
        return result;
    }
};

题目2：112 路径总和

题目链接：112 路径总和

题意

判断是否存在：根节点到叶子节点的路径上所有节点值相加等于目标和targetsum

如果存在，返回true，如果不存在，返回false

递归

前序遍历，中序遍历，后序遍历均可，因为没有中节点的处理逻辑

递归三部曲：

1）确定递归函数的返回值和参数? ?只要有1条路径就行，返回true? 所以递归函数需要返回值

2）确定终止条件

3）确定单层递归逻辑

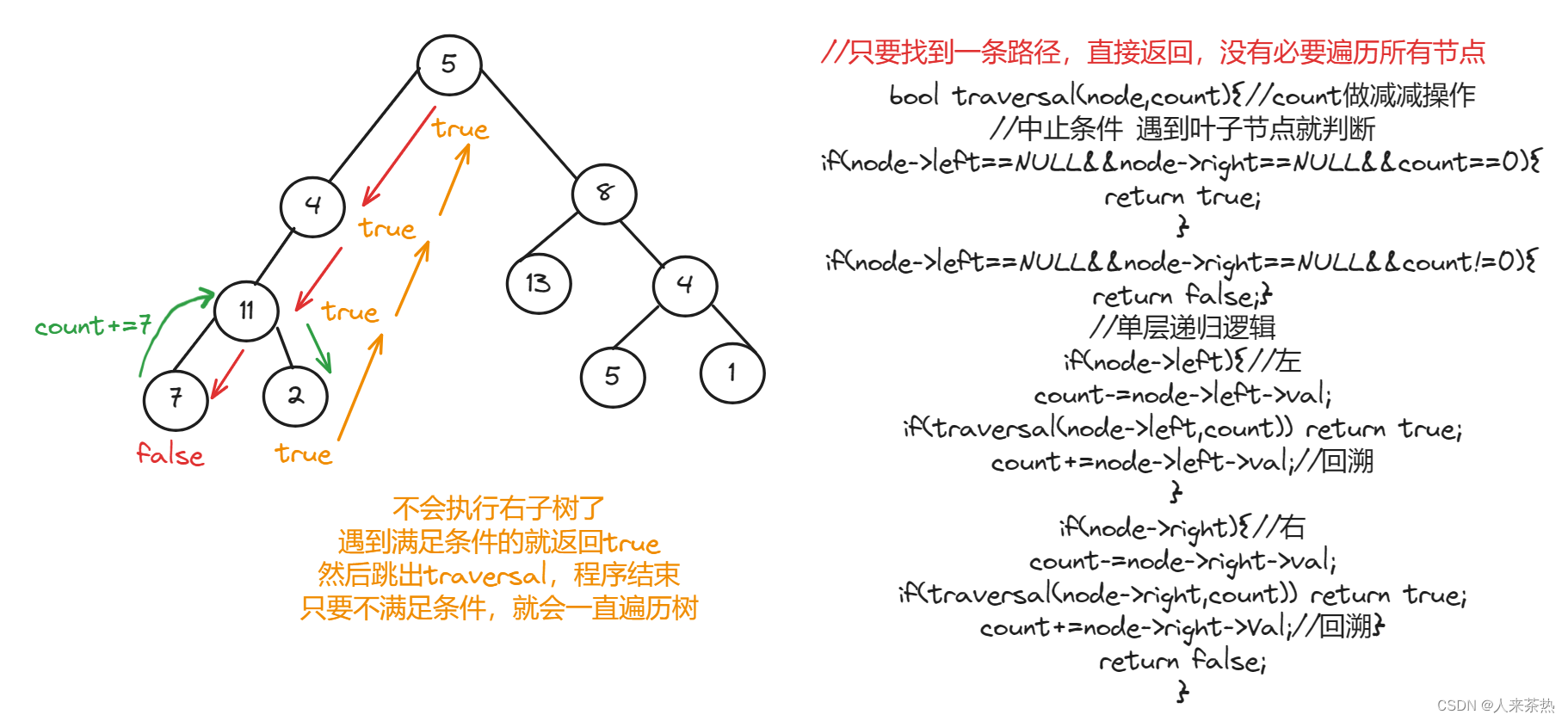
代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool traversal(TreeNode* node,int count){
        //终止条件  遇到叶子节点就判断一下
        if(node->left==NULL && node->right==NULL && count==0) return true;
        if(node->left==NULL && node->right==NULL && count!=0) return false;
        //单层递归逻辑
        if(node->left){
            count -= node->left->val;
            if(traversal(node->left,count)) return true;
            count += node->left->val;
        }
        if(node->right){
            count -= node->right->val;
            if(traversal(node->right,count)) return true;
            count += node->right->val;
        }
        return false;
    }
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(root==NULL) return false;
        return traversal(root,targetSum-root->val);
    }
};

迭代遍历

使用栈的方法代替递归遍历? 栈中放入两个值：当前节点? 当前总和

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(root==NULL) return false;
        stack<pair<TreeNode*,int>> st;
        st.push(pair<TreeNode*,int>(root,root->val));//st的第二个位置处的整数做加加操作
        while(!st.empty()){
            pair<TreeNode*,int> node = st.top();
            st.pop();
            if(node.first->left==NULL && node.first->right==NULL && node.second==targetSum) return true;
            if(node.first->right) st.push(pair<TreeNode*,int>(node.first->right,node.second+node.first->right->val));//左
            if(node.first->left) st.push(pair<TreeNode*,int>(node.first->left,node.second+node.first->left->val));//右
        }
        return false;
    }
};

题目3：113 路径总和Ⅱ

题目链接：路径总和Ⅱ

题意

找出所有根节点到叶子节点的路径总和等于targetsum的路径

递归遍历

要遍历所有的节点，所以递归函数不需要返回值

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> path;
    vector<vector<int>> result;
    void traversal(TreeNode* node,int count){
        //终止条件
        if(node->left==NULL && node->right==NULL && count==0){
            result.push_back(path);
            return;
        }
        //单层递归逻辑
        if(node->left){
            path.push_back(node->left->val);
            count -= node->left->val;
            traversal(node->left,count);
            count += node->left->val;
            path.pop_back();
        }
        if(node->right){
            path.push_back(node->right->val);
            count -= node->right->val;
            traversal(node->right,count);
            count += node->right->val;
            path.pop_back();
        }
    }
    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        if(root==NULL) return result;
        path.push_back(root->val);
        traversal(root,targetSum-root->val);
        return result;
    }
};

迭代遍历较为复杂

题目4：106 从中序与后序遍历序列二叉构造树

题目链接：106 从中序遍历与后序遍历序列构造二叉树

题意

根据中序遍历数组inorder和后序遍历数组postorder构造二叉树

递归

递归三部曲：

1）确定递归函数的参数和返回值

2）确定终止条件

3）确定单层递归逻辑

数组

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        //终止条件
        if(postorder.size()==0) return NULL;
        //单层递归逻辑
        //中节点
        int rootvalue = postorder[postorder.size()-1];
        TreeNode* root = new TreeNode(rootvalue);
        if(postorder.size()==1) return root;//叶子节点
        //寻找中序数组的切割点index
        int index;
        for(index=0;index<inorder.size();index++){
            if(inorder[index]==rootvalue){
                break;
            }
        }

        //切割中序数组(左中右)  左闭右开  循环不变量
        //中序左
        vector<int> inorderleft(inorder.begin(),inorder.begin()+index);
        //中序右  //注意抛除掉中节点
        vector<int> inorderright(inorder.begin()+index+1,inorder.end());
       
        //切割后序数组(左右中)
        //去除掉中节点
        postorder.resize(postorder.size()-1);
        //后序左
        vector<int> postorderleft(postorder.begin(),postorder.begin()+inorderleft.size());
        //后序右
        vector<int> postorderright(postorder.begin()+inorderleft.size(),postorder.end());
        
        //左子树
        root->left = buildTree(inorderleft,postorderleft);
        //右子树
        root->right = buildTree(inorderright,postorderright);
        return root;
    }
};

下标（节省空间复杂度）

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* traversal(vector<int>& inorder,int inorderbegin,int inorderend,vector<int>& postorder,int postorderbegin,int postorderend){
        //终止条件
        if(postorderbegin == postorderend) return NULL;
        //单层递归逻辑
        //中节点
        int rootvalue = postorder[postorderend-1];
        TreeNode* root = new TreeNode(rootvalue);
        if(postorderend-postorderbegin==1) return root;
        //中序数组切割点
        int index;
        for(index=inorderbegin;index<inorderend;index++){
            if(inorder[index]==rootvalue){
                break;
            }
        }
        //切割中序数组（左中右）  左闭右开
        //中序左
        int inorderleftbegin = inorderbegin;
        int inorderleftend = index;//注意使用的是索引的方法，所以这里直接使用索引
        //中序右  抛除掉中节点
        int inorderrightbegin = index + 1;
        int inorderrightend = inorderend;
        //切割后序数组（左右中）  左闭右开
        //后序左
        int postorderleftbegin = postorderbegin;
        int postorderleftend = postorderbegin + (inorderleftend - inorderleftbegin);//由于后序是通过中序左的的大小得到的，所以前面要加上postorderbegin
        //后序右  抛除掉中节点
        int postorderrightbegin= postorderbegin + (inorderleftend - inorderleftbegin);
        int postorderrightend = postorderend - 1;
        // cout<<"inorderleft:";//中序左
        // for(int i=inorderleftbegin;i<inorderleftend;i++){
        //     cout<<inorder[i]<<" ";
        // }
        // cout<<endl;
        // cout<<"inorderright:";//中序右
        // for(int j=inorderrightbegin;j<inorderrightend;j++){
        //     cout<<inorder[j]<<" ";
        // }
        // cout<<endl;
        // cout<<"postorderleft:";//后序左
        // for(int i=postorderleftbegin;i<postorderleftend;i++){
        //     cout<<postorder[i]<<" ";
        // }
        // cout<<endl;
        // cout<<"postorderright:";//后序右
        // for(int i=postorderrightbegin;i<postorderrightend;i++){
        //     cout<<postorder[i]<<" ";
        // }
        // cout<<endl;
        root->left = traversal(inorder,inorderleftbegin,inorderleftend,postorder,postorderleftbegin,postorderleftend);
        root->right = traversal(inorder,inorderrightbegin,inorderrightend,postorder,postorderrightbegin,postorderrightend);
        return root;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        //终止条件
        if(postorder.size()==0) return NULL;
        return traversal(inorder,0,inorder.size(),postorder,0,postorder.size());  //左闭右开
    }
};

题目5：105 从前序与中序遍历序列构造二叉树

题目链接：105 从前序与中序遍历序列构造二叉树

题意

根据前序遍历数组preorder和中序遍历数组inorder构造二叉树

递归

数组

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        //终止条件
        //空节点
        if(preorder.size()==0) return NULL;
        //单层递归逻辑
        //中节点
        int rootvalue = preorder[0];
        TreeNode* root = new TreeNode(rootvalue);
        if(preorder.size()==1) return root;//叶子节点
        //中序数组切割点
        int index;
        for(index=0;index<inorder.size();index++){
            if(inorder[index]==rootvalue){
                break;
            }
        }
        //切割中序数组(左中右)   左闭右开
        //中序左
        vector<int> inorderleft(inorder.begin(),inorder.begin()+index);
        //中序右   抛除掉中节点元素
        vector<int> inorderright(inorder.begin()+index+1,inorder.end());
        //切割前序数组(中左右)  左闭右开
        //抛除掉中节点元素
        //前序左
        vector<int> preorderleft(preorder.begin()+1,preorder.begin()+1+inorderleft.size());
        //前序右
        vector<int> preorderright(preorder.begin()+1+inorderleft.size(),preorder.end());
        root->left = buildTree(preorderleft,inorderleft);
        root->right = buildTree(preorderright,inorderright);
        return root;
    }
};

下标

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* traversal(vector<int>& preorder, int preorderbegin, int preorderend, vector<int>& inorder,int inorderbegin, int inorderend){
        //终止条件
        if(preorderend-preorderbegin==0) return NULL;
        //单层递归逻辑
        //中节点
        int rootvalue = preorder[preorderbegin];
        TreeNode* root = new TreeNode(rootvalue);
        //叶子节点
        if(preorderend-preorderbegin==1) return root;
        //中序数组切割点
        int index;
        for(index=0;index<inorderend;index++){
            if(inorder[index]==rootvalue){
                break;
            }
        }
        //切割中序数组 左中右
        //中序左
        int inorderleftbegin = inorderbegin;
        int inorderleftend = index;
        //中序右  抛除中节点index
        int inorderrightbegin = index + 1;
        int inorderrightend = inorderend;
        //切割前序数组  中左右
        //前序左  抛除中节点preorderbegin
        int preorderleftbegin = preorderbegin + 1;
        int preorderleftend = preorderbegin + 1 + (index - inorderbegin);
        //前序右  
        int preorderrightbegin = preorderbegin + 1 + (index - inorderbegin);
        int preorderrightend = preorderend;
        root->left = traversal(preorder,preorderleftbegin,preorderleftend,inorder,inorderleftbegin,inorderleftend);
        root->right = traversal(preorder,preorderrightbegin,preorderrightend,inorder,inorderrightbegin,inorderrightend);
        return root;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if(preorder.size()==0) return NULL;
        return traversal(preorder,0,preorder.size(),inorder,0,inorder.size());
    }
};