快慢指针-Floyd判圈算法

对于环形链表是否存在环的做法，普通算法可以通过额外Hash数组来存储链表元素，直到Hash数组中出现重复元素。时间复杂度O(n)，空间复杂度O(n)

Floyd判圈算法通过利用快慢指针的移动来实现，时间复杂度O（n），空间复杂度O（1）

一、环形链表

这个不需要过过多的介绍，环形链表就是存在一个节点被2个节点指向，形成了一个闭环。

需要注意的是，一个节点可以被两个节点指向，但是不可能一个节点指向多个节点，所以不会出现一下情况：

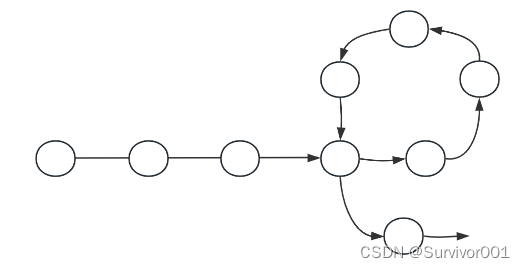
二、算法结论

存在不同速度的快慢指针（slow & fast），慢指针每周期移动1个节点，快指针每周期移动2节点

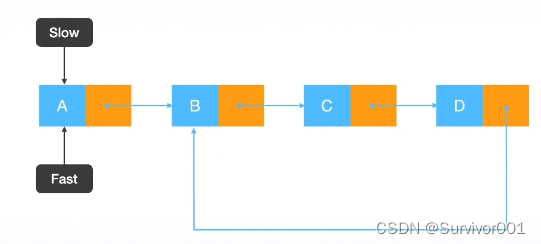
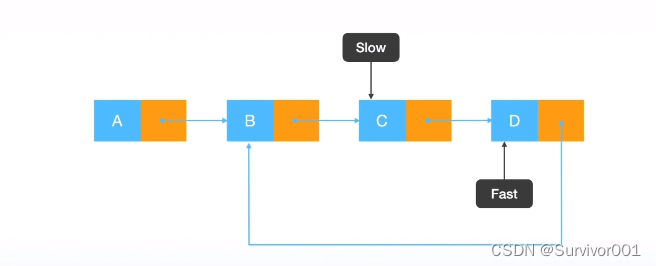
1、因为快指针比慢指针速度快，所以如果链表中不存在环时，快慢指针永远不得相遇，直到Fast移动到尾部结束，时间复杂度O（n），因为Fast指针速度是Slow指针两倍，所以当Fast指针到达尾部时，Slow指针走了一半，即S指向中间值。

2、如果存在环，Fast先进入到环内，并开始做绕环移动，Slow和Fast在环内经过n次移动后，必然会相遇

3、快慢指针在环内第一次相遇后，将其中一个指针重置到head位，当他们再次相遇后指向的节点为入环节点

三、算法证明

1、每次循环，为什么快慢指针一定要快1步，是否可以前进更多？（Slow前进1格，Fast前进2格）

这是因为快慢指针如果相距更多的步，可能存在环内永远不会相遇的情况，比如慢指针前进1格，快指针前进4格时，如下

因为环节点数据量为3个，所以对于Fast指针来说每次循环等于前进1格，而慢指针也前进1格，所以两者永远不能相遇。

因此想要快慢指针在环内能必然或者更快的相遇，那需要他们每次循环后，距离-1，直到相遇。F指针比S指针快1步，可以更好的保障其在环境一定能够相遇，或者更早的相遇。

2、为什么快慢指针在环内一定会相遇？

假如快慢指针此时都在环内，他们相距距离为N，因为环是无限循环的，假设次数S指针在F指针前，即S-F=N

?因为F指针比S指针快1步，所以进行1次移动后：

S+1-(F+2) = S-F -1 = N-1 ，即执行一次后两者的距离-1，因此在n次循环后，必然会出现相遇。

此时如果将设F指针速度为vf， 慢指针速度为vs，同时要确保一定相遇满足N-1，则：

S+vs -(F +vf) = N-1? ?

? --> S-F + vs-vf = n-1??

? --> vs - vf = 1，即相差1步

同时N为两者的距离，肯定是小于环的长度的，所以在S指针进环后，第1圈内一定会相遇

结论：

首先F指针每次比S指针快1步，可以确保在环中一定可以相遇，如果快更多，则不能保证或需要更多的循环。

3、入口节点结论证明

上面已经证明了F\S在环中一定是能够相遇的，且S进环后，第一圈一定会相遇，那么假设F\S

在P点相遇

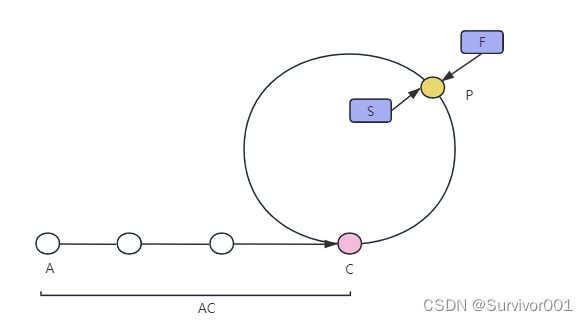
因为F比S快1步，所以F在环内已经跑了1圈了

因此F行驶距离：AC + 2CP + PC

S行驶距离：AC + CP

因为F速度为S的两倍，因此?AC + 2CP + PC = 2（AC + CP）得出 AC = PC

即：在第一次相遇时，PC和AC的长度是一样的，因此此时将任意节点重置到A位，并两者均以相同的速度前进，必然会在C点相遇，因此C点为入口点。

4、原理理解了算法就比较简单了

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public int hasCycle(ListNode head) {
        if(head == null){
           return -1;
        }
         ListNode fast = head;
         ListNode slow = head;
         // 第一次相遇
         while(true){
             if(slow.next == null  || fast.next == null ){
                return false;
             }
             fast = fast.next.next;
             slow = slow.next;
             if(fast == slow){
                  break;
             }
             
         } 
         // 第二次相遇 
         while(fast!=slow){
             fast = fast.next;
             slow = slow.next;
             if(fast == slow){
                  return fast ;
             }
             
         } 
    }
}