2023,TEVC,A Competitive and Cooperative Swarm Optimizer for Constrained MOP

Abstract
通过元启发式方法求解多目标优化问题( MOPs )得到了广泛的关注。在经典变异算子的基础上,发展了几种改进的变异算子,以及多目标优化进化算法。在这些算子中,竞争群优化算法(CSO)表现出良好的性能。然而,在处理目标空间较大或不可行区域复杂的约束多目标优化问题时遇到了困难。在本文中,提出了一种竞争和合作的群优化算法,其中包含两种粒子更新策略:1) CSO提供更快的收敛速度以加速Pareto前沿的逼近;2)合作群优化算法提出了一种相互学习策略以增强跳出局部可行区域或局部最优的能力。我们还提出了一种新的CMOPs算法。在4个包含47个实例的基准测试集上的实验结果表明,与其他先进方法相比,我们的方法具有更好的性能。此外,其在大规模CMOPs上的有效性也得到了验证。
I. INTRODUCTION
多目标优化问题(MOPs)是指包含两个或多个相互冲突目标的优化问题[1]。MOPs广泛存在于现实世界的应用中[2],[3]。由于现实世界中的许多优化问题都包含各种约束,约束多目标优化 (CMOPs) 普遍存在,如在多技能资源约束的项目调度[4],基数约束的投资组合优化[5],以及可靠性约束的多目标测试资源分配[6]中。
通过进化算法(EAs)求解CMOPs是常见的。基于进化算子的CMOPs [7],[8]已经开发了各种约束多目标进化算法(CMOEAs)。一些研究人员提出了基于遗传算法(GA)、差分进化算法(DE)和粒子群算法(PSO)的增强算子,以提高在处理CMOPs时的搜索能力[9],[10],[11],[12]。在这些改进算子中,基于PSO的竞争群优化算法(CSO) [10]对多目标优化问题具有较快的收敛速度。然后,Tian等人[12]提出了一种改进的CSO ( iCSO ),以进一步提高其在大规模MOPs (LSMOPs)上的性能。然而,CSO和 iCSO 在处理目标空间较大或不可行区域复杂的CMOPs时遇到了困难。
1) loser 粒子在向 winner 粒子学习的过程中,可能会出现运动速度过慢的情况。这样,在求解目标空间较大的CMOPs时,CSO和iCSO的收敛效率就会退化。
2) 对于具有复杂不可行域的CMOPs,CSO和iCSO容易陷入局部最优或局部可行域。
为了弥补这些缺陷,本文提出了一种新的CMOPs求解算法CMOCSO。具体来说,本文的主要贡献可以概括如下:
1) 提出了一种新的群优化算法:竞争合作型群优化算法(Competitive and Cooperative Swarm Optimization,CCSO),它包含一个CSO和一个合作型群优化算法。CSO加速了收敛,以解决具有大目标空间的CMOPs。此外,协作群体优化器提出了一种相互学习策略,以增强CSO跳出局部最优或局部可行域的能力。
2) 新的CMOEA:设计了一种协同进化策略。CSO 使用一个群体,基于约束松弛技术搜索约束帕累托前沿(CPF)。另一种用于协同群优化器,它忽略约束条件,进行帕累托前沿(PF)搜索。此外,基于约束优先技术,使用存档群来维护一个可行解集,并不断促进其收敛性和多样性,作为最终的解集。在CCSO和协同进化策略的基础上,提出了CMOCSO。
在4个CMOP基准测试集共47个算例上的结果证明了CMOCSO相对于6个最先进的CMOEA的优越性。此外,CMOCSO在24个LSCMOPs上进行了评估,共72个实例。结果表明,CMOCSO也可以获得比其他最先进的大规模CMOEA更好的性能。
本文的其余部分组织如下。第二节介绍了本文的研究背景和相关工作。第三节详细介绍了CCSO和CMOCSO的提出。第四节给出了结果和分析。最后,在第五章中总结了本文的结论,并对未来的工作进行了展望。
II. RELATED WORK
A. Related Constraint-Handling Techniques
有两种相关的约束处理技术(CHT)。
1)约束占优原则: Deb等[ 13 ]在NSGA-II中提出了约束占优原则( CDP )。给定两个解x和y,如果下列条件之一成立,则称 x 约束支配 y (记为
x
?
c
y
\mathbf{x}\prec_{c}\mathbf{y}
x?c?y):
1
)
?
(
x
)
<
?
(
y
)
;
2
)
?
(
x
)
=
?
(
y
)
and?x
?
y
\begin{array}{rl}1)&\phi(\mathbf{x})<\phi(\mathbf{y});\\2)&\phi(\mathbf{x})=\phi(\mathbf{y})\text{and x}\prec\mathbf{y}\end{array}
1)2)??(x)<?(y);?(x)=?(y)and?x?y?
其中,x?y 表示 x Pareto 支配 y,且满足以下两个条件。
1
)
?
i
∈
{
1
,
…
,
m
}
,
f
i
(
x
)
≤
f
i
(
y
)
.
2
)
?
i
∈
{
1
,
…
,
m
}
,
f
i
(
x
)
<
f
i
(
y
)
.
\begin{matrix}1)&\forall i\in\{1,\ldots,m\},f_i(\mathbf{x})\leq f_i(\mathbf{y}).\\2)&\exists i\in\{1,\ldots,m\},f_i(\mathbf{x})<f_i(\mathbf{y}).\end{matrix}
1)2)??i∈{1,…,m},fi?(x)≤fi?(y).?i∈{1,…,m},fi?(x)<fi?(y).?
由于CDP操作简单,已被广泛应用于各类CMOEA中。然而,正如文献[14]和文献[15]所指出的,对可行解的偏好性使得算法容易陷入局部可行域,特别是当可行域不连续或存在内、外层时。
2) ε -约束技术: 为了克服CDP的局限性,Takahama and Sakathe [16]设计了ε-约束技术。在松弛因子ε的作用下,一些不可行解有可能存活到下一代。因此,增强了跳出局部可行域的能力。给定两个解 x x x 和 y y y,如果下列条件之一成立,则 x ε-约束支配 y (记为 x ? ε y \mathbf{x}\prec_{\varepsilon}\mathbf{y} x?ε?y)。
1 ) ? ? ( x ) < ε ??? & ?? ? ( y ) < ε ? a n d ? x < y . 2 ) ? ? ( x ) = ? ( y ) = ε ? a n d ? x < y . 3 ) ? ? ( x ) > ε ??? & ?? ? ( y ) > ε ? a n d ? ? ( x ) < ? ( y ) . \begin{array}{ll}\mathrm{1)~\phi(x)<\varepsilon~~~\&~~\phi(y)<\varepsilon~and~x<y.}\\\mathrm{2)~\phi(x)=\phi(y)=\varepsilon~and~x<y.}\\\mathrm{3)~\phi(x)>\varepsilon~~~\&~~\phi(y)>\varepsilon~and~\phi(x)<\phi(y).}\end{array} 1)??(x)<ε???&???(y)<ε?and?x<y.2)??(x)=?(y)=ε?and?x<y.3)??(x)>ε???&???(y)>ε?and??(x)<?(y).?
ε-约束技术在CMOEAs [17],[18]中也得到了广泛的应用。Fan等人在LIR-CMOP [19]和PPS [20]中设计了两种改进的ε更新策略。这两种策略分别表示为(1)式和(2)式
ε ( k ) = { ? k ( x θ ) , i f ? k = 0 ( 1 ? τ ) ε ( k ? 1 ) , i f ? r k < α and?k<T c ( 1 + τ ) ? max ? , i f ? r k ≥ α and?k<T c 0 , i f ? k ≥ T c (1) \left.\varepsilon(k)=\left\{\begin{array}{ll}\phi^k(\mathbf{x}^\theta),&\mathrm{if~}k=0\\(1-\tau)\varepsilon(k-1),&\mathrm{if~}r_k<\alpha\text{and k<T}_c\\(1+\tau)\phi_{\max},&\mathrm{if~}r_k\geq\alpha\text{and k<T}_c\\0,&\mathrm{if~}k\geq T_c\end{array}\right.\right.\quad\text{(1)} ε(k)=? ? ???k(xθ),(1?τ)ε(k?1),(1+τ)?max?,0,?if?k=0if?rk?<αand?k<Tc?if?rk?≥αand?k<Tc?if?k≥Tc??(1)
其中, ? k ( x θ ) \phi^k(\mathbf{x}^\theta) ?k(xθ) 是初始种群中具有最大 CV 的前 θ % \theta\% θ% 个体的总体 CV; r k r_k rk? 是可行比率; k k k 表示第 k k k 代; τ \tau τ 和 α \alpha α 是两个控制参数; ? m a x \phi_\mathrm{max} ?max? 是迄今为止发现的最大 CV, T c T_c Tc? 是控制迭代
ε ( k ) = { ( 1 ? τ ) ε ( k ? 1 ) , if??? r k < α ε ( 0 ) ( 1 ? k T c ) c p , if??? r k ≥ α ( 2 ) \left.\varepsilon(k)=\left\{\begin{array}{ll}(1-\tau)\varepsilon(k-1),&\text{if}~~~r_k<\alpha\\\varepsilon(0)\Big(1-\frac{k}{T_c}\Big)^{cp},&\text{if}~~~r_k\geq\alpha\end{array}\right.\right.\quad(2) ε(k)={(1?τ)ε(k?1),ε(0)(1?Tc?k?)cp,?if???rk?<αif???rk?≥α?(2)
其中,cp用于控制在 r k ≥ α r_k≥α rk?≥α的情况下减少约束松弛的速度,ε(0) 为 push search 结束时的最大CV。
B. Existing PSO-Based MOEAs
PSO [21]是求解优化问题最流行的元启发式算法之一。自第一个多目标粒子群优化算法提出以来[ 22 ],人们对粒子群优化算法处理多目标优化问题进行了大量研究。现有的基于PSO的MOEAs大致可以分为以下三类。
第一类在求解多目标优化问题时,倾向于设计新的方法来确定pbest和gbest。例如,在MOPSO [22],SMPSO [23]和NMPSO [24]中,非支配解存储在外部存档中;然后从外部存档中选择gbest。在MO-Ring-PSOSCD [11]中,gbest的位置是由环形拓扑结构决定的粒子邻域内的最佳粒子。
第二类通过修改速度更新策略来改进粒子更新策略,以适应多目标优化问题。例如,pccsAMOPSO [25]和MO-TRIBES [ 26 ]提出了速度更新中的参数自适应策略。在dMOPSO [27]中,如果得到的位置在决策空间之外,则将每个速度乘以- 1反向。在SMPSO [23]中,每个速度更新后乘以一个收缩因子,然后根据决策变量的边界值对其进行约束。
第三类是对MOPs采用协同或并行化技术。在CVEPSO [28]中,合作原则被嵌入到向量评估的PSO [ 29 ]中,得到的方法优于先前基于PSO的MOEAs。SMPSO [23]在CCSMPSO [30]中通过合作协同进化范式进行并行化。
C. Competitive Swarm Optimizer and Discussion
为了替代原始的PSO框架,一种新的基于成对竞争策略的群优化算法被开发出来,称为CSO [31]。与传统PSO不同,CSO不确定pbest或gbest。相反,CSO将粒子群分为 winner group and a loser group。然后,每个 loser 向 winner 学习以提高自己。
最近,CSO在求解LSMOPs方面受到了更多的关注[10],[12],[32],[33]。CSO的核心思想是从 loser particle 到 winner particle 的两两竞争和学习策略。通过竞争机制,验证了CSO比PSO对LSMOPs具有更快的收敛速度[10]。Tian等[12]提出iCSO方法,通过调整CSO的更新策略来进一步提高其性能。具体而言,loser 的粒子更新策略
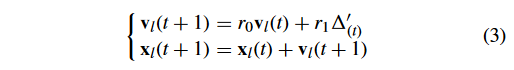
式中:t 为迭代数索引; v l v_l vl? 和 x l x_l xl? 分别表示 loser 粒子的速度和位置;根据文献[10]和文献[12], r 0 r_0 r0? 和 r 1 r_1 r1? 为 [0,1] 中的均匀随机分布值;而 Δ ( t ) ′ \Delta^{\prime}_{(t)} Δ(t)′?是由 loser 到 winner 的向量,可以公式化为:
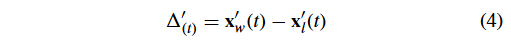
x w ′ ( t ) 、 x l ′ ( t ) x_w^{\prime}(t) 、x_l^{\prime}(t) xw′?(t)、xl′?(t) 的计算公式为:
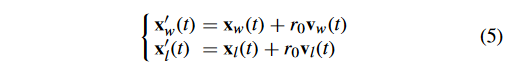
式中: v w v_w vw? 和 x w x_w xw? 分别表示 winner particle 的速度和位置。
正如Tian等人[34]指出的,并在实验实践中得到验证[12],[33],基于粒子群的PSO,CSO和iCSO具有较高的收敛速度和较强的搜索能力。由于约束条件的存在,求解CMOPs需要优化器在收敛到CPF的同时对可行域具有较强的搜索能力。因此,将该算子扩展到CMOPs是很有前途的。然而,iCSO由于自身的特点和局限性,并不能很好地处理CMOPs。为了更好地理解这些特征和限制,图1展示了不同情况下的搜索行为,其中 x b ∈ C P S x_b∈CPS xb?∈CPS 是一个Pareto最优解。
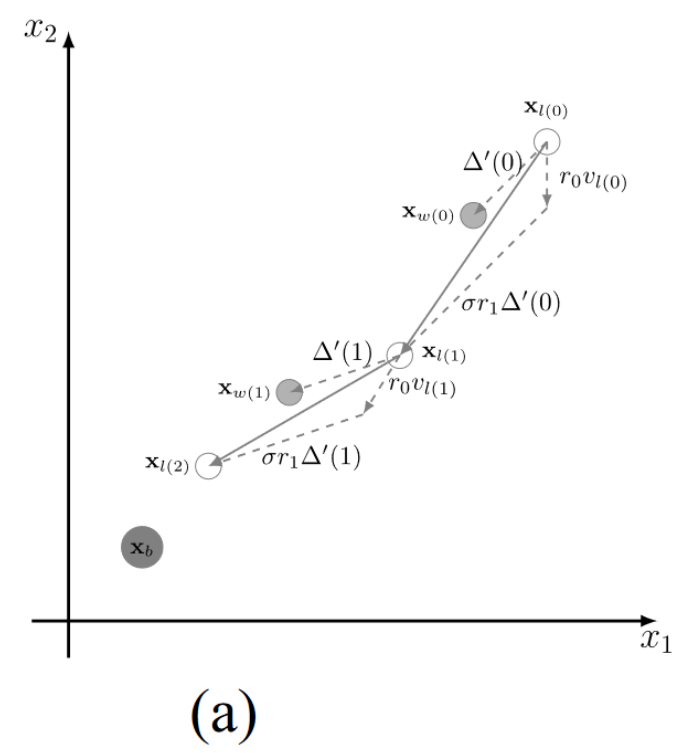
如图 1(a) 所示,通过向 x w ( 0 ) \mathbf{x}_{w}(0) xw?(0) 学习, x l ( 0 ) x_l(0) xl?(0) 移动到 x l ( 1 ) _l(1) l?(1);然后,通过向 x w ( 1 ) \mathbf{x}_{w}(1) xw?(1) 学习, x l ( 1 ) x_l(1) xl?(1) 移动到 x l ( 2 ) x_l(2) xl?(2)。这样,粒子可以通过向更好的粒子(即winner particle)学习,逐渐逼近 x b x_b xb?,然而,如图所示, r 1 Δ ′ r_1\Delta^{\prime} r1?Δ′ 总是小于 Δ ′ \Delta^{\prime} Δ′。因此,如果目标空间较大,x b _{b} b? 离粒子群的初始位置较远(在处理 CMOP 时通常会出现这种情况),收敛到 x b _{b} b? 的速度就会很慢,因为 x l _{l} l? 无法超过 x w _{w} w? 以接近 CPS。

- 图1. iCSO的搜索行为分析。(a)当种群距离Pareto最优解 x b x_b xb?较远时,收敛到 x b x_b xb?的速度较慢。(b)当解的质量相同时,向胜者学习不能帮助跳出局部最优。
图1(b)描述了另一种情况,iCSO 将粒子分为 winners and losers,然后将 losers 推向 winners。如果粒子群陷入局部最优(即,相同的局部最优非支配前沿),iCSO 无法区分 winners 和 losers ,因为所有的粒子都是相同的 fitness 值。在这种情况下,速度v和矢量 Δ ′ \Delta^{\prime} Δ′具有相同的方向。这样,向 winner 学习对于 loser 跳出局部最优或局部可行域是无效的。如图 1 (b)所示, x w x_w xw?和 x l x_l xl? 越来越接近,但无法收敛到 x b x_b xb?。
为了验证上述情况,我们选择了两个具有代表性的 CMOPs,DC2-DTLZ1 和 LIR-CMOP8。DC2-DTLZ1包含内外两层(内外层)可行域,使其收敛困难且可行困难,而 LIR-CMOP8 存在较大的不可行域。图 2 为采用文献[12]默认参数设置的iCSO结果,IGD 值在 30 次运行中位数。
1)如图 2 (a)-(c)所示,粒子群收敛非常缓慢。从第300代到第500代,粒子很少运动。这是由于DC2-DTLZ1是收敛困难的,iCSO的种群与真实的CPF相差较远,导致iCSO的更新策略收敛较慢。
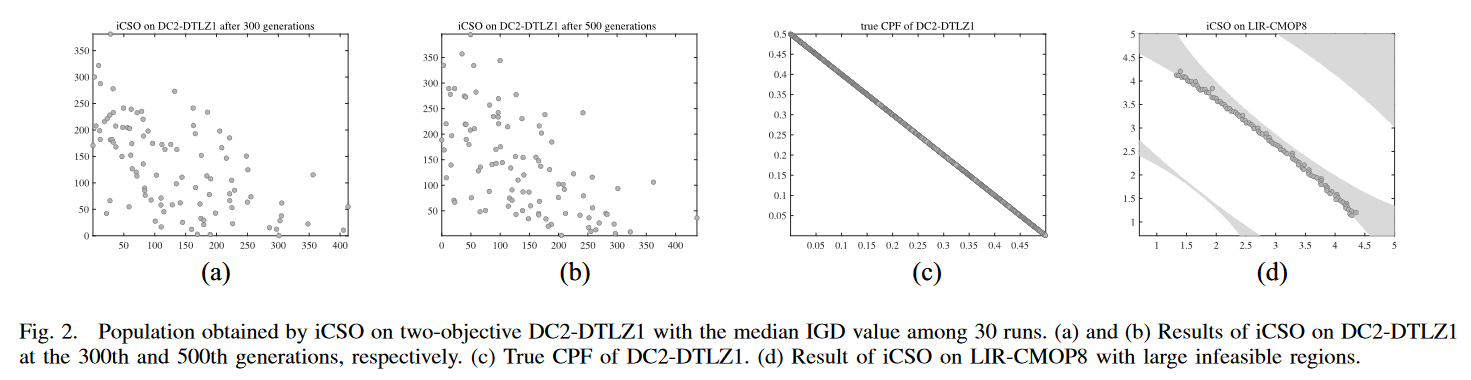
- 图2. iCSO在两目标DC2-DTLZ1上得到的种群在30次运行中IGD值的中位数。(a)和(b)分别为第300代和第500代DC2-DTLZ1的iCSO结果。(c) DC2-DTLZ1 的真CPF. (d) 不可行区域较大的LIR-CMOP8的iCSO结果。
2)如图2(d)所示,在LIR-CMOP8上,种群被捕获到具有相同非支配前沿的外层可行域中。这样,swarm 就很难移动到真正的内层CPF。
为了弥补iCSO的这些缺陷,本文在第三节提出了一个CCSO和一个新的CMOEA ( CMOCSO )。
III. OUR APPROACH
A. CCSO
CCSO算法在iCSO算法的基础上增加了一个iCSO算法,并针对iCSO算法的不足提出了一种新的协同群优化算法。
1)提出的竞争群优化算法(Proposed Competitive Swarm Optimizer): 提出的CSO采用了一种新的更新策略,具有更快的收敛速度
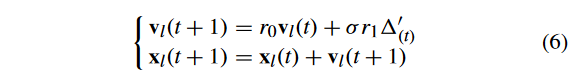
式中:σ为扩展因子,由:

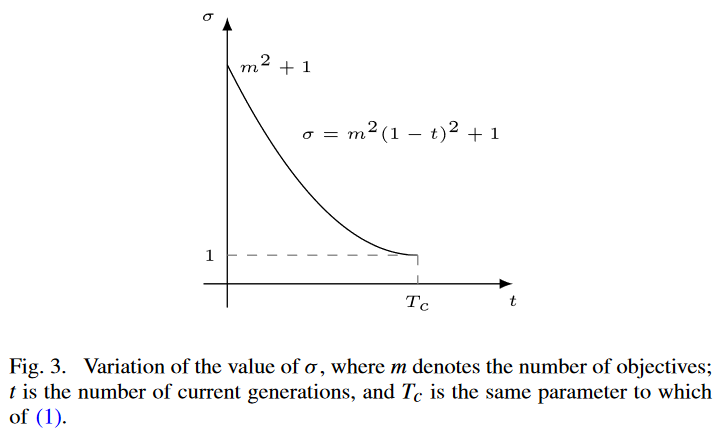
式中:m 为目标函数个数;t 为当前一代的迭代次数;和 T c T_c Tc? 为最大代数,与式(1)相同。 σ σ σ 的变化如图3所示。根据这一变化规律,随着世代数 t t t 的增加, σ σ σ 从 m 2 + 1 m^2 + 1 m2+1 减小到 1。此外,随着 t t t 的增加,梯度逐渐减小。因此, σ σ σ 值在演化的早期阶段急剧下降,而在演化的后期阶段只有轻微的下降。这样,在早期阶段扩展较大,以加速收敛到 CPF,但在后期阶段扩展较小,以确保 CPF 的开发能力。
2)提出了协同群优化算法(Proposed Cooperative Swarm Optimizer): 对于协同群优化算法,基于算术交叉算子,粒子 x w x_w xw? 和 x l x_l xl? 的更新策略如下:
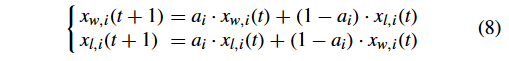
其中, a i a_i ai? 为每个变量随机生成 0 或 1, i = 1 , . . , n i = 1,..,n i=1,..,n 在这种情况下, x w x_w xw?和 x l x_l xl?的决策变量是随机交换的,而不是从一个学习到另一个。
众所周知,进化计算社区中 “cooperative” 的一般含义是种群或群体之间的合作,即协同进化。然而,我们提出的方法中的协同是在粒子层面上两两粒子之间协同学习的思想。传统的 PSO 或 CSO 通过向一个更好的粒子学习来更新一个更坏的粒子的位置。在我们提出的协同群优化算法中,一种新颖的更新方法是通过允许一个粒子的适应度变差,即牺牲一个粒子来使另一个粒子变好来实现的。换句话说,它是对 PSO/CSO 的一种改进。
相比于 iCSO 将粒子划分为 winners-losers,并将每个 loser 转移到 winner,协同群优化器允许一个粒子的适应度变差以使另一个更好,旨在克服 iCSO 在处理 CMOPs 时的不足,如图 2(d)所示。
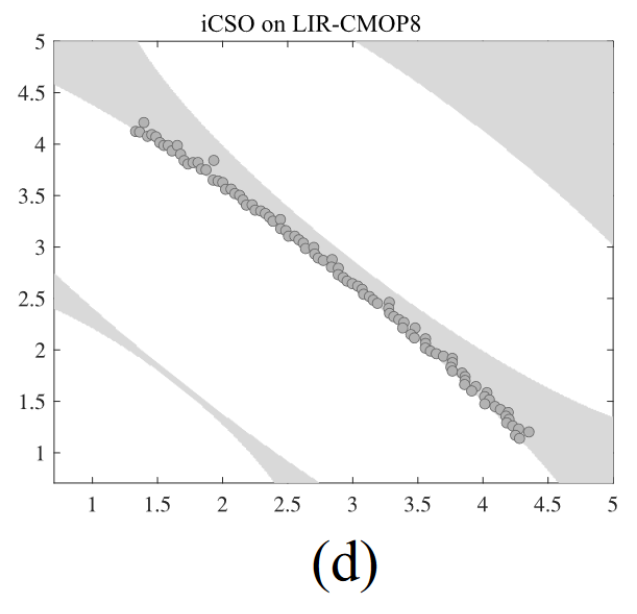
3)分析: 为了分析CCSO的搜索行为,两个 artificial scenarios 如图 4 所示。
- 1) 图 4 (a) 描绘了 loser solution x l x_l xl?向 winner solution x w x_w xw?学习的搜索轨迹。根据扩展因子σ, x l x_l xl?可以超过 x w x_w xw?,因为 σ r 1 Δ ′ \sigma r_1\Delta^{\prime} σr1?Δ′ 大于 r 1 Δ ′ r_1\Delta^{\prime} r1?Δ′。此外,随着σ的减小,延伸量也随之减小。因此,如果 x w x_w xw? 在后期近似 x b x_b xb?,则 x l x_l xl? 可以在 x w x_w xw? 附近搜索,以确保CPF的开发。
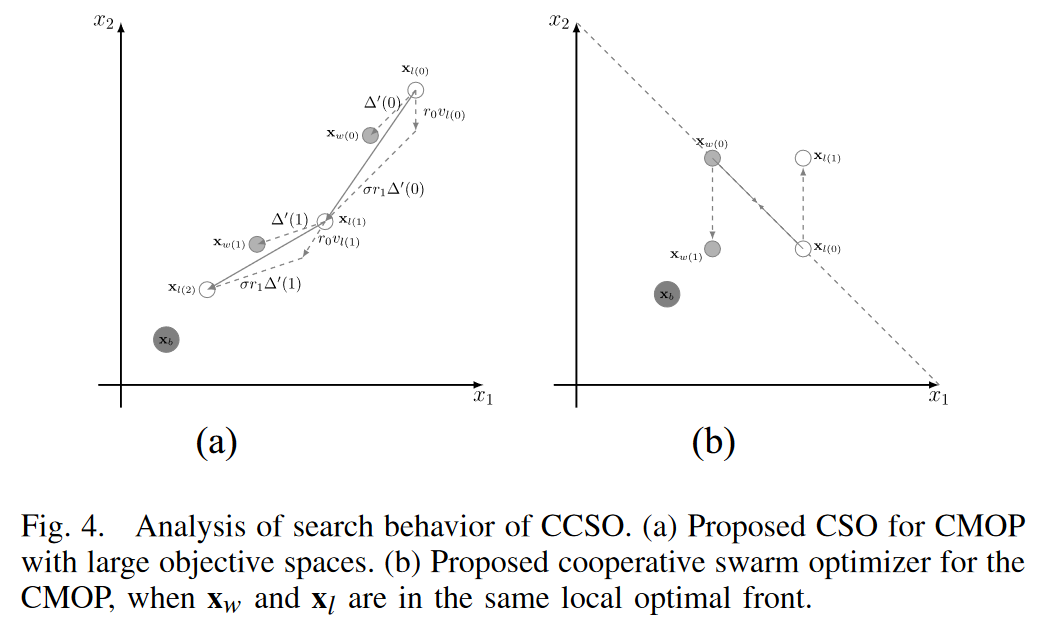
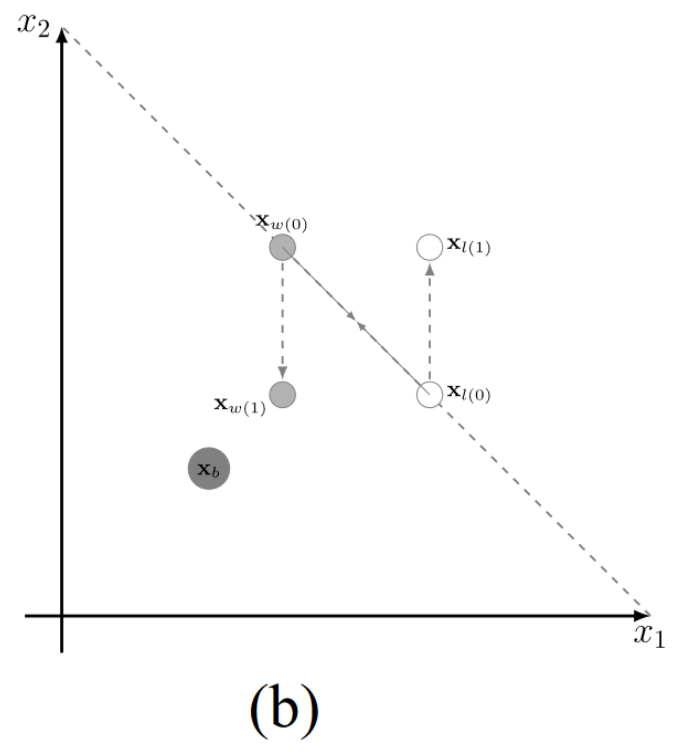
2) 图 4 (b) 展示了两个解 x w x_w xw?和 x l x_l xl? 位于同一个非支配前沿的情形。With the cooperative swarm optimizer,产生了两个新的解[即 x w ( 1 ) x_{w(1)} xw(1)? 和 x l ( 1 ) x_{l(1)} xl(1)?] .因此,新产生的 winner solution x w ( 1 ) x_{w(1)} xw(1)? 能够跳出局部最优,更接近于 x b x_b xb?。
为了更好地了解CCSO的有效性,对四种CMOPs进行了初步实验:1) C1-DTLZ3 (多模态);2 ) DAS-CMOP5 (收敛);3 ) DC3-DTLZ1 (内-外可行层);4) LIR-CMOP5 (大的不可行域) .其中,C1-DTLZ3和DC3 - DTLZ1是三目标CMOPs,另外两个实例是双目标CMOPs。将CCSO和iCSO在30次运行中IGD值居中的所选算例上的收敛结果绘制在图5中。可以观察到CCSO在这四个实例上的收敛速度比iCSO快,而iCSO在这四个实例上的收敛速度较慢,不能保证对CPF的逼近。然而,CCSO能够收敛到CPF,并在0附近逼近IGD值。
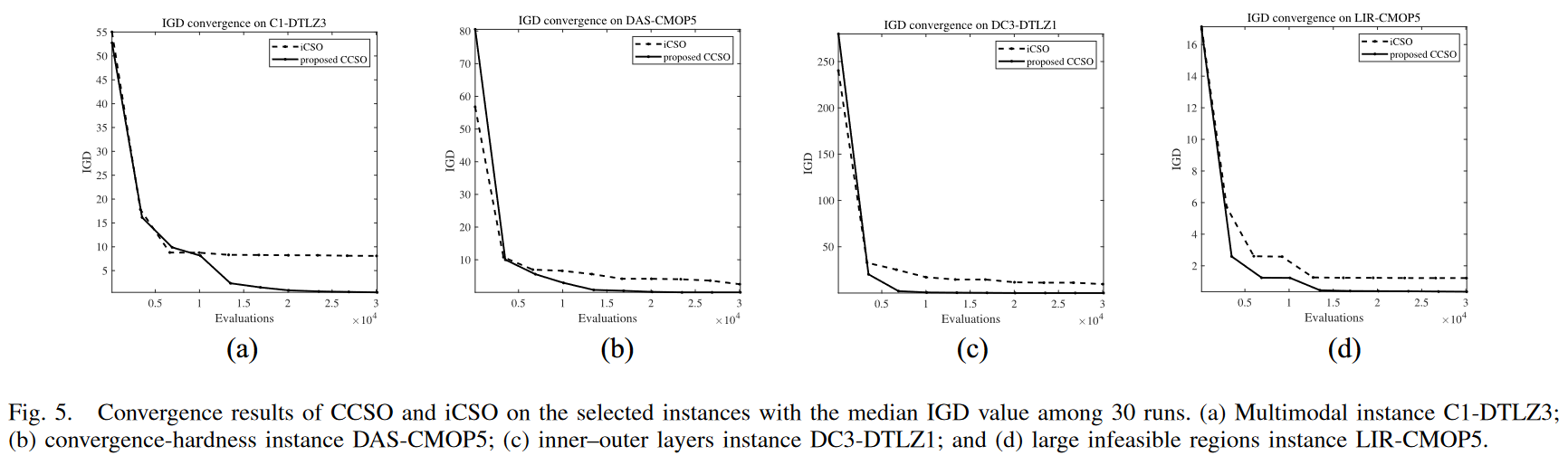
- 图 5.CCSO 和 iCSO 在 IGD 值中位数为 30 次的算例上的收敛结果。(a)多模态实例C1-DTLZ3;(b)收敛-硬度实例DAS-CMOP5;(c)内外两层实例DC3-DTLZ1;(d)大的不可行区域实例LIR-CMOP5。
当CMOP具有较大的目标空间(如C1-DTLZ3和DC3-DTLZ1 )或收敛困难(如DAS-CMOP5 )时,iCSO不能收敛到CPF,导致较大的IGD值。然而,由于CCSO中的CSO通过扩展因子提供了更快的逼近CPF的速度,因此所提出的CCSO可以收敛到CPF。在处理C1-DTLZ3等多模态景观、DC3-DTLZ1等可行域内-外层或LIR-CMOP5等较大不可行域的CMOPs时,当胜者和失败者粒子性能相同时,iCSO 不能跳出局部最优,因为向其他粒子学习不能帮助逃离局部最优,从而导致较大的IGD值。然而,CCSO 可以找到CPF ,因为协作群优化器可以通过协作学习模型产生局部最优区域外的粒子,如图 4(b) 所示。
B. Framework of CMOCSO
在CCSO的基础上,提出了一个新的CMOEA,即 CMOCSO,用于解决CMOPs。CMOCSO 框架如算法1所示。首先,随机生成两个初始种群 P 1 \mathcal{P}_{1} P1?和 P 2 \mathcal{P}_{2} P2? (第 1 行)。主群 P \mathcal{P} P 作为最终的输出,由算法 2 (行2 )中的 “Selection()” 得到。然后,继续进行下面的步骤,直到满足终止条件(即 t > T t > T t>T),其中 t 是当前代计数器,T 是最大代数。


为了更好地探索可行区域,本文采用 ε 约束松弛技术作为 P 1 \mathcal{P}_{1} P1? (line 5) 的 CHT,因为它可以保留一些有前途的不可行解来探索未检测到的可行区域 [19]。正如文献[35]所提出的,ε 更新如下:
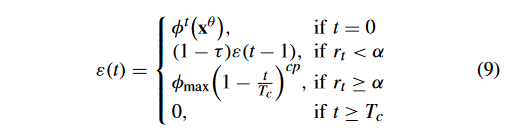
其中, ? t ( x θ ) \phi^t(\mathbf{x}^\theta) ?t(xθ) 是初始种群 P 1 \mathcal{P}_1 P1?中前 θ % \theta \% θ% 个体的总 CV , r t r_t rt? 是 P 1 \mathcal{P}_1 P1? 可行比率; τ \tau τ 和 α \alpha α 是两个控制参数; ? m a x \phi_\mathrm{max} ?max?是目前发现的 P 1 \mathcal{P}_{1} P1?的最大CV值; T c T_c Tc?控制 ε \varepsilon ε工作的最大迭代,而 c p cp cp用于控制在 r k ≥ α r_k\geq\alpha rk?≥α情况下降低 ε \varepsilon ε值的速度。
虽然(9)遵循与(2)相同的规则,但工作原理不同。在PPS [35]中,存在一个推阶段,该阶段忽略约束,将种群推向无约束PF,其中(2)是在该阶段中提出的。在推送阶段,不使用 ε。但是在CMOCSO中,由于没有这样的阶段,当 t < T c t < T_c t<Tc? 时,ε 在整个搜索过程中都在更新,也就是说约束松弛的作用时间更长。
然后,根据 ““CompetitiveUpdate()” 生成 P 1 \mathcal{P}_1 P1? (即 P 1 ′ \mathcal{P}_1^{'} P1′? )的子代种群,如算法 1 (第6行)所示。然后,将 P 1 \mathcal{P}_1 P1? 和 P 1 ′ \mathcal{P}_1^{'} P1′? 合并,执行 “Selection()” 过程,形成新的 P 1 \mathcal{P}_1 P1? (第7行)。(CompetitiveUpdate() 见算法 3)

类似地, P 2 \mathcal{P}_2 P2? 的子代群体 P 2 ′ \mathcal{P}_2^{'} P2′? 是基于 “CooperativeUpdate()” 产生的,如算法 1 (第 8 行)所示。然后,将 P 2 \mathcal{P}_2 P2? 和 P 2 ′ \mathcal{P}_2^{'} P2′? 合并,执行’ Selection( ) '过程,形成新的 P 2 \mathcal{P}_2 P2? ( line 9 )。最后,更新 main swarm P \mathcal{P} P,如第10行所示。(CooperativeUpdate() 见算法 4)

1)选择: 算法 2 给出了"Selection() "过程。首先,将选择的 swarm P ′ \mathcal{P}^{'} P′ 初始化为空。那么, P \mathcal{P} P 中粒子的适应值根据如下计算:
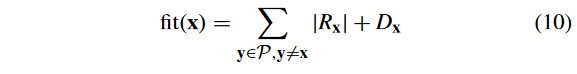
式中: R x R_x Rx? 表示可行性和收敛性评价,计算式为
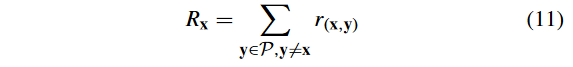
其中, r ( x , y ) r( x , y) r(x,y) 定义为
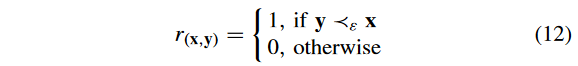
其中, y ? ε x y?_ε x y?ε?x 表示 y ? ε y~ ε y?ε-支配 x x x 。注意到,如果 ε = 0 ε = 0 ε=0,则 ? ε ?ε ?ε 作为CDP起作用;若 ε = ∞ ε =∞ ε=∞,则 ? ε ?ε ?ε 为传统的帕累托占优。
D x D_x Dx? 表示多样性的评价,计算为:
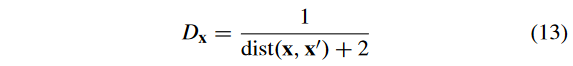
式中: d i s t ( x , x ′ ) dist( x , x^′) dist(x,x′) 为目标空间中 x x x 到 P \mathcal{P} P 的最近邻点的欧氏距离。这种适应度评价策略起源于 SPEA2 [36],已被证明在实现收敛性和多样性之间的平衡方面非常有效[37] [38]。
然后,采用SPEA2 [36]的选择过程对下一代(第3~9行)的粒子群进行选择。最后, P ′ \mathcal{P}^{'} P′ 为输出( 12行)。

2)备注: 值得注意的是,对于第7行、第9行和第10行的" Selection() "过程,不同的 different swarms 使用不同的 ε 值。
- 1)在第7行中,利用约束松弛因子 ε 可以保留部分不可行解,以更好地探索未被发现的不可行区域[19]。因此,对 P 1 ′ \mathcal{P}_1^{'} P1′? 采用ε-约束技术,加强对可行域的探索。
- 2)在第9行,如CCMO [15]所分析的,忽略约束(即 ε = ∞ ε =∞ ε=∞)可以通过将解推向PF来帮助CPF的逼近。因此,对 P 2 \mathcal{P}_2 P2?采用 ε = ∞ ε =∞ ε=∞,以增强合作种群跳出局部最优的能力。
- 3)在第10行中,通过设置ε = 0,对 P \mathcal{P} P使用CDP,原因是CDP对可行解具有偏好性,可以保证 P \mathcal{P} P仅由可行解组成作为最终输出。
因此, P 1 \mathcal{P}_1 P1? (约束松弛)、 P 2 \mathcal{P}_2 P2? (约束忽略)和 P \mathcal{P} P (约束优先)的配合为CMOCSO更好地处理约束提供了更加多样化的约束优先级。
C. Generation of Offspring Swarms Based on CCSO
基于CCSO的子代 swarms 的产生分别是 “CompetitiveUpdate()” 和 “CooperativeUpdate()”。这两个过程在算法3和算法4中给出。
1)竞争更新过程:算法 3 中的 “CompetitiveUpdate()” 过程如下:
- 1)根据式(10)评估 P \mathcal{P} P中粒子的适应度值,其中 ε(g)作为约束松弛因子(第1行)。
- 2)然后,初始化子代 swarm P 1 ′ \mathcal{P}_1^{'} P1′?为空(第2行)。
- 3)直到 P \mathcal{P} P的大小为空,继续进行下面的步骤。首先,从 P \mathcal{P} P (第4行)中随机选取两个粒子p和q。从 P \mathcal{P} P (第5行)中去掉。之后,根据适应度值(第6 ~ 12行)来检测 winner and loser。然后,loser 基于(6) (第13行)向 winner 学习。此外,在 iCSO [12] 中使用多项式变异(PM) [13] 来提高跳出局部最优的性能。 最后,将生成的 x w ′ x^′_w xw′?和 x l ′ x^′_l xl′?添加到 P 1 ′ \mathcal{P}_1^{'} P1′? (第15行)中。
2)协同更新过程:算法 4 所示的 "CooperativeUpdate() " 过程如下。
- 1)根据式 (10) 评估 P \mathcal{P} P中粒子的适应度值,其中 ε = 0 用来忽略约束条件来近似PF和CPF (第1行)。
- 2)分析可知,设计协同优化器是为了跳出局部最优。因此,处于局部最优的粒子应该被赋予更高的执行协同优化器的可能性。因此,首先选择一个学习池,该池中的粒子执行协同优化器(第2行)。学习池的选择在算法 5 中给出。
- 3 )然后,初始化子代粒子群 P ′ \mathcal{P}^{'} P′为空(第2行)。
- 4 )直到 P ′ \mathcal{P}^{'} P′的大小满足N,进行下面的步骤。首先,从P (第5行)中随机选取两个粒子 x w x_w xw?和 x l x_l xl?。然后,它们通过( 8 ) (第6行)相互学习来更新。执行PM [ 13 ]以提高子代逃离局部最优的能力(第7行)。最后,将生成的 x w ′ x^′_w xw′?和 x l ′ x^′_l xl′?添加到 P ′ \mathcal{P}^{'} P′( line 8 )中。
**3)学习池的选择:学习池的选择在算法 5 中给出。**在 "LearningPoolSelection() " 过程中使用了锦标赛选择。具体来说,执行如下步骤:首先,将学习池 L \mathcal{L} L 初始化为空(第1行)。直到 L \mathcal{L} L 的大小满足 N,以下步骤重复(第2 ~ 11行)。
- 1 )从 P \mathcal{P} P中随机选择x和y;
- 2 )如果x优于y,则在 L \mathcal{L} L中添加x;
- 3 )如果y优于x,则在 L \mathcal{L} L中添加y;
- 4 )如果x等于y,则在 L \mathcal{L} L中随机选择两个粒子中的一个粒子添加。

D. Computational Complexity
CMOCSO 主要包括"Selection()"、"CompetitiveUpdate() "、“CooperativeUpdate()” 和 “LearningPoolSelection()” . 它们的计算复杂度分别为 O ( N 3 ) , O ( m N 2 ) , O ( m N 2 ) O ( N^3 ),O ( mN^2 ),O ( mN^2 ) O(N3),O(mN2),O(mN2)和 O ( N ) O ( N ) O(N)。因此,CMOCSO的整体计算复杂度为 O ( N 3 ) O ( N^3 ) O(N3)。
IV. RESULTS AND ANALYSIS
本部分通过实验研究考察了CMOCSO在求解CMOPs / LSCMOPs时的性能。所有的实验都是在PlatEMO [ 39 ]上进行的。
A. Experimental Settings
1)算法比较:将CMOCSO算法与其他先进算法进行比较。
- 1)对于 small-scale CMOPs,我们选取了 C-TAEA [40],CMOEAMS [37], NSGA-II-ToR [14], PPS [35],ToP[41], and LMOCSO [12] . 在这些 CMOEAs中,ToP 和 PPS 使用 DE 作为遗传算子;C-TAEA, CMOEA-MS, and NSGA-II-ToR 采用 GA 作为遗传算子;和 LMOCSO 采用 iCSO 作为遗传算子。
- 2)对于 LSCMOPs,选择 POCEA [42], IMMOEA [43], DGEA [44], CMOPSO [10], and LMOCSO [12]。其中,CMOPSO 和 LMOCSO 使用 CSO 作为遗传算子,而其他方法使用不同的遗传算子。
2)基准问题:为了广泛验证CMOCSO的有效性,实验研究中使用了4个广泛使用的基准 CMOP:1) DTLZ (C-DTLZ [45] and DC-DTLZ [40]);2) MW [46];3) LIR-CMOP [19]; and 4) DAS-CMOP [47].。根据这些基准的特征,它们被分为三类。
- 1)第1组( DTLZ ):DTLZ基准包括10个C-DTLZ和DC-DTLZ实例,有3个目标。C-DTLZ问题相对简单;它们的困难主要是由大的目标空间和各种CPF形状(规则和不规则)造成的。对于DC-DTLZ问题,其难点在于不连续的CPF形状和内外层可行域,使得算法容易陷入局部最优。
- 2)第2组(DAS-CMOP和LIR-CMOP):DASCMOP基准测试集包含9个实例,具有可行性-硬度、收敛性-硬度和多样性-硬度特征。它们对现有的CMOEAs提出了挑战,因为算法需要平衡可行性、收敛性和多样性,以在DAS-CMOPs上取得良好的性能。LIR-CMOP套件共有14个实例。它们的困难主要是由较大的不可行域造成的,这些不可行域使得算法容易陷入局部可行域。
- 3)第3组(MW):在MW套件中,共有14个算例,包括4种不同的PF和CPF的几何关系。由于不存在复杂的约束或不可行区域,除了MW4、MW8和MW14这3个目标外,是一个相对简单的测试集。
小规模情形的决策变量个数n和目标函数个数m如下。
-
- DTLZ:对于C1-DTLZ1,DC1-DTLZ1,DC2-DTLZ1和DC3-DTLZ1,n = 7;对于其他实例,n = 12;M = 3 .
-
- MW:MW4、MW8和MW14的n = 15和m = 3;其他情况M = 2。
-
- LIR-CMOP:LIR-CMOP13和LIR-CMOP14的n = 30,m = 3;其他情况M = 2。
-
- DAS-CMOP:DAS-CMOP7~DAS-CMOP9,n = 30,m = 3;其他情况M = 2。
对于大规模问题,在DTLZ和LIR-CMOP测试用例上分别使用n = 50,100,150。
3)遗传算子和参数设置:PPS and ToP 采用DE算子,而其他对比算法均采用GA算子。对于使用GA算子的算法,使用模拟二进制交叉(SBX) [48]和PM [13],并进行以下参数设置。
- 1)交叉概率 p c = 1 p_c = 1 pc?=1;分布指数为 η c = 20 η_c = 20 ηc?=20。
- 2)变异概率 p m = 1 / n p_m = 1 / n pm?=1/n;分布指数为 η m = 20 η_m = 20 ηm?=20。
对于使用DE算子的CMOEAs,DE中CR和F的参数分别设置为1和0.5。
所有方法的种群规模N均为91。对于DTLZ和MW,函数估计的最大次数 E m a x E_{max} Emax?设置为 80000;120 000 for LIR-CMOP and DAS-CMOP. 。对于50-D、100-D 和 150-D DTLZ, E m a x E_{max} Emax?分别设置为 800 000、2 000 000和3 000 000。为了公平比较,所有算法都使用这些设置。( 9 )中的参数设置与[ 35 ]相同。在处理现实世界中不同的CMOP时,这些参数可以根据[ 35 ]的实验进行调整。用于比较的其他算法的参数设置与他们的原始论文中建议的相同。除非提及改变,所有参数设置保持不变。
4)性能指标:为了评估不同算法的性能,采用基于改进距离计算的反向世代距离(IGD +) [ 49 ]和超体积(HV) [ 50 ]作为性能指标。采用IGD +是因为IGD [ 51 ]是帕累托无抱怨的,这两个指标在性能比较中可以提供更强的可靠性[ 52 ]。
-
- IGD +:IGD +表示真实PF上的每个参考点到最近个体的平均距离。设 S ? S^* S? 为PF上均匀分布的点集, S S S为解集。然后,计算 I G D + IGD+ IGD+ 值
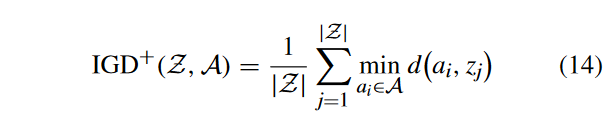
式中:a和z之间的距离
d
(
a
i
,
z
j
)
d( a_i , z_j)
d(ai?,zj?)计算如下:
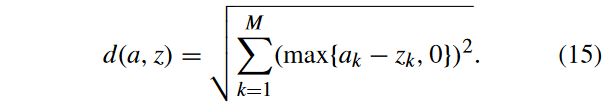
IGD +值越小,性能越好。
-
- HV:HV衡量了所求解集与预定义参考点 z r z^r zr所围成的目标空间的HV。解集S的HV值可表示为如下形式:
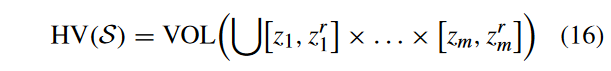
其中,VOL表示Lebesgue测度。HV值越大,性能越好。
根据文献[53]的方法,在真实PF上采样10000个均匀分布的点,用于IGD +的计算。首先对目标值进行归一化处理,然后在归一化后的目标空间中,采用( 1.1 , 1.1 , … , 1.1)作为HV计算的参考点。
每个算法在每个测试实例上执行30次以上的独立运行。记录IGD +和HV的平均值和标准差。采用显著性水平为0.05的Bonferroni校正的Friedman检验和显著性水平为0.05的Wilcoxon秩和检验,借助KEEL软件进行统计分析[ 54 ]。此外,使用’ +,’ ’ -,‘和’ = ‘来表明,根据Wilcoxon检验,该算法的结果显著优于,显著差于或统计上与CMOCSO获得的结果相似。’ NaN '值表明算法无法找到可行解。
B. Influence of Different Components in CMOSCO
为了研究CMOSCO中不同元件的有效性和必要性,设计了以下5种CMOSCO变体。
-
- CMOCSO1:仅使用提出的CSO。
-
- CMOCSO2:仅使用提出的协同群优化算法。
-
- CMOCSO3:用CDP代替ε-constraint技术。
-
- CMOCSO4:将提出的CSO替换为iCSO。
-
- CMOCSO5:将提出的CSO的swarm P 1 \mathcal{P}_1 P1?作为最终输出。
这五个变体以及CMOCSO在四个基准测试集(即DTLZ、MW、LIR - CMOP和DASCMOP)上进行了测试。
1)关于第1组基准:在补充材料中,表S-I和S-II分别显示了第1组CMOPs的HV和IGD+结果。显然,CMOCSO优于除CMOCSO2外的其他变体。CMOCSO2的结果优于CMOCSO。这是因为DTLZ问题的可行域有内层和外层,且这些问题的CPF接近PF,CMOCSO2只使用协同群优化算法,更适合DTLZ问题。
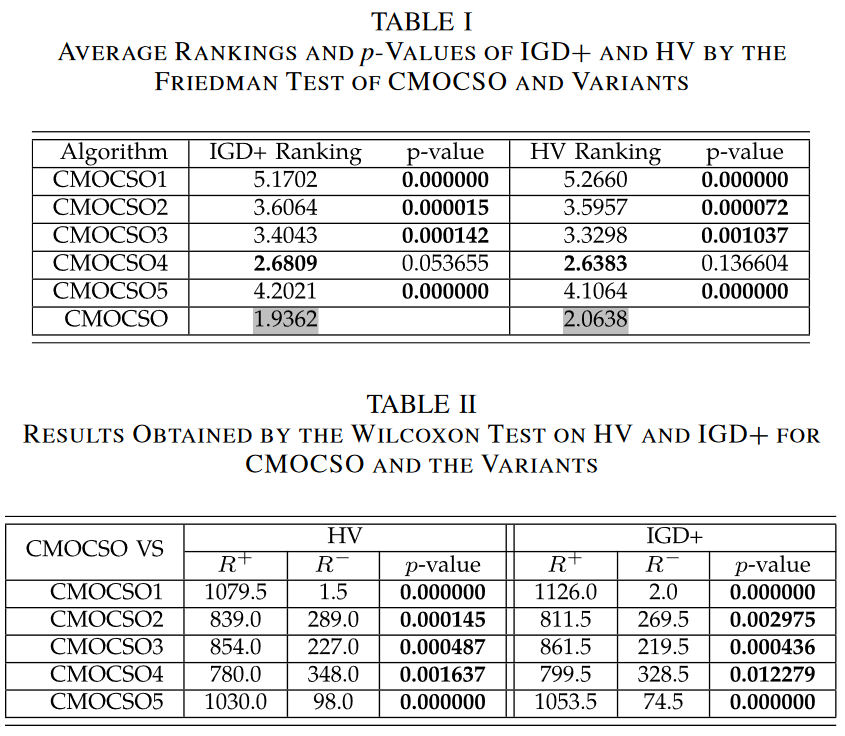
2)第2组基准:在补充材料中,表S-III和S-IV分别报告了第2组CMOPs的HV和IGD +结果。可以看出,在23个算例中的17个算例上,CMOCSO对于复杂约束区域的问题取得了最好的结果。然而,在其他6个例子上,CMOCSO比一些变体更差:1) DAS-CMOP4和DAS-CMOP5具有可行性-困难性;因此,由于CPD比ε-约束技术更关注可行解,因此采用CDP的CMOCSO3表现更好;2)在LIR-CMOP11和LIR-CMOP12上,CMOCSO比CMOCSO4更差,因为它们的CPFs离PFs较远,可行域较小。因此,收敛速度较慢的iCSO在这些问题上具有更好的搜索能力;3) LIR-CMOP13和LIR-CMOP14问题类似于DTLZ问题。CMOCSO2表现优于CMOCSO。
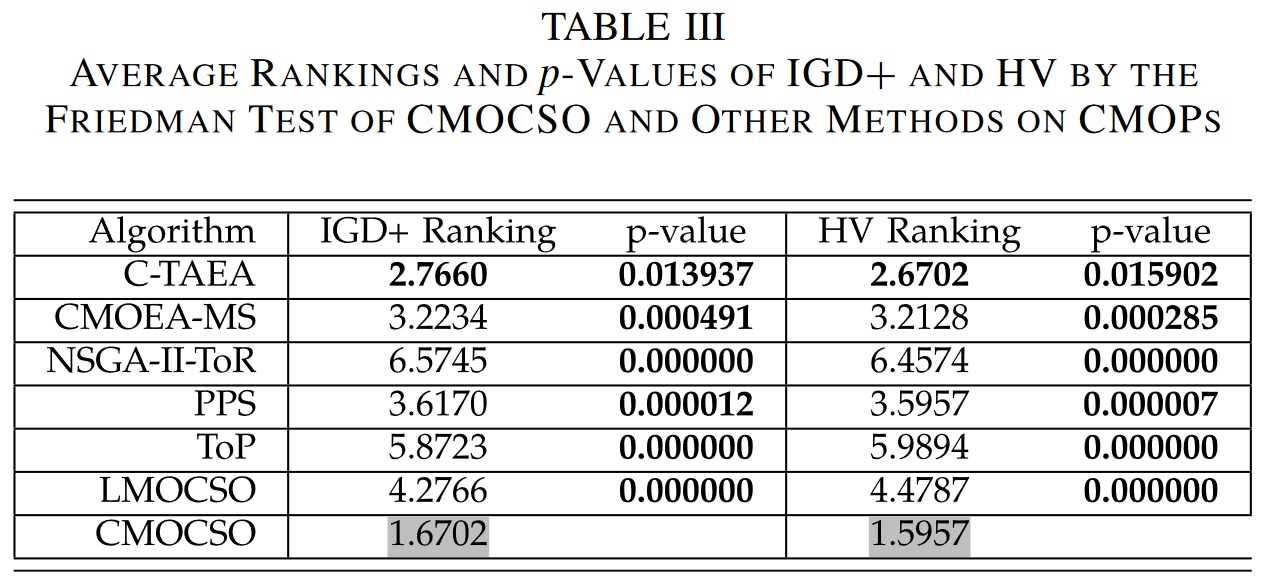
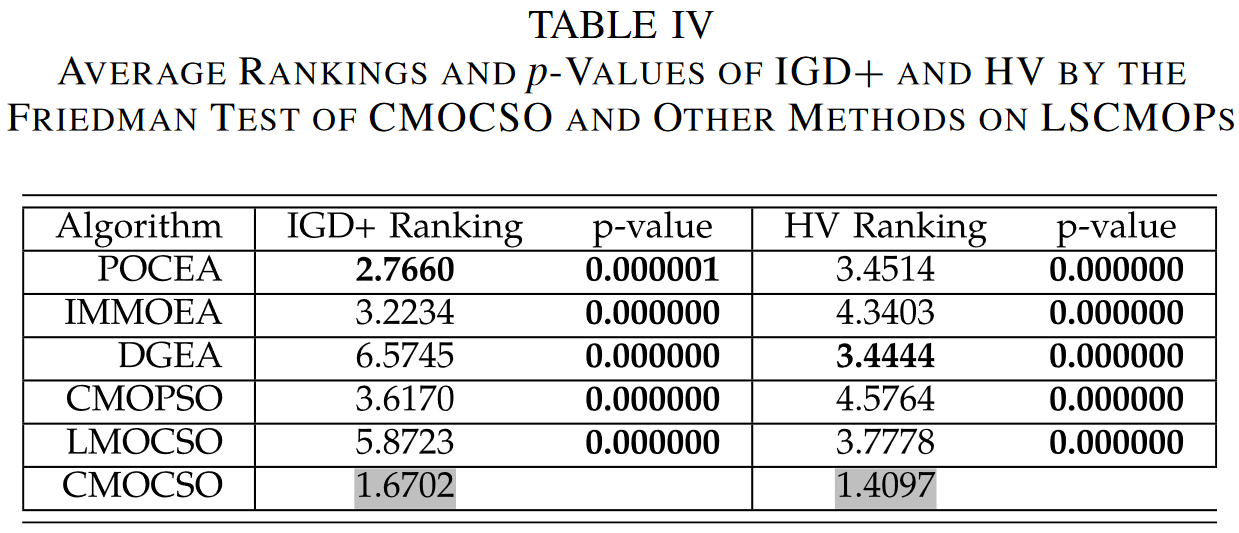
3)第3组基准:在补充材料中,表S-V和S-VI分别显示了第3组CMOPs的HV和IGD +结果。由于MW算例相对简单,CMOCSO2、CMOCSO3和CMOCSO4比CMOCSO具有更好或更有竞争力的结果。其原因是CPF在MW上靠近PF。对于这些相对简单的问题,忽略约束(即CMOCSO2)或使用CDP (即CMOCSO3)或仅仅使用iCSO (即: CMOCSO4)都可以获得很好的结果。
V. CONCLUSION
在本文中,提出了一种CCSO来加速收敛,增强跳出局部最优和局部可行域的能力。在CCSO的基础上,针对CMOPs提出了CMOCSO。大量的实验结果证明了CMOCSO方法相对于其他方法的优越性。此外,CMOCSO对LSCMOPs以及现实问题的有效性也得到了验证。
并对未来的一些方向进行了展望:
- 1)从结果中我们发现CMOCSO不能很好地消除极值点,导致在一些算例上表现不佳,特别是在一些DTLZ算例上,未来将在CMOCSO中集成消除极值点的技术。
-
- CMOCSO对LIR-CMOP7-9和LIR-CMOP12的无效性表明,当不可行域较大且复杂时,当前的CMOCSO不能找到CPF的所有部分。设计更好的ε更新策略可能是一种可能的解决方案。
- 3)实验结果验证了CMOCSO对LSCMOPs的有效性,表明其具有良好的发展前景。然而,考虑到时间复杂度为 O ( N 3 ) O(N^3) O(N3),一些耗时较少的CCSO技术被寄予厚望。
- 4)从第IV-D节中,我们发现CMOCSO在LSCMOPs上表现良好。更深入地分析原因并将CMOCSO扩展到具有更高决策维度的LSCMOPs将是有价值和前景的。
References
F. Ming, W. Gong, D. Li, L. Wang and L. Gao, “A Competitive and Cooperative Swarm Optimizer for Constrained Multiobjective Optimization Problems,” in IEEE Transactions on Evolutionary Computation, vol. 27, no. 5, pp. 1313-1326, Oct. 2023, doi: 10.1109/TEVC.2022.3199775.
文章核心分析
iCSO 的缺陷
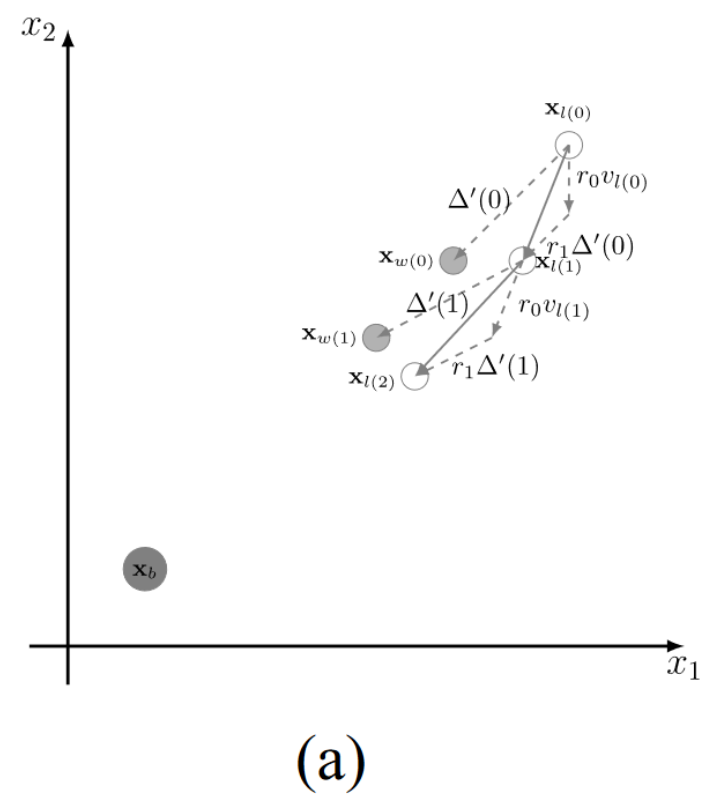

如图 (a) 所示,通过向 x w ( 0 ) \mathbf{x}_{w}(0) xw?(0) 学习, x l ( 0 ) x_l(0) xl?(0) 移动到 x l ( 1 ) _l(1) l?(1);然后,通过向 x w ( 1 ) \mathbf{x}_{w}(1) xw?(1) 学习, x l ( 1 ) x_l(1) xl?(1) 移动到 x l ( 2 ) x_l(2) xl?(2)。这样,粒子可以通过向更好的粒子(即winner particle)学习,逐渐逼近 x b x_b xb?,然而,如图所示, r 1 Δ ′ r_1\Delta^{\prime} r1?Δ′ 总是小于 Δ ′ \Delta^{\prime} Δ′。因此,如果目标空间较大,x b _{b} b? 离粒子群的初始位置较远(在处理 CMOP 时通常会出现这种情况),收敛到 x b _{b} b? 的速度就会很慢,因为 x l _{l} l? 无法超过 x w _{w} w? 以接近 CPS。
Δ ′ \Delta^{\prime} Δ′ = x w ? x l \mathbf{x}_{w} - \mathbf{x}_l xw??xl? 的一个向量,其中 x w 、 x l \mathbf{x}_{w} 、 \mathbf{x}_l xw?、xl? 为迭代次数为 t 时的位置
图1(b)描述了另一种情况,iCSO 将粒子分为 winners and losers,然后将 losers 推向 winners。如果粒子群陷入局部最优(即,相同的局部最优非支配前沿),iCSO 无法区分 winners 和 losers ,因为所有的粒子都是相同的 fitness 值。在这种情况下,速度v和矢量 Δ ′ \Delta^{\prime} Δ′具有相同的方向。这样,向 winner 学习对于 loser 跳出局部最优或局部可行域是无效的。如图 1 (b)所示, x w x_w xw?和 x l x_l xl? 越来越接近,但无法收敛到 x b x_b xb?。
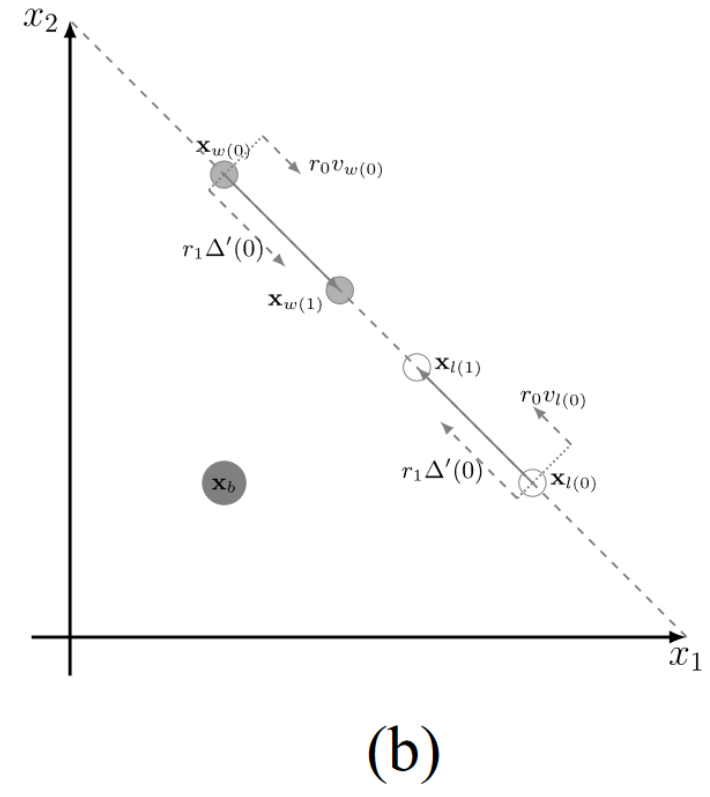
为了验证上述情况,我们选择了两个具有代表性的 CMOPs,DC2-DTLZ1 和 LIR-CMOP8。DC2-DTLZ1包含内外两层(内外层)可行域,使其收敛困难且可行困难,而 LIR-CMOP8 存在较大的不可行域。图 2 为采用文献[12]默认参数设置的iCSO结果,IGD 值在 30 次运行中位数。
1)如图 (a)-(c)所示,粒子群收敛非常缓慢。从第300代到第500代,粒子很少运动。这是由于DC2-DTLZ1是收敛困难的,iCSO的种群与真实的CPF相差较远,导致iCSO的更新策略收敛较慢。
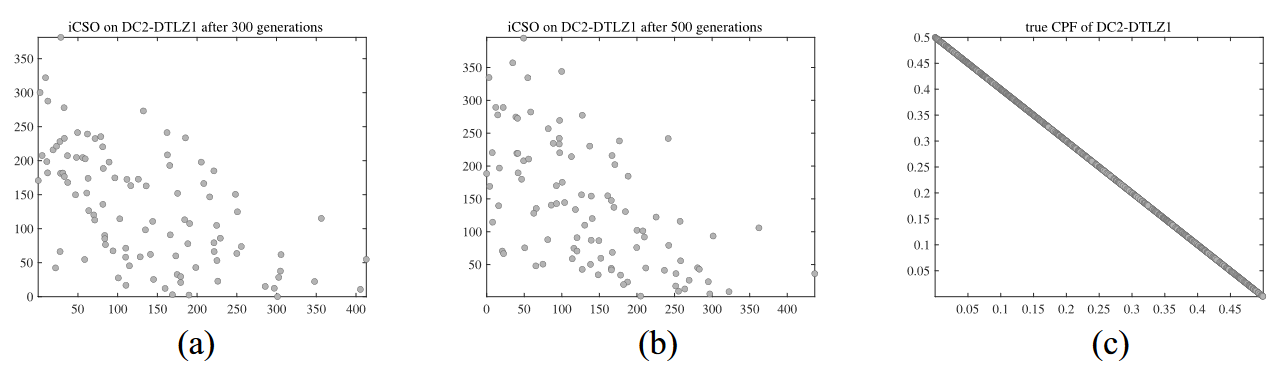
2)如图2(d)所示,在LIR-CMOP8上,种群被捕获到具有相同非支配前沿的外层可行域中。这样,swarm 就很难移动到真正的内层CPF。
本文的解决方案见第三章
CCSO
1)提出的竞争群优化算法(Proposed Competitive Swarm Optimizer): 提出的CSO采用了一种新的更新策略,具有更快的收敛速度
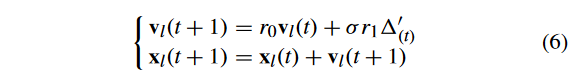
式中:σ为扩展因子,由:

式中:m 为目标函数个数;t 为当前一代的迭代次数;和 T c T_c Tc? 为最大代数,与式(1)相同。 σ σ σ 的变化如图3所示。根据这一变化规律,随着世代数 t t t 的增加, σ σ σ 从 m 2 + 1 m^2 + 1 m2+1 减小到 1。此外,随着 t t t 的增加,梯度逐渐减小。因此, σ σ σ 值在演化的早期阶段急剧下降,而在演化的后期阶段只有轻微的下降。这样,在早期阶段扩展较大,以加速收敛到 CPF,但在后期阶段扩展较小,以确保 CPF 的开发能力。

3)分析: 为了分析CCSO的搜索行为,两个 artificial scenarios 如图 4 所示。
- 1) 图 4 (a) 描绘了 loser solution x l x_l xl?向 winner solution x w x_w xw?学习的搜索轨迹。根据扩展因子σ, x l x_l xl?可以超过 x w x_w xw?,因为 σ r 1 Δ ′ \sigma r_1\Delta^{\prime} σr1?Δ′ 大于 r 1 Δ ′ r_1\Delta^{\prime} r1?Δ′。此外,随着σ的减小,延伸量也随之减小。因此,如果 x w x_w xw? 在后期近似 x b x_b xb?,则 x l x_l xl? 可以在 x w x_w xw? 附近搜索,以确保CPF的开发。
2)提出了协同群优化算法(Proposed Cooperative Swarm Optimizer): 对于协同群优化算法,基于算术交叉算子,粒子 x w x_w xw? 和 x l x_l xl? 的更新策略如下:
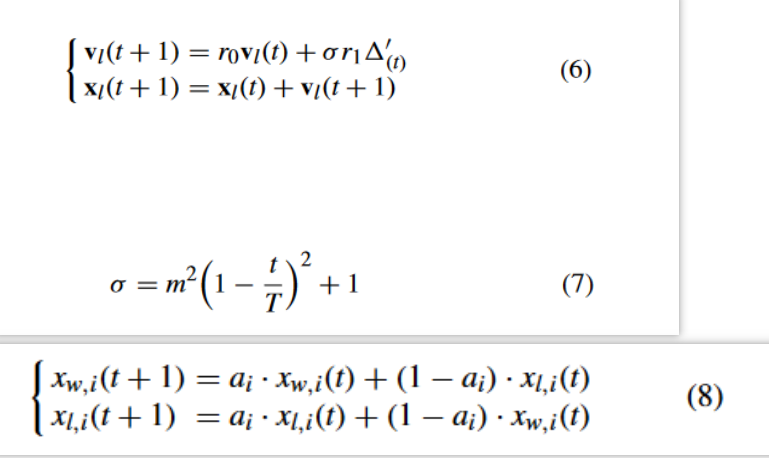
与上面原始 iCSO 的区别就在于:CCSO 协同群优化时,winner 也需要更新位置信息
2) 图 4 (b) 展示了两个解 x w x_w xw?和 x l x_l xl? 位于同一个非支配前沿的情形。With the cooperative swarm optimizer,产生了两个新的解[即 x w ( 1 ) x_{w(1)} xw(1)? 和 x l ( 1 ) x_{l(1)} xl(1)?] .因此,新产生的 winner solution x w ( 1 ) x_{w(1)} xw(1)? 能够跳出局部最优,更接近于 x b x_b xb?。
源码介绍
CMOPSO
classdef CMOCSO < ALGORITHM
% <multi> <real> <large/none> <constrained>
% Competitive and cooperative swarm optimization constrained multi-objective optimization algorithm
%------------------------------- Reference --------------------------------
% F. Ming, W. Gong, D. Li, L. Wang, and L. Gao, A competitive and
% cooperative swarm optimizer for constrained multi-objective optimization
% problems, IEEE Transactions on Evolutionary Computation, 2022.
%------------------------------- Copyright --------------------------------
% Copyright (c) 2023 BIMK Group. You are free to use the PlatEMO for
% research purposes. All publications which use this platform or any code
% in the platform should acknowledge the use of "PlatEMO" and reference "Ye
% Tian, Ran Cheng, Xingyi Zhang, and Yaochu Jin, PlatEMO: A MATLAB platform
% for evolutionary multi-objective optimization [educational forum], IEEE
% Computational Intelligence Magazine, 2017, 12(4): 73-87".
%--------------------------------------------------------------------------
% This function is written by Fei Ming
methods
function main(Algorithm,Problem)
%% Generate random population
Population = Problem.Initialization();
CV = sum(max(0,Population.cons),2);
CVmax = max(CV);
epsilon_0 = CVmax;
epsilon = epsilon_0;
Competitive_Pop = UpdateP1(Population,Problem.N,epsilon);
[Cooperative_Pop,Cooperative_Pop_Fitness] = UpdateP2(Population,Problem.N);
Population = UpdateP(Population,Problem.N);
Tc = 0.9 * ceil(Problem.maxFE/Problem.N);
cp = 2;
alpha = 0.95;
tao = 0.05;
y = 10;
G = Problem.maxFE/Problem.N;
%% Optimization
while Algorithm.NotTerminated(Population)
gen = ceil(Problem.FE/Problem.N); % 迭代次数
CV = sum(max(0,Competitive_Pop.cons),2); % 约束违反总数值
CV_max = max(CV);
CVmax = max([CV_max,CVmax]);
epsilon_0 = CVmax;
rf = sum(CV <= 1e-6) / length(Competitive_Pop);
epsilon = update_epsilon(tao,epsilon,epsilon_0,rf,alpha,gen,Tc,cp); % 利用 epsilon 约束处理技术更新 epsilon
Competitive_Pop_Fitness = CalFitness(Competitive_Pop.objs,Competitive_Pop.cons,epsilon);
if length(Competitive_Pop) >= 2
Rank = randperm(length(Competitive_Pop),floor(length(Competitive_Pop)/2)*2);
else
Rank = [1,1];
end
Loser = Rank(1:end/2);
Winner = Rank(end/2+1:end);
Change = Competitive_Pop_Fitness(Loser) <= Competitive_Pop_Fitness(Winner);
Temp = Winner(Change);
Winner(Change) = Loser(Change);
Loser(Change) = Temp;
Offspring1 = CompetitiveOperator(Problem,Competitive_Pop(Loser),Competitive_Pop(Winner),y);
LearningPool = TournamentSelection(2,Problem.N,Cooperative_Pop_Fitness);
Offspring2 = CooperativeOperator(Problem,Cooperative_Pop(LearningPool));
Offspring = [Offspring1,Offspring2];
Population = UpdateP([Population,Offspring],Problem.N);
Competitive_Pop = UpdateP1([Competitive_Pop,Offspring],Problem.N,epsilon);
gen = ceil(Problem.FE/Problem.N);
y = (Problem.M)^2*((gen/G)-1)^2+1;
[Cooperative_Pop,Cooperative_Pop_Fitness] = UpdateP2([Offspring,Cooperative_Pop],Problem.N);
end
end
end
end
function epsilon = update_epsilon(tao,epsilon_k,epsilon_0,rf,alpha,gen,Tc,cp)
% Update the value of epsilon
if gen > Tc
epsilon = 0;
else
if rf < alpha
epsilon = (1 - tao) * epsilon_k;
else
epsilon = epsilon_0 * ((1 - (gen / Tc)) ^ cp);
end
end
end
CV = sum(max(0, Population.cons), 2);
Population.cons是一个矩阵,包含了种群中每个个体的约束值(constraints)。每行对应一个个体,每列对应一个约束。max(0, Population.cons)将矩阵中的所有负值变为零。这是为了确保只考虑约束违规,忽略满足约束的情况。sum(..., 2)对每个个体的约束违规值进行求和,结果保存在向量CV中。每个元素CV(i)对应于种群中第i个个体的总约束违规值。
这行代码的目的是计算每个个体的约束违规总和,以便在后续的算法中使用这些值。如果某个个体的 CV 值为零,说明该个体在约束条件下是满足的。如果 CV 值大于零,表示个体在约束条件下存在违规。
UpdateP1
该函数用于选择满足特定约束的个体,具体来说是选择约束违规值小于给定阈值 epsilon 的个体。
function [Population,Fitness] = UpdateP1(Population,N,epsilon)
% Selecte epsilon feasible solutions
%------------------------------- Copyright --------------------------------
% Copyright (c) 2023 BIMK Group. You are free to use the PlatEMO for
% research purposes. All publications which use this platform or any code
% in the platform should acknowledge the use of "PlatEMO" and reference "Ye
% Tian, Ran Cheng, Xingyi Zhang, and Yaochu Jin, PlatEMO: A MATLAB platform
% for evolutionary multi-objective optimization [educational forum], IEEE
% Computational Intelligence Magazine, 2017, 12(4): 73-87".
%--------------------------------------------------------------------------
% This function is written by Fei Ming
%% Calculate the fitness of each solution
Fitness = CalFitness(Population.objs,Population.cons,epsilon);
%% Environmental selection
Next = Fitness < 1;
if sum(Next) < N
[~,Rank] = sort(Fitness);
Next(Rank(1:N)) = true;
elseif sum(Next) > N
Del = Truncation(Population(Next).objs,sum(Next)-N);
Temp = find(Next);
Next(Temp(Del)) = false;
end
% Population for next generation
Population = Population(Next);
end
function Del = Truncation(PopObj,K)
% Select part of the solutions by truncation
%% Truncation
Distance = pdist2(PopObj,PopObj);
Distance(logical(eye(length(Distance)))) = inf;
Del = false(1,size(PopObj,1));
while sum(Del) < K
Remain = find(~Del);
Temp = sort(Distance(Remain,Remain),2);
[~,Rank] = sortrows(Temp);
Del(Remain(Rank(1))) = true;
end
end
利用文章中的公式计算 fitness,详细见 CalFitness
Fitness = CalFitness(Population.objs,Population.cons, epsilon);
环境选择的步骤,用于选择下一代的种群
Next = Fitness < 1;
if sum(Next) < N
[~,Rank] = sort(Fitness);
Next(Rank(1:N)) = true;
elseif sum(Next) > N
Del = Truncation(Population(Next).objs,sum(Next)-N);
Temp = find(Next);
Next(Temp(Del)) = false;
end
Next = Fitness < 1;
Next是一个逻辑向量,其中Next(i)的值为true表示个体i的适应度小于1。
if sum(Next) < N
[~, Rank] = sort(Fitness);
Next(Rank(1:N)) = true;
- 如果适应度小于1的个体数量小于
N(种群大小),则选择适应度最小的前N个个体,确保至少有N个个体进入下一代。
elseif sum(Next) > N
Del = Truncation(Population(Next).objs, sum(Next) - N);
Temp = find(Next);
Next(Temp(Del)) = false;
- 如果适应度小于 1 的个体数量大于
N,则使用截断策略Truncation删除多余的个体。Truncation函数选择适应度较差的个体进行删除,确保最终种群大小为N。
% Population for next generation
Population = Population(Next);
- 最终,根据
Next的逻辑向量,选择满足条件的个体作为下一代的种群。
这样,Population 中保存的是被选择进入下一代的个体。这个环境选择的过程确保了下一代的种群符合适应度条件,并通过排序或截断操作来控制种群的大小。
CalFitness
该函数综合考虑了目标值之间的支配关系(R)和个体之间的距离(D),通过调整 epsilon 进行适应度的计算
1)选择: 算法 2 给出了"Selection() "过程。首先,将选择的 swarm P ′ \mathcal{P}^{'} P′ 初始化为空。那么, P \mathcal{P} P 中粒子的适应值根据如下计算:
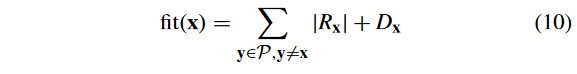
式中: R x R_x Rx? 表示可行性和收敛性评价,计算式为
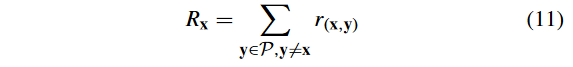
其中, r ( x , y ) r( x , y) r(x,y) 定义为
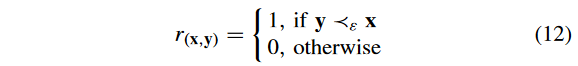
其中, y ? ε x y?_ε x y?ε?x 表示 y ? ε y~ ε y?ε-支配 x x x 。注意到,如果 ε = 0 ε = 0 ε=0,则 ? ε ?ε ?ε 作为CDP起作用;若 ε = ∞ ε =∞ ε=∞,则 ? ε ?ε ?ε 为传统的帕累托占优。
D x D_x Dx? 表示多样性的评价,计算为:
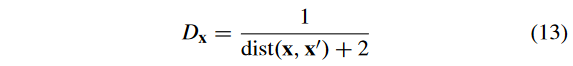
式中: d i s t ( x , x ′ ) dist( x , x^′) dist(x,x′) 为目标空间中 x x x 到 P \mathcal{P} P 的最近邻点的欧氏距离。这种适应度评价策略起源于 SPEA2 [36],已被证明在实现收敛性和多样性之间的平衡方面非常有效[37] [38]。
function Fitness = CalFitness(PopObj,PopCon,epsilon)
% Calculate the fitness of each solution based on different epsilon
%------------------------------- Copyright --------------------------------
% Copyright (c) 2023 BIMK Group. You are free to use the PlatEMO for
% research purposes. All publications which use this platform or any code
% in the platform should acknowledge the use of "PlatEMO" and reference "Ye
% Tian, Ran Cheng, Xingyi Zhang, and Yaochu Jin, PlatEMO: A MATLAB platform
% for evolutionary multi-objective optimization [educational forum], IEEE
% Computational Intelligence Magazine, 2017, 12(4): 73-87".
%--------------------------------------------------------------------------
% This function is written by Fei Ming
N = size(PopObj,1);
CV = sum(max(0,PopCon),2);
CV(CV < epsilon) = 0;
%% Detect the dominance relation between each two solutions
Dominate = false(N);
for i = 1 : N-1
for j = i+1 : N
if CV(i) < CV(j)
Dominate(i,j) = true;
elseif CV(i) > CV(j)
Dominate(j,i) = true;
else
k = any(PopObj(i,:)<PopObj(j,:)) - any(PopObj(i,:)>PopObj(j,:));
if k == 1
Dominate(i,j) = true;
elseif k == -1
Dominate(j,i) = true;
end
end
end
end
%% Calculate S(i)
S = sum(Dominate,2);
%% Calculate R(i)
R = zeros(1,N);
for i = 1 : N
R(i) = sum(S(Dominate(:,i)));
end
%% Calculate D(i)
Distance = pdist2(PopObj,PopObj);
Distance(logical(eye(length(Distance)))) = inf;
Distance = sort(Distance,2);
D = 1./(Distance(:,floor(sqrt(N)))+2);
%% Calculate the fitnesses
Fitness = R + D';
end
k = any(PopObj(i,:)<PopObj(j,:)) - any(PopObj(i,:)>PopObj(j,:));
if k == 1
Dominate(i,j) = true;
elseif k == -1
Dominate(j,i) = true;
end
-
PopObj(i,:)和PopObj(j,:)是两个不同个体的目标值向量。这里假设每个个体的目标值存储在矩阵PopObj的行中。 -
any(PopObj(i,:) < PopObj(j,:))返回一个逻辑值,表示是否存在至少一个目标值满足PopObj(i,:)小于PopObj(j,:)。 -
any(PopObj(i,:) > PopObj(j,:))返回一个逻辑值,表示是否存在至少一个目标值满足PopObj(i,:)大于PopObj(j,:)。 -
k的计算结果为:- 如果
PopObj(i,:)在所有目标值上都小于等于PopObj(j,:),则k为 1。 - 如果
PopObj(i,:)在所有目标值上都大于等于PopObj(j,:),则k为 -1。 - 如果存在某个目标值上
PopObj(i,:)小于PopObj(j,:)且存在某个目标值上PopObj(i,:)大于PopObj(j,:),则k为 0。
- 如果
这样,k 的值表示了个体 i 和个体 j 之间的支配关系:
k = 1表示个体i支配个体j。k = -1表示个体j支配个体i。k = 0表示个体i和个体j之间存在非支配关系。
计算每个个体的支配计数(S(i))。
S = sum(Dominate, 2);
Dominate是一个逻辑矩阵,其中Dominate(i, j)的值为true表示个体i支配个体j。sum(Dominate, 2)对Dominate矩阵的每一行进行求和,结果是一个列向量S,其中S(i)表示个体i被多少个其他个体支配。
因此,S(i) 表示个体 i 的支配计数,即有多少个个体支配了个体 i。在多目标优化问题中,支配计数常用于评估个体的 Pareto 支配强度。支配计数越小,个体越有可能位于 Pareto 前沿上。
这部分代码计算了每个个体的支配被计数(R(i))。
R = zeros(1, N);
for i = 1 : N
R(i) = sum(S(Dominate(:, i)));
end
-
S是一个列向量,其中S(i)表示个体i的支配计数,即有多少个个体支配了个体i。 -
Dominate(:, i)表示个体i是否支配其他个体的逻辑向量。Dominate(:, i)的第j个元素为true表示个体i支配个体j。 -
S(Dominate(:, i))选择了S中对应于个体i支配的个体的支配计数。 -
sum(S(Dominate(:, i)))对选中的支配计数进行求和,得到个体i的支配被计数R(i)。
因此,R(i) 表示个体 i 的支配被计数,即有多少个个体被个体 i 支配。在多目标优化问题中,支配被计数用于评估个体在 Pareto 前沿上的拥挤度。支配被计数越小,个体在 Pareto 前沿上的拥挤度越高。
这部分代码计算了每个个体之间的距离(D)。让我为您解释这段代码的具体含义:
Distance = pdist2(PopObj, PopObj);
Distance(logical(eye(length(Distance)))) = inf;
Distance = sort(Distance, 2);
D = 1./(Distance(:, floor(sqrt(N))) + 2);
-
pdist2(PopObj, PopObj)计算了种群中每两个个体之间的距离。结果矩阵Distance是一个对称矩阵,其中Distance(i, j)表示个体i和个体j之间的欧氏距离。 -
logical(eye(length(Distance)))创建了一个对角线上元素为逻辑值true的单位矩阵,表示每个个体与自身的距离为无穷大。 -
Distance(logical(eye(length(Distance)))) = inf;将对角线上的距离设置为无穷大,排除了个体与自身的距离。 -
sort(Distance, 2)对Distance矩阵的每一行进行升序排序,结果矩阵Distance中的每一行都包含了个体到其他个体的距离,按照距离的增序排列。 -
Distance(:, floor(sqrt(N)))取每一行的前floor(sqrt(N))个距离。 -
1./(Distance(:, floor(sqrt(N))) + 2)计算每个个体到其最近邻的距离的倒数,加上一个小的常数 2 防止除零错误。这样得到的向量D表示了每个个体到其最近邻的距离的逆。
因此,D(i) 表示个体 i 到其最近邻的距离的逆。在多目标优化问题中,这样的距离度量通常用于评估个体在 Pareto 前沿上的分布密度。
UpdateP2
function [Population,Fitness] = UpdateP1(Population,N,epsilon)
% Selecte epsilon feasible solutions
%------------------------------- Copyright --------------------------------
% Copyright (c) 2023 BIMK Group. You are free to use the PlatEMO for
% research purposes. All publications which use this platform or any code
% in the platform should acknowledge the use of "PlatEMO" and reference "Ye
% Tian, Ran Cheng, Xingyi Zhang, and Yaochu Jin, PlatEMO: A MATLAB platform
% for evolutionary multi-objective optimization [educational forum], IEEE
% Computational Intelligence Magazine, 2017, 12(4): 73-87".
%--------------------------------------------------------------------------
% This function is written by Fei Ming
%% Calculate the fitness of each solution
Fitness = CalFitness(Population.objs,Population.cons, epsilon);
%% Environmental selection
Next = Fitness < 1;
if sum(Next) < N
[~,Rank] = sort(Fitness);
Next(Rank(1:N)) = true;
elseif sum(Next) > N
Del = Truncation(Population(Next).objs,sum(Next)-N);
Temp = find(Next);
Next(Temp(Del)) = false;
end
% Population for next generation
Population = Population(Next);
end
function Del = Truncation(PopObj,K)
% Select part of the solutions by truncation
%% Truncation
Distance = pdist2(PopObj,PopObj);
Distance(logical(eye(length(Distance)))) = inf;
Del = false(1,size(PopObj,1));
while sum(Del) < K
Remain = find(~Del);
Temp = sort(Distance(Remain,Remain),2);
[~,Rank] = sortrows(Temp);
Del(Remain(Rank(1))) = true;
end
end
这个函数的逻辑与之前的 UpdateP1 函数类似,但有一些关键差异:
-
Fitness的计算: 这里使用了
CalFitness函数,其中inf作为epsilon参数。这将导致计算每个解的适应度时忽略了约束违规值。 -
环境选择: 环境选择的逻辑仍然是根据适应度值进行的。首先,选择适应度小于1的解。如果数量不足N,就选择适应度最小的前N个解。如果数量超过N,就使用截断策略
Truncation删除一些解以保持数量为N。 -
返回结果: 返回的是选择后的种群
Population和对应的适应度值Fitness。
这个函数的作用是在种群中选择非支配解,以用于协作操作。非支配解是 Pareto 前沿上的解,它们相互之间不存在支配关系。
UpdateP
function Population = UpdateP(Population,N)
% Select feasible and non-dominated solutions
%------------------------------- Copyright --------------------------------
% Copyright (c) 2023 BIMK Group. You are free to use the PlatEMO for
% research purposes. All publications which use this platform or any code
% in the platform should acknowledge the use of "PlatEMO" and reference "Ye
% Tian, Ran Cheng, Xingyi Zhang, and Yaochu Jin, PlatEMO: A MATLAB platform
% for evolutionary multi-objective optimization [educational forum], IEEE
% Computational Intelligence Magazine, 2017, 12(4): 73-87".
%--------------------------------------------------------------------------
% This function is written by Fei Ming
%% Select feasible solutions
fIndex = all(Population.cons <= 0,2);
Population = Population(fIndex);
if isempty(Population)
return
elseif length(Population)>N
Fitness = CalFitness(Population.objs,Population.cons,0);
Next = Fitness < 1;
Del = Truncation(Population(Next).objs,sum(Next)-N);
Temp = find(Next);
Next(Temp(Del)) = false;
Population = Population(Next);
end
end
function Del = Truncation(PopObj,K)
% Select part of the solutions by truncation
%% Truncation
Distance = pdist2(PopObj,PopObj);
Distance(logical(eye(length(Distance)))) = inf;
Del = false(1,size(PopObj,1));
while sum(Del) < K
Remain = find(~Del);
Temp = sort(Distance(Remain,Remain),2);
[~,Rank] = sortrows(Temp);
Del(Remain(Rank(1))) = true;
end
end
fIndex = all(Population.cons <= 0,2);
使用逻辑条件 Population.cons <= 0 来检查种群中每个个体的约束是否都小于等于0,然后使用 all(..., 2) 对每行进行逻辑 AND 操作,得到一个逻辑向量 fIndex。这个向量的每个元素 fIndex(i) 表示种群中第 i 个个体是否满足所有约束条件。
因此,fIndex(i) 为 true 表示第 i 个个体的所有约束都满足(都小于等于0),而 false 表示有至少一个约束不满足。在这种情况下,fIndex 将用于筛选满足约束条件的个体。
Tc = 0.9 * ceil(Problem.maxFE/Problem.N);
cp = 2;
alpha = 0.95;
tao = 0.05;
y = 10;
G = Problem.maxFE/Problem.N;
注: 这里的 y 就是文章中的 σ σ σ
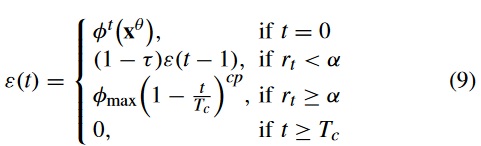
-
cp:这个参数控制了epsilon更新的方式中的幂指数。在epsilon更新的公式中,cp用于计算(gen/Tc)^cp。cp的值为 2。 -
alpha:这个参数用于epsilon更新的条件判断。在epsilon更新的公式中,如果rf(无约束的个体比例)小于alpha,则使用(1 - tao) * epsilon_k进行更新,否则使用epsilon_0 * ((1 - (gen / Tc))^cp)进行更新。alpha的值为 0.95。 -
tao:这是一个权衡因子,用于在epsilon更新时对当前epsilon进行调整的比例。在epsilon更新的公式中,如果rf小于alpha,则使用(1 - tao) * epsilon_k进行更新。tao的值为 0.05。 -
y:这个参数用于计算协作操作中的某个权重值。在代码中,它与(Problem.M)^2*((gen/G)-1)^2+1一起计算协作操作中的某个参数。y的值为 10。 -
G:这个参数用于计算协作操作中的某个权重值。在代码中,它与(Problem.M)^2*((gen/G)-1)^2+1一起计算协作操作中的某个参数。G的值为Problem.maxFE/Problem.N,表示总评估次数除以种群大小,用于计算当前进化代数相对于总评估次数的比例。
main
这一行代码计算了无约束的个体比例 rf。让我为您解释一下:
rf = sum(CV <= 1e-6) / length(Competitive_Pop);
-
CV是一个列向量,其中CV(i)表示第i个个体的约束违规值。 -
CV <= 1e-6产生一个逻辑向量,其中CV(i) <= 1e-6的元素为true,否则为false。这表示约束违规值小于等于1e-6的个体。 -
sum(CV <= 1e-6)对逻辑向量进行求和,得到约束违规值小于等于1e-6的个体的数量。 -
length(Competitive_Pop)得到当前竞争种群的大小,即个体的数量。 -
因此,
sum(CV <= 1e-6) / length(Competitive_Pop)计算了约束违规值小于等于1e-6的个体在竞争种群中的比例,即无约束的个体比例rf。
update_epsilon
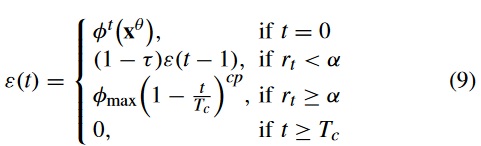
function epsilon = update_epsilon(tao,epsilon_k,epsilon_0,rf,alpha,gen,Tc,cp)
% Update the value of epsilon
if gen > Tc
epsilon = 0;
else
if rf < alpha
epsilon = (1 - tao) * epsilon_k;
else
epsilon = epsilon_0 * ((1 - (gen / Tc)) ^ cp);
end
end
end
用于后续在竞争种群中选择个体进行竞争操作。
if length(Competitive_Pop) >= 2
Rank = randperm(length(Competitive_Pop), floor(length(Competitive_Pop) / 2) * 2);
else
Rank = [1, 1];
end
-
length(Competitive_Pop)得到当前竞争种群的大小,即个体的数量。 -
floor(length(Competitive_Pop) / 2) * 2计算了最接近且小于竞争种群大小的偶数。 -
randperm(length(Competitive_Pop), ...)生成一个包含长度为竞争种群大小的随机排列的向量。 -
因为在某些情况下,竞争种群大小可能不是偶数,所以使用
floor函数将其调整为偶数,以确保后续的竞争操作可以正确进行。 -
如果竞争种群的大小大于等于2,那么
Rank就是一个包含两两竞争个体索引的随机排列。如果竞争种群大小小于2,那么Rank就是一个包含两个相同索引值的向量[1, 1],这样可以确保至少有两个索引值用于后续的竞争操作。
CompetitiveOperator
function Offspring = CompetitiveOperator(Problem,Loser,Winner,y)
% The competitive swarm optimizer
%------------------------------- Copyright --------------------------------
% Copyright (c) 2023 BIMK Group. You are free to use the PlatEMO for
% research purposes. All publications which use this platform or any code
% in the platform should acknowledge the use of "PlatEMO" and reference "Ye
% Tian, Ran Cheng, Xingyi Zhang, and Yaochu Jin, PlatEMO: A MATLAB platform
% for evolutionary multi-objective optimization [educational forum], IEEE
% Computational Intelligence Magazine, 2017, 12(4): 73-87".
%--------------------------------------------------------------------------
% This function is written by Fei Ming
%% Parameter setting
LoserDec = Loser.decs;
WinnerDec = Winner.decs;
[N,D] = size(LoserDec);
LoserVel = Loser.adds(zeros(N,D));
WinnerVel = Winner.adds(zeros(N,D));
%% Competitive swarm optimizer
r1 = repmat(rand(N,1),1,D);
r2 = repmat(rand(N,1),1,D);
OffVel = r1.*LoserVel + r2.*(WinnerDec-LoserDec)*y;
n = randi(2,1,1);
OffDec = LoserDec + OffVel + r1.*(OffVel-LoserVel)*(-1)^n;
%% Add the winners
OffDec = [OffDec;WinnerDec];
OffVel = [OffVel;WinnerVel];
%% Polynomial mutation
Lower = repmat(Problem.lower,2*N,1);
Upper = repmat(Problem.upper,2*N,1);
disM = 20;
Site = rand(2*N,D) < 1/D;
mu = rand(2*N,D);
temp = Site & mu<=0.5;
OffDec = max(min(OffDec,Upper),Lower);
OffDec(temp) = OffDec(temp)+(Upper(temp)-Lower(temp)).*((2.*mu(temp)+(1-2.*mu(temp)).*...
(1-(OffDec(temp)-Lower(temp))./(Upper(temp)-Lower(temp))).^(disM+1)).^(1/(disM+1))-1);
temp = Site & mu>0.5;
OffDec(temp) = OffDec(temp)+(Upper(temp)-Lower(temp)).*(1-(2.*(1-mu(temp))+2.*(mu(temp)-0.5).*...
(1-(Upper(temp)-OffDec(temp))./(Upper(temp)-Lower(temp))).^(disM+1)).^(1/(disM+1)));
Offspring = Problem.Evaluation(OffDec,OffVel);
end
CooperativeOperator
function Offspring = CooperativeOperator(Problem,Parent,Parameter)
% The cooperative swarm optimizer based on GA formula
%------------------------------- Copyright --------------------------------
% Copyright (c) 2023 BIMK Group. You are free to use the PlatEMO for
% research purposes. All publications which use this platform or any code
% in the platform should acknowledge the use of "PlatEMO" and reference "Ye
% Tian, Ran Cheng, Xingyi Zhang, and Yaochu Jin, PlatEMO: A MATLAB platform
% for evolutionary multi-objective optimization [educational forum], IEEE
% Computational Intelligence Magazine, 2017, 12(4): 73-87".
%--------------------------------------------------------------------------
% This function is written by Fei Ming
%% Parameter setting
if nargin > 2
[proC,disC,proM,disM] = deal(Parameter{:});
else
[proC,disC,proM,disM] = deal(1,20,1,20);
end
if isa(Parent(1),'SOLUTION')
calObj = true;
Parent = Parent.decs;
else
calObj = false;
end
Parent1 = Parent(1:floor(end/2),:);
Parent2 = Parent(floor(end/2)+1:floor(end/2)*2,:);
[N,D] = size(Parent1);
%% Genetic operators for real encoding
% Simulated binary crossover
beta = zeros(N,D);
mu = rand(N,D);
beta(mu<=0.5) = (2*mu(mu<=0.5)).^(1/(disC+1));
beta(mu>0.5) = (2-2*mu(mu>0.5)).^(-1/(disC+1));
beta = beta.*(-1).^randi([0,1],N,D);
beta(rand(N,D)<0.5) = 1;
beta(repmat(rand(N,1)>proC,1,D)) = 1;
Offspring = [(Parent1+Parent2)/2+beta.*(Parent1-Parent2)/2
(Parent1+Parent2)/2-beta.*(Parent1-Parent2)/2];
% Polynomial mutation
Lower = repmat(Problem.lower,2*N,1);
Upper = repmat(Problem.upper,2*N,1);
Site = rand(2*N,D) < proM/D;
mu = rand(2*N,D);
temp = Site & mu<=0.5;
Offspring = min(max(Offspring,Lower),Upper);
Offspring(temp) = Offspring(temp)+(Upper(temp)-Lower(temp)).*((2.*mu(temp)+(1-2.*mu(temp)).*...
(1-(Offspring(temp)-Lower(temp))./(Upper(temp)-Lower(temp))).^(disM+1)).^(1/(disM+1))-1);
temp = Site & mu>0.5;
Offspring(temp) = Offspring(temp)+(Upper(temp)-Lower(temp)).*(1-(2.*(1-mu(temp))+2.*(mu(temp)-0.5).*...
(1-(Upper(temp)-Offspring(temp))./(Upper(temp)-Lower(temp))).^(disM+1)).^(1/(disM+1)));
if calObj
Offspring = Problem.Evaluation(Offspring);
end
end
这几行代码用于将输入的父代个体 (Parent) 分成两部分,即 Parent1 和 Parent2。这两个部分将用于后续的遗传算法操作。以下是这几行代码的解释:
Parent1 = Parent(1:floor(end/2), :);
Parent2 = Parent(floor(end/2) + 1:floor(end/2) * 2, :);
[N, D] = size(Parent1);
-
floor(end/2)计算了父代个体数量的一半,向下取整。这用于确定从父代中选择的个体数量。 -
Parent(1:floor(end/2), :)选择了父代的前一半个体,存储在Parent1中。 -
Parent(floor(end/2) + 1:floor(end/2) * 2, :)选择了父代的后一半个体,存储在Parent2中。 -
size(Parent1)得到了Parent1的大小,即选择的个体数量N和个体的维度D。
这样,Parent1 和 Parent2 就分别包含了父代的前一半和后一半个体,用于进行遗传算法的交叉和变异操作。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 在做题中学习(43):长度最小的子数组
- Transmit:连接文件传输的极致之选
- 第一章. HTML 与 CSS
- js实现点击音频实现播放功能
- 实践案例分享|广发证券——夯实数据底座,赋能敏捷场景
- Java基础- 泛型
- 向量表示在自然语言、知识图谱和图像视觉中的应用
- 剪板机丝杆的维护保养方法
- 【INTEL(ALTERA)】错误:altera_axi4lite_slave:缺少必需信号:awprot、arprot怎么办
- KNN与KD树博客总结