MiniTab的拟合回归模型的分析

拟合回归模型概述

使用拟合回归模型和普通最小二乘法可以描述一组预测变量和一个连续响应之间的关系。可以包括交互作用项和多项式项、执行逐步回归和变换偏斜数据。

例如，房地产评估人员想了解城市公寓与多个预测变量（包括建筑面积、可用单元数量、建筑年限和到市中心的距离）之间的相关性。检验员可以使用多个回归来确定预测变量是否与销售价格显著相关。

在执行分析之后，Minitab 将存储模型，以便执行如下操作：

• 预测新观测值的响应。
• 绘制变量之间的关系图。
• 查找对一个或多个响应进行优化的值。

菜单位置：统计?> 回归?> 回归?> 拟合回归模型。

何时使用备择分析

• 如果标绘一个连续（数值）预测变量和一个连续响应之间的关系，请使用 拟合线图。
• 如果具有嵌套或随机的类别预测变量，则在具有所有固定因子时使用拟合一般线性模型，或在具有随机因子时使用拟合混合效应模型。
• 如果的响应变量有两个类别（如通过和失败），请使用拟合二元 Logistic 模型。
• 如果的响应变量包含三个或更多采用一定自然顺序的类别（如非常不同意、不同意、中立、同意和非常同意），请使用顺序 Logistic 回归。
• 如果的响应变量包含三个或更多不采用自然顺序的类别（如擦痕、凹陷和撕裂），请使用名义 Logistic 回归。
• 如果的响应变量对发生次数（如缺陷数量）进行计数，请使用拟合 Poisson 模型。

数据注意事项

为了确保结果有效，收集数据、执行分析和解释结果时考虑以下5个准则。

1、预测变量可以是连续变量或类别变量

连续变量可以测量和排序，它可以拥有介于两个值之间的无限数量的值。例如，轮胎样本的直径是连续变量。

类别变量包含有限、可计数的类别数或可区分组数。类别数据可能不是逻辑顺序。例如，类别变量包括性别、材料类型和付款方式。

如果有离散变量，则可以决定是将它视为连续预测变量还是类别预测变量。离散变量可以进行测量和排序，但是它具有可计数的值。例如，家庭成员数是离散变量。可根据水平数以及分析的目的来决定将离散变量视为连续变量还是类别变量。

• 如果标绘一个连续（数值）预测变量和一个连续响应之间的关系，请使用 拟合线图。
• 如果具有嵌套或随机的类别预测变量，则在具有所有固定因子时使用?拟合一般线性模型，或在具有随机因子时使用?拟合混合效应模型。

2、响应变量应当是连续变量

如果响应变量是类别变量，则的模型不太可能满足分析假定、准确描述数据或者进行有用的预测。

• 如果的响应变量有两个类别（如通过和失败），请使用?拟合二元 Logistic 模型。
• 如果的响应变量包含三个或更多采用一定自然顺序的类别（如非常不同意、不同意、中立、同意和非常同意），请使用?顺序 Logistic 回归。
• 如果的响应变量包含三个或更多不采用自然顺序的类别（如擦痕、凹陷和撕裂），请使用?名义 Logistic 回归。
• 如果的响应变量对发生次数（如缺陷数量）进行计数，请使用?拟合Poisson模型。

3、使用最佳做法收集数据

要确保结果有效，请考虑以下准则：

• 确保数据代表感兴趣的总体。
• 收集足够多的数据以提供必要的精确度。
• 尽可能准确和精确地测量变量。
• 以数据的收集顺序记录数据。

4、预测变量之间的相关性（又称为多重共线性）应当不严重

如果多重共线性严重，则可能无法确定要在模型中包括哪些预测变量。要确定多重共线性的严重性，请使用输出的“系数”表格中的方差膨胀因子 (VIF)。

5、模型应当提供良好的数据拟合

如果模型无法与数据拟合，则结果可能会具有误导性。在输出中，使用残值图、异常观测值的诊断统计量以及模型汇总统计量可以确定模型对数据的拟合优度。

拟合回归模型示例

研究化学家想要了解多个预测变量与棉布抗皱性的关联性。化学家检查 32 件在不同的凝固时间、凝固温度、甲醛浓度和催化剂比率下生产出的棉纤维素。对每件棉布都记录了耐压等级（用来度量抗皱性）。

浓度	比率	温度	时间	评级
8	4	100	1	1.4
2	4	180	7	2.25
7	4	180	1	4.6
10	7	120	5	4.9
7	4	180	5	4.6
7	7	180	1	4.75
7	13	140	1	4.6
5	4	160	7	4.5
4	7	140	3	4.8
5	1	100	7	1.4
8	10	140	3	4.7
2	4	100	3	1.6
4	10	180	3	4.5
6	7	120	7	4.7
10	13	180	3	4.8
4	10	160	5	4.6
4	13	100	7	4.3
10	10	120	7	4.9
5	4	100	1	1.7
8	13	140	1	4.6
10	1	180	1	2.6
2	13	140	1	3.1
6	13	180	7	4.7
7	1	120	7	2.5
5	13	140	1	4.5
8	1	160	7	2
4	1	180	7	1.8
6	1	160	1	1.5
4	1	100	1	1.3
7	10	100	7	4.6
4	1	100	1	1.4
4	1	100	1	1.45

参数设置如下图：

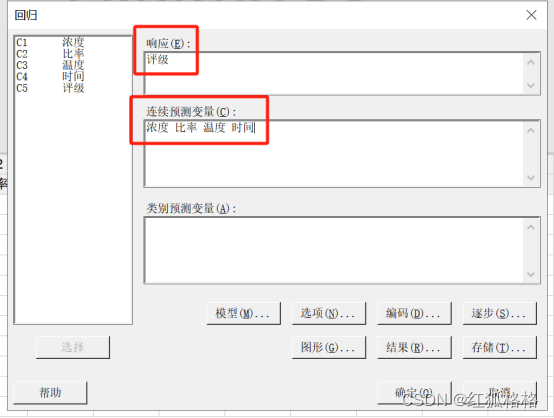
“图形”设置如下图：

主要结果分析

作为预测变量的温度、催化剂比率和甲醛浓度的 p 值小于显著水平 0.05。这些结果表示这些预测变量对抗皱性具有统计意义上非常显著的效应。时间的 p 值大于 0.05，这表示没有足够的证据可以断定时间与响应相关。化学家可能需要重新拟合不具有此预测变量的模型。

Pareto 图显示在显著性水平为 0.05 时，温度、催化剂比率和甲醛浓度的效应在统计意义上显著。最大的效应是催化剂比率，因为它延伸得最远。最小的效应是时间效应，因为它延伸得最近。

此残差图指示该模型可能有问题。

• 残差与拟合值图中的点并未随机分布在零附近。但似乎存在表示不同数据组的点群集。化学家应该研究这些组以确定其原因。
• 残差与比率图显示了弯曲，这表明催化剂比率与皱纹之间具有曲线关系。化学家应该考虑向该模型添加比率的二次项。

关键输出包括 p 值、系数、R2 及残差图。

步骤 1：确定哪些项对响应变异性的贡献最大

使用 Pareto 效应图可比较项的相对量值与统计显著性。该图在模型保留误差的自由度时显示。

Minitab 按照项的绝对值的递减顺序为这些项绘图。图中的参考线表明哪些项是显著项。默认情况下，Minitab 使用显著性水平 0.05 绘制参考线。

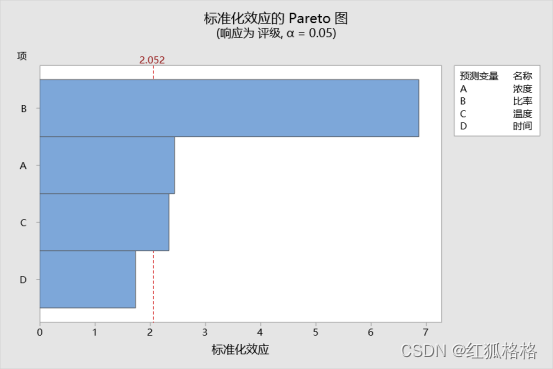
主要结果：Pareto 图

在这些结果中，3 个项的效应在统计意义上显著 (α = 0.05)。显著效应为甲醛浓度 (A)、催化剂比率 (B) 和温度 (C)。时间效应 (D) 在统计意义上不显著，因为该条形未延伸出红线。

最大的效应是催化剂比率 (B)，因为该条形延伸得最远。时间效应 (D) 为最小效应，因为该条形延伸得最近。

步骤 2：确定响应变量和项之间的关联在统计意义上是否显著

要确定响应与模型中每个项之间的关联在统计意义上是否显著，请将该项的 P 值与显著性水平进行比较以评估原假设。原假设声明该项与响应之间没有关联。通常，显著性水平（用 α 或 alpha 表示）为 0.05 即可。显著性水平 0.05 指示在实际上不存在关联时得出存在关联的风险为 5%。

P 值 ≤ α：关联在统计意义上显著

如果 P 值小于或等于显著性水平，则可以得出响应变量与项之间的关联在统计意义上显著的结论。

P 值 > α：关联在统计意义上不显著

如果 p 值大于显著性水平，则无法得出响应变量与该项之间的关联在统计意义上显著的结论。可能希望重新拟合没有该项的模型。

如果多个预测变量与响应在统计意义上没有显著的关联，则可以通过删除项（一次删除一个）来简化模型。

如果一个模型项在统计意义上显著，则解释取决于该项的类型。解释如下所示：

• 如果一个连续预测变量显著，则可以得出该预测变量的系数不等于零的结论。
• 如果一个类别预测变量显著，则可以断定并非所有水平均值都相等。
• 如果一个交互作用项显著，则一个因子与响应之间的关系取决于该项中的其他因子。
• 如果一个多项式项显著，则可以得出数据包含弯曲的结论。

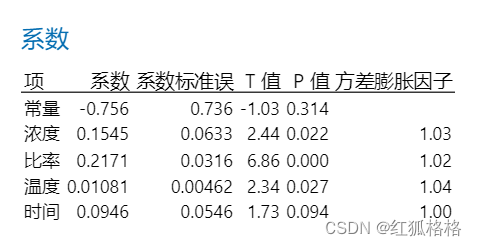
主要结果：P 值、系数

甲醛浓度、催化剂比率和温度等预测变量的?P 值小于显著水平 .05。这些结果表示这些预测变量与抗皱性之间存在统计上非常显著的关系。例如，甲醛浓度系数估计浓度每增加一个单位，抗皱性平均值增加 .1545 个单位，而模型中的其他项保持恒定。

时间的 P 值大于 .05，这表示没有足够的证据可以断定时间与响应变量相关。化学家可能需要重新拟合不具有此预测变量的模型。

步骤 3：确定模型对数据的拟合优度

要确定模型与数据的拟合优度，请检查模型汇总表中的拟合优度统计量。

S：使用 S 可评估模型描述响应值的程度。使用 S 替代 R2 统计量，以比较不具有常量的模型拟合。

S 以响应变量的单位进行度量，它表示数据值与拟合值的距离。S 值越低，模型描述响应的程度越高。但是，自身低 S 值并不表明模型符合模型假设。应检查残差图来验证假设。

R-sq：R2 值越高，模型拟合数据的优度越高。R2 始终介于 0% 和 100% 之间。

如果向模型添加其他预测变量，则 R2 会始终增加。例如，最佳的 5 预测变量模型的 R2 始终比最佳的 4 预测变量模型的高。因此，比较相同大小的模型时 R2 最有效。

R-sq（调整）：在想要比较具有不同数量的预测变量的情况下，使用调整的 R2。如果向模型添加预测变量，即使模型没有实际改善，R2 也会始终增加。调整的 R2 值包含模型中的预测变量数，以便帮助选择正确的模型。

R-sq（预测）：使用预测的 R2 可确定模型对新观测值的响应进行预测的程度。具有较大预测 R2 值的模型的预测能力也较出色。

实质上，小于 R2 的预测的 R2 可能表明模型过度拟合。在向总体中添加不太重要的影响项的情况下，可能会发生过度拟合模型。模型针对样本数据而定制，因此可能对于总体预测不太有效。

在比较模型方面，预测的 R2 还可能比调整的 R2?更有效，因为它是用模型计算中未包含的观测值计算得出的。

AICc 和 BIC：当显示逐步方法每个步骤的详细信息时或者显示分析的扩展结果时，Minitab 会多显示两个统计量。这些统计量是更正的 Akaike 信息标准 (AICc) 和 Bayesian 信息标准 (BIC)。使用这些统计量可以比较不同的模型。对于每个统计量，较小的值比较合意。

解释拟合优度统计量时，请考虑以下几点：

1. 样本数量较小则不能提供对于响应变量和预测变量之间关系强度的精确估计。如果需要 R2 更为精确，则应当使用较大的样本（通常为 40 或更多）。
2. 拟合优度统计量只是模型拟合数据优度的一种度量。即使模型具有合意的值，也应当检查残差图，以验证模型是否符合模型假设。

?

主要结果：S、R-sq、R-Sq（调整）、R-Sq（预测）

在这些结果中，模型可以解释响应变量中约 73% 的变异。对于这些数据，R2 值表示模型与数据充分拟合。如果要拟合具有不同预测变量的其他模型，请使用调整的 R2 值和预测的 R2 值比较模型与数据的拟合。

步骤 4：确定模型是否符合分析的假设条件

使用残差图可帮助确定模型是否适用并符合分析的假设。如果不符合此假设，则模型可能无法充分拟合数据，在解释结果时应当格外小心。

残差与拟合值图

使用残差与拟合值图可验证残差随机分布和具有常量方差的假设。理想情况下，点应当在 0 的两端随机分布，点中无可辨识的模式。

下表中的模式可能表示该模型不满足模型假设。

模式	模式的含义
残差相对拟合值呈扇形或不均匀分散	异方差
曲线	缺少高阶项
远离 0 的点	异常值
在 X 方向远离其他点的点	有影响的点

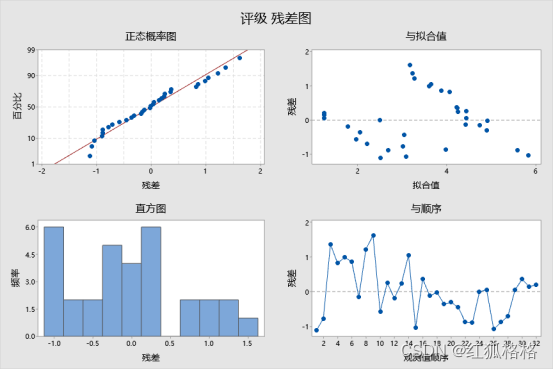
此残差与拟合值图中的点并未随机分布在零附近。但似乎存在表示不同数据组的点群集。应该研究这些组以确定其原因。

?

残差与顺序图

使用残差与顺序图可验证残差独立于其他残差的假设。当以时序显示时，独立残差不显示趋势或模式。点中的模式可能表明，彼此相近的残差可能相关联，因此并不独立。理想情况下，图中的残差应围绕中心线随机分布：

残差与顺序图

使用残差与顺序图可验证残差独立于其他残差的假设。当以时序显示时，独立残差不显示趋势或模式。点中的模式可能表明，彼此相近的残差可能相关联，因此并不独立。理想情况下，图中的残差应围绕中心线随机分布：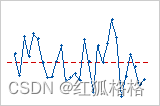

如果查看模式，便可查出原因。下列类型的模式可能表明残差属于依赖项。

趋势：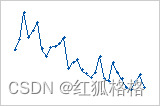

偏移：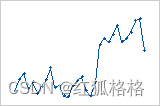

周期：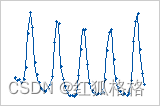

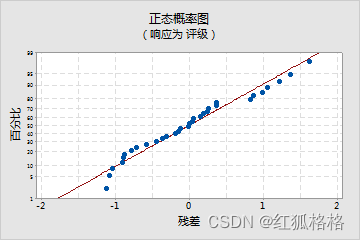
残差的正态概率图

使用残差正态概率图可验证残差呈正态分布的假设。残差的正态概率图应该大致为一条直线。

下表中的模式可能表示该模型不满足模型假设。

模式	模式的含义
非直线	非正态性
远离直线的点	异常值
斜率不断变化	未确定的变量

在此正态概率图中，点通常为一条直线。没有证据表明存在非正态性、异常值或未确定的变量。

Tips：为拟合回归模型存储统计量

统计?> 回归?> 回归?> 拟合回归模型?> 存储

可以将分析统计量保存到工作表中，以便可以将它们用在其他分析、图形和宏中。Minitab 将选定的统计量存储在最后一个数据列后面。存储列的名称以一个数字结尾，如果将同一个统计量存储多次，结尾的数字会递增。

可以存储的统计量

1. 拟合：Minitab 将拟合值存储在 FITS 列中。
2. 残差：Minitab 将残差存储在 RESI 列中。
3. 标准化残差：Minitab 将标准化残差存储在 SRES 列中。
4. 删后残差：Minitab 将删后残差存储在 TRES 列中。
5. 杠杆率：Minitab 将杠杆率存储在 HI 列中。
6. Cook 距离：Minitab 将 Cook 距离存储在 COOK 列中。
7. DFITS：Minitab 将 DFITS 存储在 DFIT 列中。
8. 系数：Minitab 将系数存储在 COEF 列中。
9. 设计矩阵：Minitab 将设计矩阵存储在名为 XMAT 的矩阵中。要查看矩阵，请选择数据?> 显示数据。要将矩阵复制到工作表，请选择数据?> 复制?> 矩阵到列。
10. Box-Cox 变换：如果要变换响应变量，可以存储有关变换的信息。
11. 响应的 Box-Cox 变换：Minitab 将响应的变换值存储在 BCRESP 列中。
12. 原始响应的拟合：Minitab 将原始响应的拟合值存储在 BFITS 列中。