AI模型部署基础知识(一):模型权重与参数精度
一般情况来说,我们通过收集数据,训练深度学习模型,通过反向传播求导更新模型的参数,得到一个契合数据和任务的模型。这一阶段,通常使用python&pytorch进行模型的训练得到pth等类型文件。AI模型部署就是将在python环境中训练的模型参数放到需要部署的硬件环境中去跑,比如云平台和其他cpu、gpu设备中。一般来说,权重信息以及权重分布基本不会变(可能会改变精度、也可能会合并一些权重)。
该部分笔记参考oldpan内容
模型权重
一般我们使用Pytorch模型进行训练。训练得到的权重,我们一般都会使用torch.save()保存为.pth的格式。
pth文件内容
pth是Pytorch使用python中内置模块pickle来保存和读取,pth文件的中主要包含字符段{‘epoch’: 190, ‘state_dict’: OrderedDict([(‘conv1.weight’, tensor([[…,},其中epoch 为pth保存的轮次数、state_dict中包含主要的模型结构名称和对应模型参数值,
state_dict的key:

- 主要权重结构
在模型训练过程中,有很多需要通过反向传播更新的权重,常见的有:
卷积层(conv.weight \conv.bias)
全连接层 (fc.weight)
批处理化层(BN层、或者各种其他LN、IN、GN)
transformer-encoder层
DCN层
这些层一般都是神经网络的核心部分,当然都是有参数的,一定会参与模型的反向传播更新,是我们在训练模型时候需要注意的重要参数。
- BN的反向传播与参数更新
BN层中的可学习参数(如果affine=True)会参与反向传播并在训练过程中更新,而用于归一化的统计量(running_mean和running_var)则通过不同的机制进行更新。
# 截取了Pytorch中BN层的部分代码
def __init__(
self,
num_features: int,
eps: float = 1e-5,
momentum: float = 0.1,
affine: bool = True,
track_running_stats: bool = True
) -> None:
super(_NormBase, self).__init__()
self.num_features = num_features
self.eps = eps
self.momentum = momentum
self.affine = affine
self.track_running_stats = track_running_stats
if self.affine:
self.weight = Parameter(torch.Tensor(num_features))
self.bias = Parameter(torch.Tensor(num_features))
else:
self.register_parameter('weight', None)
self.register_parameter('bias', None)
if self.track_running_stats:
# 可以看到在使用track_running_stats时,BN层会更新这三个参数
self.register_buffer('running_mean', torch.zeros(num_features))
self.register_buffer('running_var', torch.ones(num_features))
self.register_buffer('num_batches_tracked', torch.tensor(0, dtype=torch.long))
else:
self.register_parameter('running_mean', None)
self.register_parameter('running_var', None)
self.register_parameter('num_batches_tracked', None)
self.reset_parameters()
- 模型结构无参数层
网络中其实有很多op,仅仅是做一些维度变换、索引取值或者上/下采样的操作,例如:
Reshape
Squeeze
Unsqueeze
Split
Transpose
Gather
这些操作没有参数仅仅是对上一层传递过来的张量进行维度变换。有时候在通过Pytorch转换为ONNX的时候,偶尔会发生一些转换诡异的情况。比如一个简单的reshape会四分五裂为gather+slip+concat,这种操作相当于复杂化了,不过一般来说这种情况可以使用ONNX-SIMPLIFY去优化掉,当然遇到较为复杂的就需要自行优化了。此外,对于这些变形类的操作算子,其实有些是有参数的,例如下图的reshap
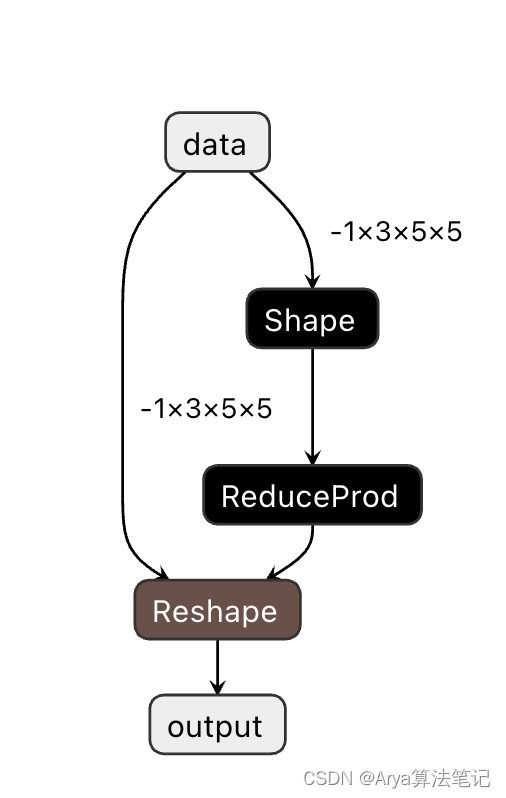
像这种的op,有时候会比较棘手。如果想要将这个ONNX模型转换为TensorRT,那么100%会遇到问题,因为TensorRT的解释器在解析ONNX的时候,不支持reshape层的shape是输入TensorRT,而是把这个shape当成attribute来处理,而ONNX的推理框架Inference则是支持的。
state_dict的value:
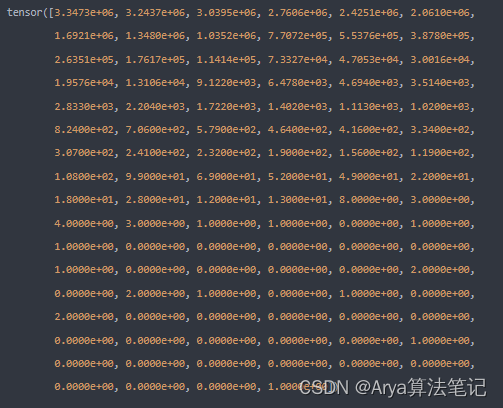
模型训练出的各层参数,都是有固定精度的0-1数据。通常来说,pth文件的参数精度为FP32,然而对于模型参数的部署来说我们需要在硬件中进行精度和推理速度之间的协调。
不过执行模型操作(卷积、全连接、反卷积)的算子会变化,可能从Pytorch->TensorRT或者TensorFlow->TFLITE,也就是实现算子的方式变了,同一个卷积操作,在Pytorch框架中是一种实现,在TensorRT又是另一种实践,两者的基本原理是一样的,但是精度和速度不一样,TensorRT可以借助Pytorch训练好的卷积的权重,实现与Pytorch中一样的操作,不过可能更快些。
参数精度
浮点数精度:双精度(FP64)、单精度(FP32、TF32)、半精度(FP16、BF16)、8位精度(FP8)、4位精度(FP4、NF4)
量化精度:INT8、INT4 (也有INT3/INT5/INT6的)
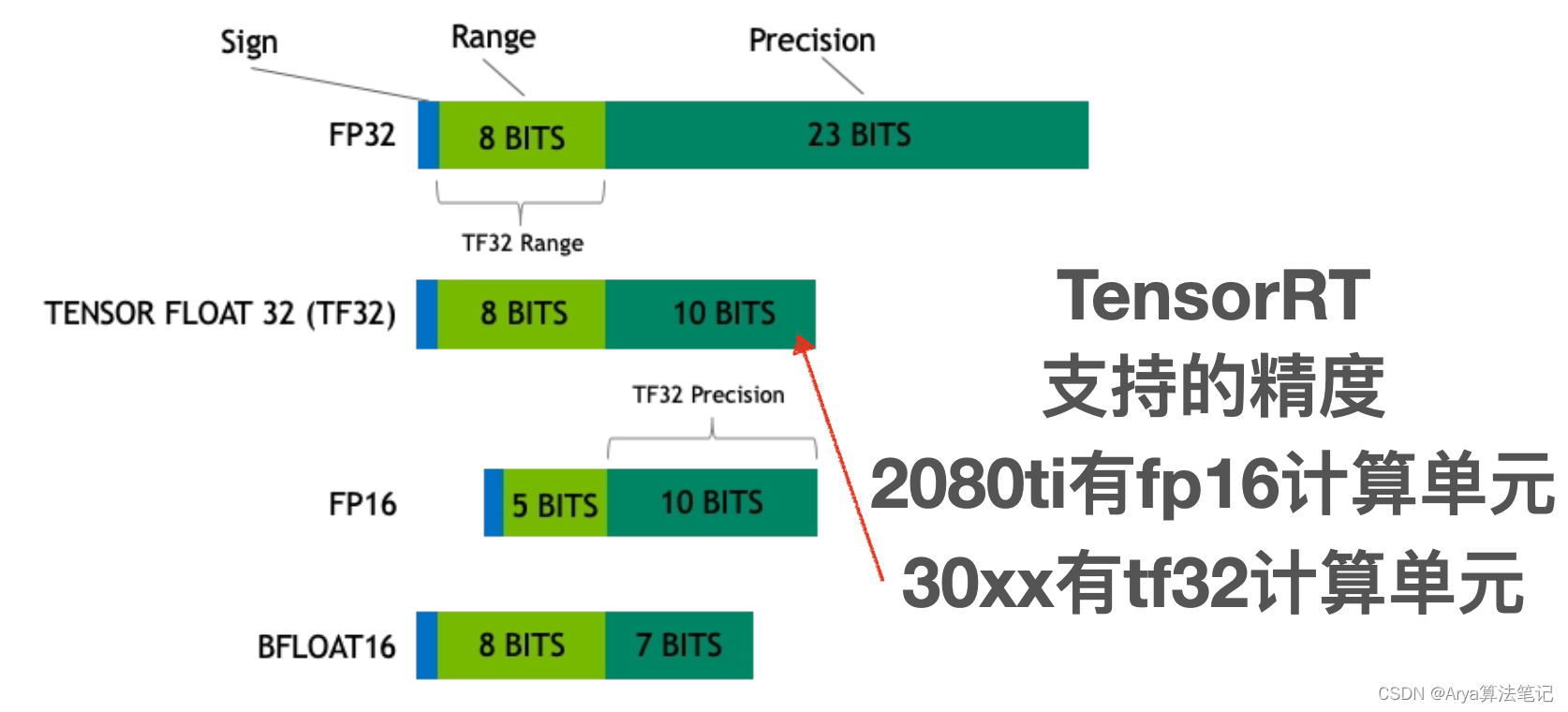
为什么要有这么多精度
因为成本和准确度。
都知道精度高肯定更准确,但是也会带来更高的计算和存储成本。**较低的精度会降低计算精度,但可以提高计算效率和性能。**所以多种不同精度,可以让你在不同情况下选择最适合的一种。
双精度比单精度表达的更精确,但是存储占用多一倍,计算耗时也更高,如果单精度足够,就没必要双精度。
但如何评估是否要进行精度降低?
不同的浮点数精度
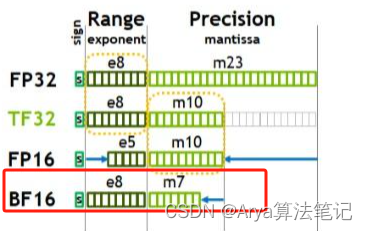
在计算机中,浮点数存储方式,由由**符号位(sign)、指数位(exponent)和小数位(fraction)**三部分组成。符号位都是1位,指数位影响浮点数范围,小数位影响精度。
FP精度
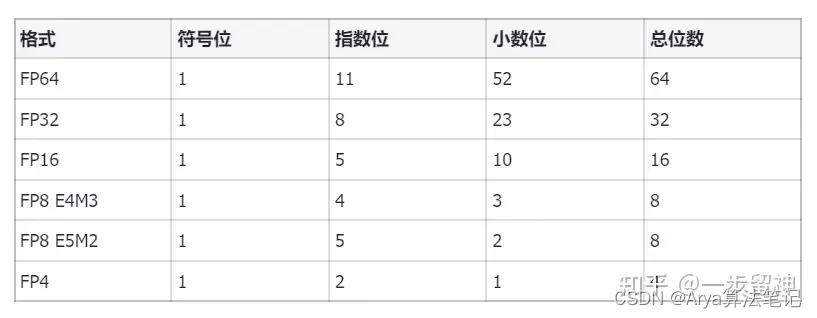
特殊精度
- TF32(1,8,10)
其实只有19位,Tensor Float 32,英伟达针对机器学习设计的一种特殊的数值类型,用于替代FP32。首次在A100 GPU中支持。

- BF16(1,8,7)
Brain Float 16,由Google Brain提出,也是为了机器学习而设计。由1个符号位,8位指数位(和FP32一致)和7位小数位(低于FP16)组成。所以精度低于FP16,但是表示范围和FP32一致,和FP32之间很容易转换。在 NVIDIA GPU 上,只有 Ampere 架构以及之后的GPU 才支持。
- NF4
4-bit NormalFloat,一种用于量化的特殊格式,于23年5月由华盛顿大学在QLoRA量化论文中提出,论文地址:https://arxiv.org/abs/2305.14314
NF4是建立在分位数量化技术的基础之上的一种信息理论上最优的数据类型。把4位的数字归一化到均值为 0,标准差为 [-1,1] 的正态分布的固定期望值上,知道量化原理的应该就会理解。
一般情况下,精度越低,模型尺寸和推理内存占用越少,为了尽可能的减少资源占用,量化算法被发明。FP32占用4个字节,量化为8位,只需要1个字节。常用的是INT8和INT4,也有其他量化格式(6位、5位甚至3位)。虽然资源占用减少,但是推理结果差不了多少。那么接下来就是我们说到的量化问题。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Mybatis源码总结
- 铝合金钻孔大功率大扭矩高速主轴
- RabbitMQ之MQ可靠性
- 深入解析JavaScript中的函数绑定和命名函数表达式
- 吴恩达chatgpt学习
- 年度技术回顾总结与拓展
- 【NodeJS】html通过video和canvas同时播放视频
- R语言【CoordinateCleaner】——cc_dupl():根据物种名称和坐标以及用户定义的附加列删除或标记重复的记录
- 315m无线模块怎么接收程序以及程序代码
- NWN、百利、希喂猫咪主食冻干哪款好?三款主食冻干真实对比测评