[力扣 Hot100]Day11 滑动窗口最大值
发布时间:2024年01月23日
题目描述
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
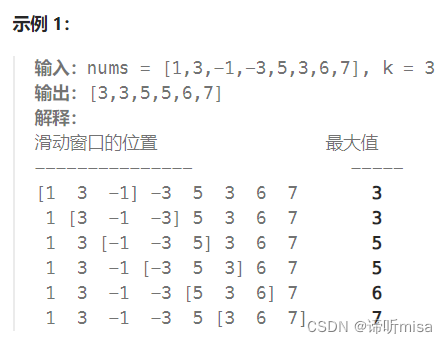
思路
暴力解法就是O(n*k)会超时,所以要用单调数列。维护一个单调递减的队列,队列初始元素是初始窗口内的值,随后移动窗口时维护这个单调队列。窗口滑动一次的操作分三步:
pop:如果窗口左pop掉的不是队列front,说明窗口左并不在队列中(最大值左边的所有数都不会加入队列),不用操作,如果窗口左pop掉的恰是队列front,pop掉队列的front。
push:如果窗口右push的比队列back还小,队列直接push_back,否则先pop掉队列内比待push值小的所有项再push_back,这样就可以保证队列单调。
get_result:每轮pop和push后(即窗口滑动一次的操作)队列必定非空(极端情况下队列全pop完了只push了一个最大值),此时队头即为窗口最大值。
代码
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
int n = nums.size();
deque<int> q;
vector<int> result;
//构建初始单调序列
for(int i = 0; i < k; i++){
while(!q.empty()&&nums[i]>q.back())
q.pop_back();
q.push_back(nums[i]);
}
result.push_back(q.front());
for(int i = k; i < n; i++){
if(!q.empty()&&nums[i-k]==q.front())//要删的是最大值
q.pop_front();
while(!q.empty()&&nums[i]>q.back())
q.pop_back();
q.push_back(nums[i]);
result.push_back(q.front());
}
return result;
}
};
文章来源:https://blog.csdn.net/qq_53627591/article/details/135763480
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 系统架构14 - 软件工程(2)
- Windows 安装RocketMQ
- 详解git如何回滚提交记录
- 1 快速前端开发
- JAVAEE初阶 文件IO(一)
- 聊聊PowerJob的StoreStrategy
- Jenkins Tutorial
- 开发可复用的WebService接口并将其封装成Java库(jar包),如何做技术选型?
- 【硕士论文复现】可再生能源发电与电动汽车的协同调度策略研究(Matlab代码实现)
- uni-app顶部导航条固定