SLAM中三角测量求解特征点世界坐标系下坐标Pw的方法

一.SVD分解法

1.SVD分解的介绍

???

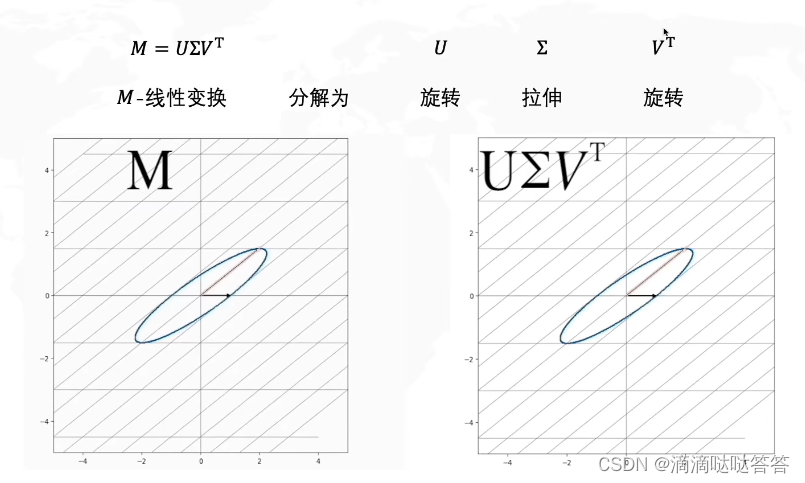
SVD分解的本质就是将一个线性变换 M 分解为旋转 左乘拉伸 再左乘旋转U。

??? U和V都表示旋转，均为单位正交矩阵，即满足

，

，

??? 有时也称作酉矩阵（Unitary Matrix）（矩阵的共轭转置（也称为厄米共轭或伴随矩阵）等于其逆矩阵。

??? ? ? 的性质如下图中所示：

???

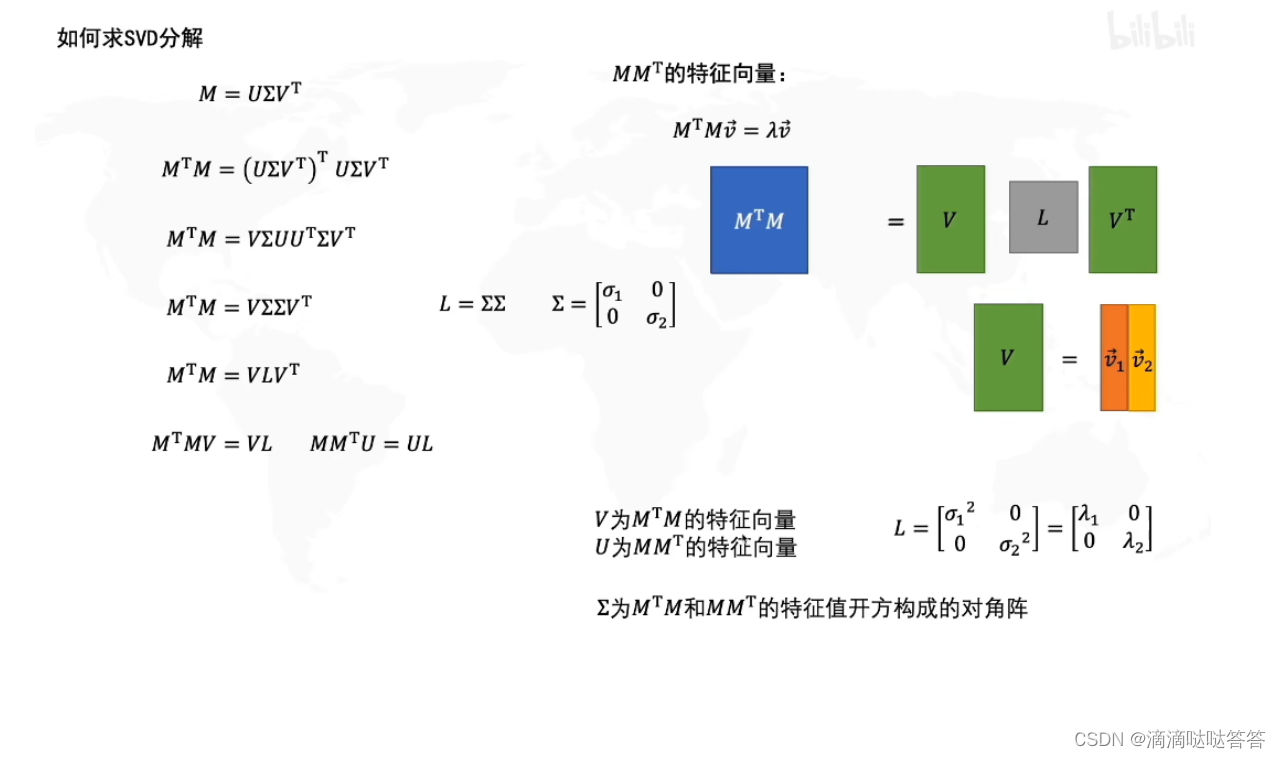
求矩阵M的SVD分解的步骤如下：

?2.SVD分解法的推导

?注意：

???????? 这里的pr1和pr2表示的含义如下，此时，对应的u和v为特征点在像素坐标系下的坐标

??????? 当pr1和pr2表示的含义如下时（即不包括相机内参时），对应的u和v变为特征点在归一化坐标系下的坐标?

3.SVD分解法的求解

??? 先给出结论：Ax=0的最小二乘解是最小特征值对应的特征向量

??? 取SVD分解得到的V矩阵最后一列作为 P 1的解，但我们还需要归一化以后才能使用。
??? 对于超定方程Ax=0，没有真正的非零解析解，因为约束太多，没法都满足(零向量除外)，求其最小二乘解近似。

理论推导部分
齐次方程组形如： A x = 0 。
在一些优化，拟合等问题中经常出现，我们常考虑方程多于未知数元数的情况------超定方程组。

首先对于平凡解x=0我们一般不感兴趣，一般我们会寻求方程组的非零解。

如果x是方程组的一个解，那么对于 V k ∈ R , kx也是齐次方程组的解，一个合理的假设是只求满足? 的解。

假设A的维数是 m × n ，一般的 m > n (超定)，没有真正的非零解析解。当没有精确解的时候，我们通常求其最小二乘解，描述为：

求使||Ax||最小化并满足||x||=1的 x

先介绍一个引理，即对于一个酉阵 p（）和一个向量x(向量维数等于P列数)，有：

?

至此，求解完毕。

参考：

????? 【学长小课堂】什么是奇异值分解SVD--SVD如何分解时空矩阵

????????奇异值分解（Singular Values Decomposition，SVD）

????????SLAM--三角测量SVD分解法、最小二乘法及R t矩阵的判断

????????奇异值分解（SVD）方法求解最小二乘问题

????????????????