后缀自动机超详细

后缀自动机

1.关于$endpos$

理解含义

假设字符串s是字符串S的一个子串，则$endpos(s)$表示s在S中的所有结束位置，如在字符串$abcabcab$中，$endpos(ab)=2，5，8$。

如果$endpos(s_1)=endpos(s_2)$，则称s与s在同一等价类中。因此可以根据$endpos(s)$的值将字符串S的所有子串进行划分。

理解定理

引理 1： 字符串S的两个非空子串$s1$和$s2$的$endpos$相同（并且$s1$的长度小于等于$s2$的长度），当且仅当字符串$s1$在S中的每次出现，都是以$s2$后缀的形式存在的。

证明：这个我们要根据$endpos$的定义来，以$abcabcabc$举例，$endpos(abc)=endpos(bc)=3,6,9$。这里$bc=s_1，abc=s_2$，$bc$每次在字符串中出现都是以$abc$的后缀的形式。

引理 2： 考虑两个非空子串$s1$和$s2$的$endpos$相同（并且$s1$的长度小于等于$s2$的长度）。那么要么$endpos(s_1)\cap endpos(s_2)=?$，要么$endpos(s_2)?endpos(s_1)$，取决于$s1$是否为$s2$的一个后缀。

如果$s1$是$s2$的一个后缀，则$endpos(s_2)?endpos(s_1)$，否则$endpos(s_1)\cap endpos(s_2)=?$。

证明：如果$s1$是$s2$的一个后缀，则$s2$出现的地方，$s1$一定出现，反之不然，所以$s2$出现的地方一定被包含在$s1$出现的地方里。如果$s1$不是$s2$的一个后缀，那么$s2$出现的地方一定不是$s1$出现的地方。那你会问，如果$s2$里面包含了$s1$呢？比如$abcabcabc$中，$abc$和$b$，但是$endpos(abc)=3,6,9$，而$endpos(b)=2,5,8$，你看，两者必然不一样。为什么我们关心的是后缀？因为$endpos$记录的是字符串的结束位置。

引理 3： 考虑字符串的$endpos$等价类，对于同一等价类的任一两子串，较短者为较长者的后缀，设最长的字符串为y，最短的字符串为x，则该等价类中的子串长度恰好覆盖整个区间$[len(x),len(y)]$。

证明：直接用例子吧，$abcdabcdabcd$里的$endpos=4,8,12$的子串有$abcd，bcd，cd，d$，最长的子串为$abcd$，最短的子串为$d$，可以看见除了最短的子串$d$，其余子串皆是最长子串的后缀，那么这些子串直接的长度一定是连续的4->3->2->1。那么其实这个等价类涵盖了$abcd$的所有后缀子串，但是一定会这样吗？一个字符串的后缀子串一定和它在同一个等价类里？再换一个例子$abcdabcdabcdd$里的$endpos=4,8,12$的子串有$abcd，bcd，cd$，可以看到此时$d$就不在这个等价类里，因为它在原串里不仅仅以$abcd$的后缀出现，也以其它方式出现，所以它的$endpos$应该比$abcd$多，也就是引理2。$endpos(d)=4,8,12,13$。

2.后缀自动机里的$endpos$树

接下来，我要证明根据$endpos$划分的等价类可以形成一颗树。一个节点的父节点是谁呢？回顾一下刚刚举的例子，$endpos(abcd)?endpos(d)$，那么其实$abcd$是$d$的儿子节点，因为它的出现位置包含在$d$中，那么同样的$endpos(abcd)$的其它等价类也是，我们把在同一等价类中的子串放在一个节点里，那么节点2包含子串$abcd，bcd，cd$，它的父节点是节点1，节点1包含子串$d$。

现在给一个字符串$aababa$，按照$endpos$划分的等价类构成一颗树，如下图所示，可以先自己试着画一画哦。

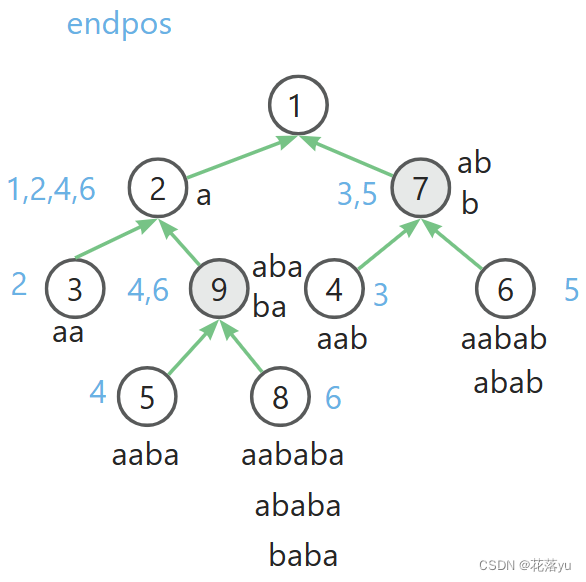
可以看见，其实$endpos$的作用就是对字符串的子串进行压缩，比如8号节点，我通过1个节点存了3个节点的信息。那么除了树必须要记录的父节点信息，我还需要记录什么信息呢？还需要记录每个节点的最长串的长度，那么最为什么不用记录最短串的长度呢？因为我们可以直接用最长串的长度表示。

fa[x]：存节点x的父节点

len[x]：存节点x的最长串的长度

节点x最短串的长度=$len[x]?len[fa[x]]+1$，如$len[8]=6,fa[8]=9,len[9]=3,len[8]?len[9]+1=6?3+1=4$，刚好是节点8的最短串的长度

节点的子串数量=$len[x]?len[fa[x]]$，如$len[6]?len[7]=3，len[7]?len[1]=2$

我们是不是还差一点信息呢？一个子串可能不仅仅在原串中出现一次，是的，我们还需要记录每个子串的出现次数。在这之前，我们需要达成一个共识，就是属于同一个等价类的节点出现次数是相同的。这个其实也是显而易见的，因为他们的出现位置相同必然出现次数也相同。

我们还需要再达成一个共识，这个比较重要，我们另起一段，那就是一个节点的出现次数是它单独出现的次数+它作为后缀在其它字符串里出现的次数。什么时候它会单独出现而不是作为其它字符的后缀出现？先自己想哈，它不是其它子串的后缀，那么它必然是以原字符串前缀的形式出现。如$abcabcabc$，这里面a本身自己出现的次数是1，作为后缀在其它字符串里出现的次数是2，$abca$本身自己出现的次数是1。

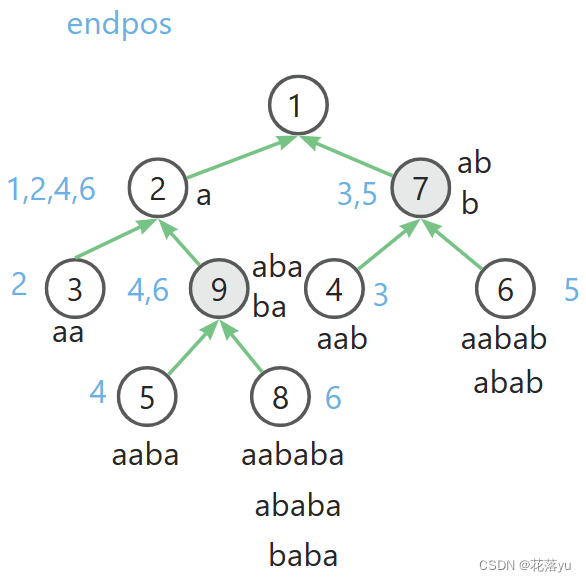
再来看这棵树，节点对于字符串$aababa$，我们用数组$cnt$存储遍历字符串的过程中字符串的前缀子串出现的次数，其实也就是1。那么我们来看，$cnt[2]=1,cnt[6]=1,cnt[9]=0$，为什么$cnt[9]=0$？你可以看见节点9是$aba$和$ba$，他们都不是$aababa$的前缀，而节点2的字符串是$aa$，节点6的字符串$aabab$都是前缀。但是你还会问，那节点6里面还存了$abab$，他不是前缀呀？因为i前缀$aabab$里面已经包含了$abab$了呀。而$aabab$又不是$abab$的父节点，如果不在这里给他记录，那么这一次的出现就丢失了，或者另一种解释，同一个等价类里的子串出现次数是相同的，所以我可以用一个$cnt[i]$数组表示该节点里所有子串的出现次数。现在$cnt$的值只是初始建树的过程中赋予的，那么后面我们再求才能知道到底出现了几次，怎么求？累加上子节点的出现次数！因为子节点的字符串是包含当前节点的字符串的。

$cnt[2]=cnt[2]+cnt[3]+cnt[9]=cnt[2]+cnt[3]+cnt[5]+cnt[8]=1+1+2=1+1+1+1=4$

可以用递归去求，代码如下，代码里的size和$cnt$数组的含义一样

		private void dfs(int u) {
			// TODO Auto-generated method stub
//			sam.get(u).size = 1;
			if(tree.get(u) != null) {
				for(int e:tree.get(u)) {
					dfs(e);
					sam.get(u).size += sam.get(e).size;
				}
			}
		}

分析到这里，这颗树还差最后一个点了，那就是图里的灰色节点是什么情况呢？这里我们就要真正讨论后缀自动机的构建了，关键是构建这棵树，这棵树上的边在后缀自动机里称为链接边。

后缀自动机存两类边，链接边和转移边。链接边就是来建树的，沿着转移边走可以形成一个子串。

3.后缀自动机代码

话痨版证明

我们来模拟一下自动机形成的过程吧。

private void extend(int x) {//要往后缀自动机里插入的字符
			// TODO Auto-generated method stub
			sam.add(new node());
			sam.add(new node());//java的原因，因为下标从1开始，所以预存两个节点分别表示节点0和节点1
			int p = las;//记录上一个节点
			int np = ++tot;//np表示要插入节点的编号
			las = np;
			sam.add(new node());//新建一个节点
			sam.get(np).len = sam.get(p).len+1;
			//p沿链接边回跳，从旧点向新点建转移边 ch[p][x]
			for(;p!=0&&sam.get(p).map.get(x)==null;p=sam.get(p).par) sam.get(p).map.put(x, np);
			if(p==0) {//插入的点是一个新点，回跳边直接连到根节点上
				sam.get(np).par=rt;
			}else {
				int q = sam.get(p).map.get(x);//p沿x可以到达的点
				if(sam.get(q).len == sam.get(p).len+1) {//弱q和p相邻
					sam.get(np).par = q;//是合法点，回跳边连接到q上
				}else {
					int nq = ++tot;//不是合法点，要裂点新建
					sam.add(new node());
					sam.get(nq).len = sam.get(p).len+1;//新点的长度等于旧点的长度
//					HashMap<Integer, Integer> tempmap = new HashMap<Integer, Integer>();
//					tempmap.putAll(tempmap);
					sam.get(nq).map.putAll(sam.get(q).map);//这里要深拷贝,把旧点指出去的边复制给新节点
//					sam.get(nq).map = sam.get(q).map;//新点连出去的边等于旧点连出去的边
					sam.get(nq).par = sam.get(q).par;//新点的回跳边等于旧点的回跳边
					sam.get(q).par = nq;//旧点的回跳边等于新点
					sam.get(np).par = nq;//插入点的回跳边等于新点
					for (;p!=0&& sam.get(p).map.get(x) == q; p = sam.get(p).par) 
						sam.get(p).map.put(x, nq);}//连到旧点的边指向新点
			}

1. 初始时，只有一个节点1（用p表示旧节点，也就是存前一个字符的节点），这时我插入一个字符a，那么用节点2（用$np$表示新节点）表示该字符的状态，节点2自然要连到节点1的后面，并且节点2记录的字符串的长度要比节点1记录的字符串长度大1（sam.get(np).len = sam.get(p).len+1;），因为在节点1的基础上多了节点2所代表的这个字符嘛。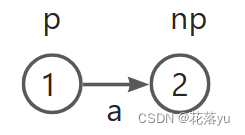

   

2. 当新插入一个节点时，我要建转移边。建转移边的代码为for(;p!=0&&sam.get(p).map.get(x)==null;p=sam.get(p).par) sam.get(p).map.put(x, np);我有两个问题，

   问题1：转移边的作用是什么？

   问题2：为什么是沿着转移边回跳？

? 最好是自己先想哈！我们在讲树的时候，每个节点表示了多个子串，其实后缀自动机里的节点和$endpos$树里的节点是同一个，那么想一想字典树，从根节点沿着边走，走过的所有边表示的字符串起来形成一个字符串，这里也是同理。

如图，这里的节点6表示了哪些字符串呢？$aababa,bab,abab$，就是从节点1开始沿着转移边走走到节点6形成的字符串，那么它们其实也是以节点字符b结尾的子串。这里的思想有点类似AC自动机了。其实我要求以字符b结尾的子串，首先字符b节点（节点6）的前一个节点（节点5），它一定有条转移边指向b。然后我需要找到节点5的所有后缀，让他们也有一个转移边指向b。那么其实就是不断沿着节点的链接边回跳。因为链接边的两端是父节点和子节点的关系，同时节点的链接边指向的就是该节点的后缀，这是我们在讲树的时候讲到的。回跳到什么情况我就停止呢？想一想，停止是因为我把以b结尾的子串都知道了，如果我们的字符b是第一次出现，那么必然要一直跳到节点1，如果字符b之前出现过呢？我只需要跳到他出现过的地方就可以停了。

? 好，回到我们刚刚的构建过程，下面我们要插入字符a，节点2向节点3连转移边，然后把p指向节点2的链接边指向的节点1，此时p指向节点1，但是节点1已经有沿a走的转移边了，那我们就不需要给它建变了，我们的转移边停止建边，退出while循环，同时也说明字符a之前出现过。节点3的链接边连向节点1沿a指向的节点，也就是节点2。我们在抽象版里解释这里为什么可以停止建转移边。

下面我们要插入字符b，节点3向节点4连转移边，然后把p指向节点3的链接边指向的节点2，此时p指向节点2，节点2没有沿b走的转移边了，那么我们就给他建沿b走的转移边且指向节点4；然后把p指向节点2的链接边指向的节点1，此时p指向节点1，节点1没有沿b走的转移边了，那么我们就给他建沿b走的转移边且指向节点4，节点1的链接边指向节点0，此时退出while循环，也说明了b字符之前没有出现过，那么节点4的链接边指向节点1。之前没有出现过，那也就不存在后缀，所以指向节点1没有问题。

下面我们要插入字符a，节点4向节点5连转移边，然后把p指向节点4的链接边指向的节点1，此时p指向节点1，节点1有沿a走的转移边了，停止建转移边，并且节点5的链接边指向节点1有沿a走的转移边指向的节点，即节点2。

下面我们要插入字符b，节点5向节点6连转移边，然后把p指向节点5的链接边指向的节点2，此时p指向节点2，节点2有沿b走的转移边了，停止建转移边，并且节点6的链接边指向节点2有沿b走的转移边指向的节点，即节点4，也就是红色的线段。我们来看一下这样建边有什么不妥之处。节点6表示的字符串有$aabab,abab,bab$，节点4表示的字符串有$aab,ab,b$，在加入字符b之前，$aab,ab,b$的出现位置都是3，但是加入了字符b后，$b$和$ab$的出现位置就变成了3，5。所以此时$b,ab$和$aab$分开。那我们要新建一个节点7，这个节点7要存什么呢？这个节点7的边的关系又如何去表示呢？节点7存的是$b,ab$，为啥？

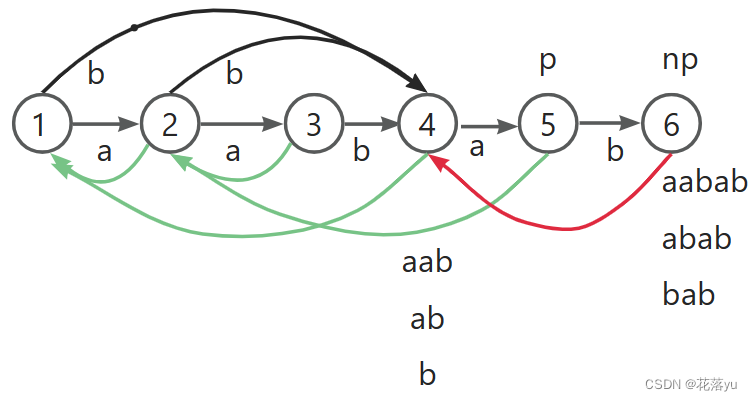
之前分析的时候，正常的点应该存了字符串的前缀，而这里$aab$是字符串的前缀，应该让他留在节点4里面。接下来看裂点后链接边怎么修改，链接边指向的是当前节点的后缀，那么此时节点4应该指向节点7，因为他们的后缀是$ab$和$b$，那么节点4链接边原本指向的节点由节点7去指。不要忘了裂点的目的，让节点6链接边指向节点7。转移边又该如何去变呢？原本从节点4指出去的转移边也要从节点7指出去，原本沿b指向节点4的转移边现在改成指向节点7。

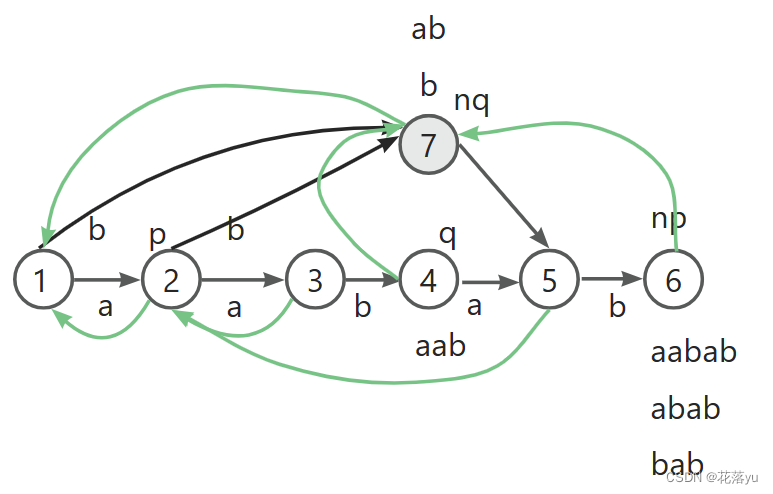
实例就讲到这里，还差最后一个字符，大家可以自己试试怎么插，那么完整的后缀自动机如下图，

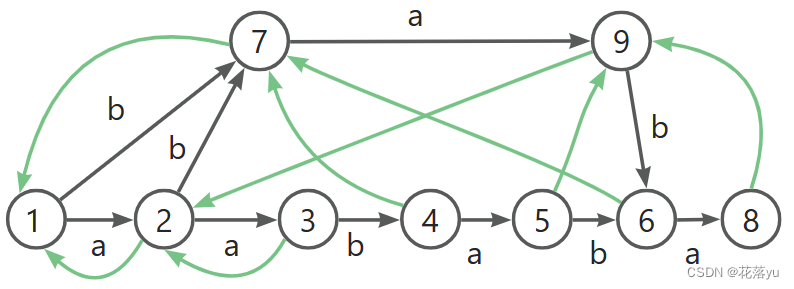
抽象版证明

private void extend(int x) {
			// TODO Auto-generated method stub
			sam.add(new node());
			sam.add(new node());
			int p = las;//记录上一个节点
			int np = ++tot;//np表示要插入节点的编号
			las = np;
			sam.add(new node());
			sam.get(np).len = sam.get(p).len+1;
			//p沿链接边回跳，从旧点向新点建转移边 ch[p][x]
			for(;p!=0&&sam.get(p).map.get(x)==null;p=sam.get(p).par) sam.get(p).map.put(x, np);
			if(p==0) {//插入的点是一个新点，回跳边直接连到根节点上
				sam.get(np).par=rt;
			}else {
				int q = sam.get(p).map.get(x);//p沿x可以到达的点
				if(sam.get(q).len == sam.get(p).len+1) {//弱q和p相邻
					sam.get(np).par = q;//是合法点，回跳边连接到q上
				}else {
					int nq = ++tot;//不是合法点，要裂点新建
					sam.add(new node());
					sam.get(nq).len = sam.get(p).len+1;//新点的长度等于旧点的长度
//					HashMap<Integer, Integer> tempmap = new HashMap<Integer, Integer>();
//					tempmap.putAll(tempmap);
					sam.get(nq).map.putAll(sam.get(q).map);//这里要深拷贝,把旧点指出去的边复制给新节点
//					sam.get(nq).map = sam.get(q).map;//新点连出去的边等于旧点连出去的边
					sam.get(nq).par = sam.get(q).par;//新点的回跳边等于旧点的回跳边
					sam.get(q).par = nq;//旧点的回跳边等于新点
					sam.get(np).par = nq;//插入点的回跳边等于新点
					for (;p!=0&& sam.get(p).map.get(x) == q; p = sam.get(p).par) 
						sam.get(p).map.put(x, nq);}//连到旧点的边指向新点
			}
		}

sam.get(np).len = sam.get(p).len+1;假设新插入的节点是c，新插入节点所表示字符串的长度是前一个节点的长度+1，因为比前一个节点多了一个字符c。

for(;p!=0&&sam.get(p).map.get(x)==null;p=sam.get(p).par) sam.get(p).map.put(x, np);这个代码的含义其实就是在前一个节点的所有后缀上加一个字符c，当然，如果本来就有字符c，也就是本来就有沿c走的转移边我就不加了。如前一个字符串是$abad$，我要加一个新字符c，那么实际会产生的新字符串应该是$abad+c,bad+c,ad+c,d+c$，也就是在$abad$的所有后缀里面添加一个字符c。如果没有走到底是什么情况呢？比如$aaba$里面添加一个字符b，产生的新字符串是$aaba+b,aba+b,ba+b,a+b$，但是实际产生的新字符串应该是$aaba+b,aba+b,ba+b$，ab在插入b之前就已经存在了，那么在建转移边的过程中，因为表示字符串a的节点此时已经有沿b的转移边了，所以为了不重复，就不再往下走了，当然当前这个节点也不再建边。

if(p==0)如果p=0，说明当前字符是新插入的字符，自然没有后缀，直接连在根节点上。

if(p==0) {//插入的点是一个新点，回跳边直接连到根节点上
				sam.get(np).par=rt;
			}

如果p停在了半路，说明字符是旧字符，如果p沿字符x走到的节点与p长度相差1，则链接边直接连到q。链接边指向后缀，该后缀的出现位置比当前字符串多。p沿字符x走到的节点所代表的字符串一定是当前字符串的后缀，且它在当前字符串出现之前就已经存在了，必然其出现位置比当前字符串多，且包含当前字符串出现的位置。

int q = sam.get(p).map.get(x);//p沿x可以到达的点
if(sam.get(q).len == sam.get(p).len+1) {//弱q和p相邻
		sam.get(np).par = q;//是合法点，回跳边连接到q上
}

但是为什么要判断sam.get(q).len == sam.get(p).len+1呢？我们之前在建树时提到节点内子串的长度是连续的，父子节点之间也是连续的，如果出现了不连续的情况，说明当前节点记录的子串因为后续字符的加入而不再属于同一等价类，也就是不合法。为什么不合法，因为受插入字符串的影响，某些字符串的出现次数增多。我把出现次数增多的字符串分出来，新建一个节点存它，新节点的长度此时一定是合法的，据此更新一下它的长度

int nq = ++tot;//不是合法点，要裂点新建
sam.add(new node());
sam.get(nq).len = sam.get(p).len+1;//新点的长度等于旧点的长度

出现次数多的子串一定是出现次数少的子串的后缀，所以原节点和新插入节点的链接边都指向它，原节点的链接边给它，

sam.get(nq).par = sam.get(q).par;//新点的回跳边等于旧点的回跳边
sam.get(q).par = nq;//旧点的回跳边等于新点
sam.get(np).par = nq;//插入点的回跳边等于新点

原本从旧点连出去的转移边也要从新点转移出去

sam.get(nq).map.putAll(sam.get(q).map);//这里要深拷贝,把旧点指出去的边复制给新节点

在一开始我们满足sam.get(p).map.get(x)！=null就暂停了，因为再向后遍历必然也存在沿x走的转移边，得到的后缀串也是已经出现过的，也说明从这里向后的字符串的出现位置比原来多，所以他们应该被放在新建的节点中，所以原本连向旧点的转移边改成连向新点。

for (;p!=0&& sam.get(p).map.get(x) == q; p = sam.get(p).par) 
	sam.get(p).map.put(x, nq);//连到旧点的边指向新点

至此后缀自动机的模板代码就解读完毕了，不仅仅要知道应该这样写，也要知道为什么这样写，最顶端的思考应该是知道如何想到的这样写，但是我不会，就不写了。

4.后缀自动机完整代码

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;

public class ok后缀自动机2 {
	static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
	static String[] string; 
	static class SAM{
		class node{
			int par,len;
			Map<Integer, Integer> map = new HashMap<Integer, Integer>();
		}
		List<node> sam = new ArrayList<node>();
		int las,rt,tot;		
		SAM(int n) throws IOException{
			las = 1;rt = 1;tot = 1;
			long ans = 0;
			string = br.readLine().split(" ");
			for(int i = 0;i < n;i++) {
				int x = Integer.parseInt(string[i]);
				extend(x);
				ans += sam.get(las).len - sam.get(sam.get(las).par).len;//回顾后缀自动机的规律
				System.out.println(ans + " " +(sam.get(las).len - sam.get(sam.get(las).par).len)+" "+las+" "+sam.get(las).par);
			}
            System.out.println(4+" "+sam.get(4).par);			
		}
		private void extend(int x) {
			sam.add(new node());
			sam.add(new node());
			int p = las;//记录上一个节点
			int np = ++tot;//np表示要插入节点的编号
			las = np;
			sam.add(new node());
			sam.get(np).len = sam.get(p).len+1;
			//p沿链接边回跳，从旧点向新点建转移边 ch[p][x]
			for(;p!=0&&sam.get(p).map.get(x)==null;p=sam.get(p).par) sam.get(p).map.put(x, np);
			if(p==0) {//插入的点是一个新点，回跳边直接连到根节点上
				sam.get(np).par=rt;
			}else {
				int q = sam.get(p).map.get(x);//p沿x可以到达的点
				if(sam.get(q).len == sam.get(p).len+1) {//弱q和p相邻
					sam.get(np).par = q;//是合法点，回跳边连接到q上
				}else {
					int nq = ++tot;//不是合法点，要裂点新建
					sam.add(new node());
					sam.get(nq).len = sam.get(p).len+1;//新点的长度等于旧点的长度
					sam.get(nq).map.putAll(sam.get(q).map);//这里要深拷贝,把旧点指出去的边复制给新节点
					sam.get(nq).par = sam.get(q).par;//新点的回跳边等于旧点的回跳边
					sam.get(q).par = nq;//旧点的回跳边等于新点
					sam.get(np).par = nq;//插入点的回跳边等于新点
					for (;p!=0&& sam.get(p).map.get(x) == q; p = sam.get(p).par) 
						sam.get(p).map.put(x, nq);}//连到旧点的边指向新点
			}
		}
	}
public static void main(String[] args) throws IOException {
	solve();
}
private static void solve() throws IOException {
	// TODO Auto-generated method stub
	string = br.readLine().split(" ");
	int n = Integer.parseInt(string[0]);
	SAM A = new SAM(n);
}
}

SAM构造函数是根据题目来的，可以不做思考，关键关注extend函数。