梯度消失与梯度爆炸的问题小结

本文参考李沐老师动手深度学习,上篇激活函数有遇到这个问题我们来深入探讨一下

前言

一、梯度爆炸

二、梯度爆炸的问题

三、梯度消失

四.梯度消失的问题

总结

---

前言

? ? ? ? 到目前为止，我们实现的每个模型都是根据某个预先指定的分布来初始化模型的参数。 有人会认为初始化方案是理所当然的，忽略了如何做出这些选择的细节。甚至有人可能会觉得，初始化方案的选择并不是特别重要。 相反，初始化方案的选择在神经网络学习中起着举足轻重的作用， 它对保持数值稳定性至关重要。 此外，这些初始化方案的选择可以与非线性激活函数的选择有趣的结合在一起。 我们选择哪个函数以及如何初始化参数可以决定优化算法收敛的速度有多快。 糟糕选择可能会导致我们在训练时遇到梯度爆炸或梯度消失。

---

4.8. 数值稳定性和模型初始化 — 动手学深度学习 2.0.0 documentation (d2l.ai)

一、梯度爆炸

首先我们就需要回顾一下反向传播求导的计算.也就是我们的链式法则,以及对梯度下降法的原理大致了解.

这个d-t很大也就是我们的深度很大这样累乘起来就会得到一个很大很大的值.

二、梯度爆炸的问题

三、梯度消失

最典型的例子就是我们的sigmoid函数,这个函数我们在激活函数中简单了解了一下什么叫梯度消失.

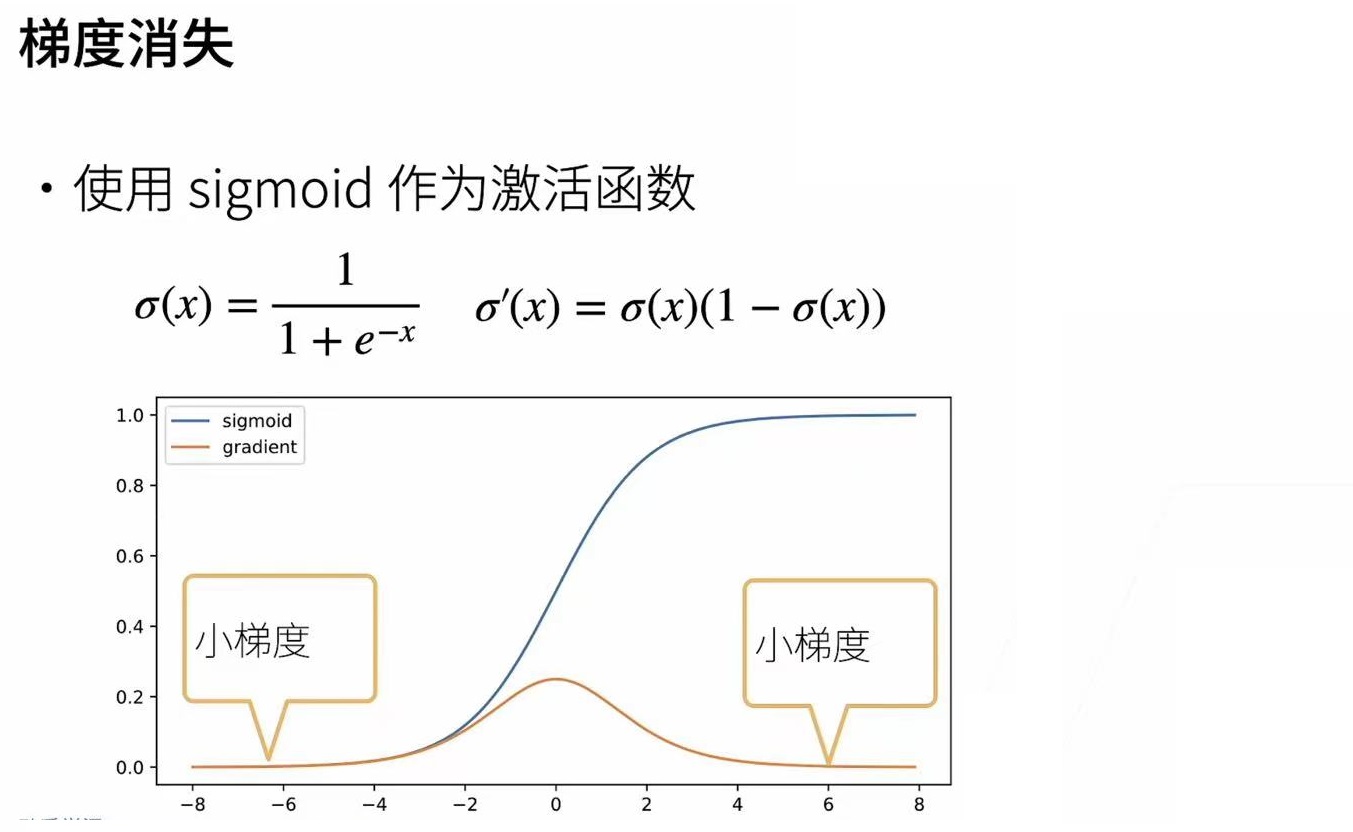
蓝色线为sigmoid函数图像,黄色是sigmoid梯度.

可见当梯度很小时,深度越深,这样累乘起来就会得到很小的数.导致梯度变化很小.

四.梯度消失的问题

梯度反向传播时对于底部,通过链式法则的累乘,梯度变化很小,所以跟那些深度很小的神经网络差不多.

---

总结

当数值过大或过小时会导致数值问题.

常常发生在深度模型当中,因为会对n个累乘.