二叉树(接口函数的实现)

今天继续来分享的是二叉树,我们废话不多说,直接来看下面的几个接口函数,然后我们把他们实现,我们就掌握二叉树的二分之一(今天粉丝破千了,属实有点高兴了)。
typedef char BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
// 二叉树销毁
void BinaryTreeDestory(BTNode* root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root);我们来看看第一个接口函数是创建,上来就是有点难度的接口,如果要实现这个数的样子的字符是"ABD##E#H##CF##G##"??那我们要创建出这样的一棵树,先要知道用前序遍历还是中序遍历这些,其实三种遍历方式都是可以实现的,这里用前序遍历比较好理解,我们写这个接口函数的时候,得自己创造节点,所以有一个CreateNode的函数得写好,其次就是我们来观察这个函数是有返回值的,按照前序遍历的方法就是根节点? 左孩子? 右孩子这样的写法,因此我们的代码就是下面的这个。
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
if (a[*pi] == '#')
{
(*pi)++;
return NULL;
}
BTNode* root = CreateNode(a[(*pi)++]);
root->left = BinaryTreeCreate(a, n, pi);
root->right = BinaryTreeCreate(a, n, pi);
return root;
}这里需要注意的一点就是pi是传递的是地址,pi需要我们进行解引用才可以的,我们的pi代表的意思就是数组的下标,然后我们来考虑为什么传的是指针,首先就是我们函数栈帧的开辟,局部变量都是随着函数栈帧的销毁而销毁的,其次还是那据最重要的话,形参是实参的一份临时拷贝。每次如果改变i的话只是在这个函数栈帧中起到作用。
void BinaryTreeDestory(BTNode* root)我们回创建节点,那肯定要会销毁节点,我们销毁节点就可以用后序遍历的思路,其实很简单,遇到空就可以返回,我们就直接给代码,但是我们这个代码会有点问题,但是可以加点代码来解决。
void BinaryTreeDestory(BTNode* root)
{
if (root == NULL)
{
return;
}
BinaryTreeDestory(root->left);
BinaryTreeDestory(root->right);
free(root);
root = NULL;
}
这里的问题就是还是形参是实参的一份临时拷贝,但是我们的root还能释放的原因是root虽然是形参,但是还是指向这片空间的,所以我们需要注意的就是在这个函数调用结束的时候加上这句就行了。

当然我们也可以传二级解决,但是我觉得没啥必要。
int BinaryTreeSize(BTNode* root)下一个接口函数就是我们来统计这颗树有多少个节点,到NULL就是开始返回,这里的子问题就是我们如何来统计我们左子树和右子树节点的个数,如果不为空就是有节点,我们只要返回节点个数,因为子问题就是左子树和右子树的个数,所以我们这里就可以写出下面的代码.
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}下一个接口函数是来统计我们的叶子节点的个数,叶子节点的统计我们分成子问题就是统计节点这个节点的左右孩子是空,那这个就是叶子节点,然后我们进行左子树和右子树的递归,再相加就可以解决问题了。
代码如下。
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}接下来的一个接口函数来实现的就是我们的统计K层的节点个数。
int BinaryTreeLevelKSize(BTNode* root, int k)这个首先我们得知道我们的树是怎么个样子的,下面这个图就是简易版这个题目的树,我们要来统计k层的节点个数。
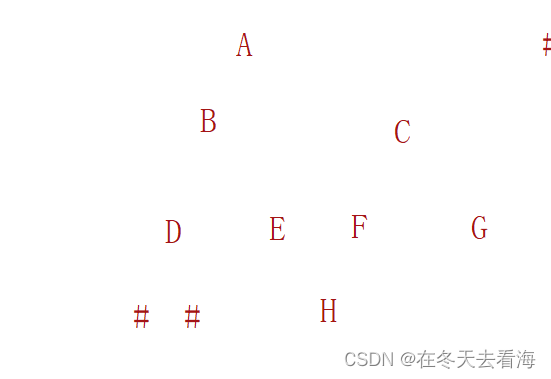
首先就是我们把他分成子问题就是我们只要到K层才开始统计,遇到空就返回,其实这样我们的代码也就是可以直接写出来,我们递归左子树和右子树然后进行相加就可以完成我们的代码了。
int BinaryTreeLevelKSize(BTNode* root, int k)
{
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
k--;
return BinaryTreeLevelKSize(root->left, k) +
BinaryTreeLevelKSize(root->right, k);
}
?这个需要我们注意就是只有当 k == 1的时候才是我们要来统计的时候,那我们就得让k--,并且能够递归到下一层,这样我们的代码也就能完成了。
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
这个就是找我们内容是x的节点,但是我们返回的时候是返回这个节点,返回的时候可能会出现问题,我们可以这样想这个题目,我们如果没找到就是返回空指针,如果找到了返回这个节点,但是我们要去左右子树递归找,我们不知道什么时候是找到以及他返回的是什么,我们可以保存下这个节点,这样我们再次判断就可以知道哪个是我们需要的。
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->data == x)
{
return root;
}
BTNode* ret1 = BinaryTreeFind(root->left, x);
BTNode* ret2 = BinaryTreeFind(root->right, x);
if (ret1)
{
return ret1;
}
if (ret2)
{
return ret2;
}
return NULL;
}后面的三个接口函数就相比起来要简单很多,我们可以来看看,这里呢我只写一个,另外两个真的太简单了,我就不写了。
oid BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);我们要来实现前序 中序和后序遍历,我们直接上手,遇到空就返回并打印其内容。
void BinaryTreePrevOrder(BTNode* root)
{
if (root == NULL)
{
printf("#");
return;
}
printf("%c", root->data);
BinaryTreePrevOrder(root->left);
BinaryTreePrevOrder(root->right);
}下面的两个接口函数才是最重要的,他要用到我们的队列先进先出的特点,因为C语言没有队列,所以我们需要手搓一个,还好我早有准备,出来吧队列!!!!
#include"Queue.h"
void QueueInit(Queue* pq)
{
assert(pq);
pq->head = pq->tail = NULL;
pq->size = 0;
}
void QueuePush(Queue* pq, QueueDateType x)
{
assert(pq);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
{
perror("malloc fail\n");
exit(-1);
}
newnode->next = NULL;
newnode->val = x;
if (pq->head == NULL)
{
pq->head = pq->tail = newnode;
}
else
{
pq->tail->next = newnode;
pq->tail = newnode;
}
pq->size++;
}
void QueuePop(Queue* pq)
{
assert(pq);
assert(pq->head);
QNode* tmp = pq->head;
pq->head = pq->head->next;
free(tmp);
tmp = NULL;
if(pq->head == NULL)
pq->tail = NULL;
pq->size--;
}
bool QueueEmpty(Queue* pq)
{
assert(pq);
return pq->size == 0;
}
int QueueSize(Queue* pq)
{
assert(pq);
return pq->size;
}
QueueDateType QueueFront(Queue* pq)
{
assert(pq);
return pq->head->val;
}
QueueDateType QueueBack(Queue* pq)
{
assert(pq);
return pq->tail->val;
}
void QueueDestory(Queue* pq)
{
assert(pq);
while (pq->head != pq->tail)
{
QNode* del = pq->head;
pq->head = pq->head->next;
free(del);
}
free(pq->tail);
}这个队列可以放心的使用,那我们就来看看层序遍历上级怎么个事。
void BinaryTreeLevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if(root)
QueuePush(&q, root);
int leafsize = 1;
while (!QueueEmpty(&q))
{
while (leafsize--)
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%c ", front->data);
if (front->left)
QueuePush(&q, front->left);
if (front->right)
QueuePush(&q, front->right);
}
printf("\n");
leafsize = QueueSize(&q);
}
}层序遍历的关键就是这个队列是不是为空,以及队列里有几个数据,所以我们这里必须得做的就是有一个leafsize这个来统计,如果没有这个的话我们无法实现递归的思路,然后最重要的一个就是队列的判空,这个也是特别重要。
那我们层序遍历的思路就是我们把根节点先入进去,出根节点的时候把孩子节点也是插入队列,我们需要一个数字来统计在该层有几个数据,所以这个时候就有了我们leafsize。时刻更新leafsize和入孩子节点就行了。
那大家再来看看我们如何来判断满二叉树的思想。
bool TreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
int levelSize = 1;
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front == NULL)
break;
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
// 前面遇到空以后,后面还有非空就不是完全二叉树
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front)
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}思想就是 :前面遇到空以后,后面还有非空就不是完全二叉树
其实就是如果我们第一次插入根节点,然后每次把孩子带进去,孩子可能是空,空有两种情况一种是到最后为空,一个是最后一层的时候不是满二叉树,后面如果还有节点,队列就不是空,这个时候我们在进行判断一下就可以得出我我们的结果了。
那今天的二叉树就到这里,我们下次再见
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Java API&集合(2)
- python 元组的详细用法
- ansibile 自动化运维实战
- 阿里云服务器 使用Certbot申请免费 HTTPS 证书及自动续期
- 基于Spring Boot、Mybatis、Redis和Layui的企业电子招投标系统源码实现与立项流程
- 服务发现Discovery
- LSKNet:大选择核网络在遥感目标检测中的应用
- 信源、信宿与信道
- Transformers 2023年度回顾 :从BERT到GPT4
- 深思熟虑可能性模型介绍与使用