2024.1.5 关于 二叉平衡树（AVL 树）详解

目录

二叉搜索树

二叉搜索树的简介

二叉搜索树的查找

二叉搜索树的效率

?AVL树

AVL 树的简介

AVL 树的实现

?AVL树的旋转

右单旋

左单旋

左右双旋

右左双旋

完整 AVL树插入代码

验证 AVL 树

AVL 树的性能

---

二叉搜索树

• 要想了解关于二叉平衡树的相关知识，了解二叉搜索树的相关概念是其前提！

二叉搜索树的简介

特点：

• 结点的左子树上所有节点的值都小于该结点的值
• 结点的右子树上所有结点的值都大于该结点的值
• 左右子树也都是二叉搜索树

例图如下：

?

特性：

• 二叉搜索树最左侧节点为最小的节点，最右侧节点为最大的节点
• 采用中序遍历遍历二叉搜索树，能得到一个有序的序列

---

二叉搜索树的查找

• 当根节点为空时，则返回 false
• 当根节点的值等于查询值，则返回 ture
• 当根节点的值小于查询值，则向其左子树进行查找
• 当根节点的值大于查询值，则向其右子树进行查找

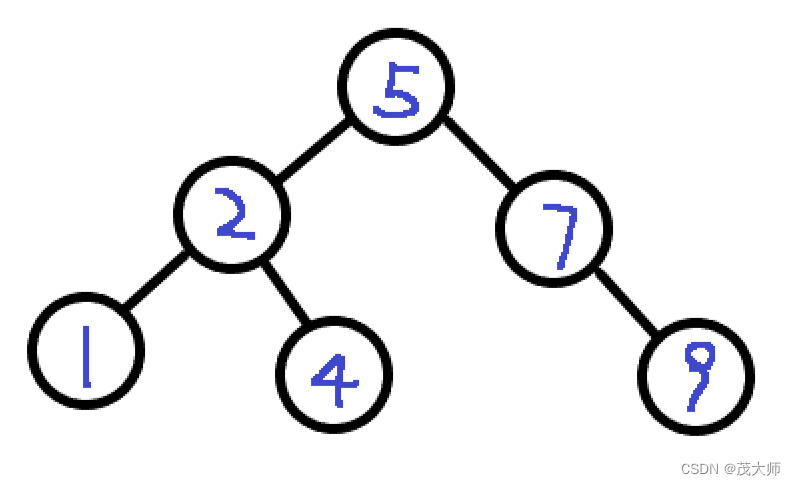
例图如下：

当我们要查询 9 时，其二叉搜索树的查询过程如下：

先由根节点 5 开始，比较其值与查询值，发现 5 < 9?进而查询其右子树

到其右子树根节点，比较其值与查询值，发现 7 < 9 进而查询其右子树

到其右子树根节点，比较其值与查询值，发现 9 = 9，查询完毕 返回 ture

---

二叉搜索树的效率

• 二叉搜索树的平均查找长度与其节点的深度有关，节点越深，则比较次数越多！?

上文例图中我们对数值 9 进行查询，进行了3次比较

下面的例图：同样为6个节点，同样是对9进行查询

根据上文二叉搜索树的查找方式，我们会发现其进行了 6 次比较

显然节点的插入次序不同，得到的二叉搜索树也会不同，导致当对同样的数值进行查找时，其效率也会有较大相差

最优情况：

该二叉搜索树树为二叉完全树，平均的比较次数为：log2N

最坏情况：

该二叉搜索树树为单枝树，平均的比较次数为：N/2

?AVL树

• 当想避免二叉搜索树最坏情况出现时，AVL 树便是优化后的二叉搜索树！

AVL 树的简介

特点：

• 结点的左子树上所有节点的值都小于该结点的值
• 结点的右子树上所有结点的值都大于该结点的值
• 其左右子树的高度差（平衡因子）的绝对值不超过 1
• 左右子树也都是 AVL 树

例图如下：

优点：

• 可以有效的降低树的高度，不会出现像单枝树这样的极端情况，有效的减少平均查找次数

---

AVL 树的实现

1. 定义 AVL 树：

• 首先我们创建一个 TreeNode?静态类，将 AVL 树的相关属性定义完成

public class AVLTree {
    static class TreeNode {
        public int val;
        public int bf;//平衡因子 这里的平衡因子我们是 右子树高度-左子树高度
        public TreeNode left;//左孩子的引用
        public TreeNode right;//右孩子的引用 
        public TreeNode parent;//父亲节点的引用 

//        构造方法
        public TreeNode(int val) {
            this.val=val;
        }

    }
    public TreeNode root;//根节点
}

2. 插入新结点：

• 第一步：先按照二叉搜索树插入结点方式进行新结点的插入

    public boolean insert(int val) {
//        根据传来的参数，创建一个新结点
        TreeNode node = new TreeNode(val);
//        判断根结点是否为空,为空则代表 AVL 树为空,直接将新插入的结点作为根结点即可
        if(root == null ){
            root = node;
            return true;
        }
//        创建一个 cur 结点,利用该结点去遍历这个树的结点
        TreeNode cur = root;
        //创建一个 parent 结点,该结点记录 cur 的父亲结点
        TreeNode parent = null;
//        创建该循环的目的是为了根据新增结点的值，来找到属于它应该插入的位置,当 cur == null 时，退出循环 且 parent 为新插入结点的父亲结点
        while (cur != null){
            if(cur.val > val) {
//                如果 cur 所指向的结点的值大于新增加结点的值，则向左寻找
                parent = cur;
                cur = cur.left;
            }else if (cur.val == val) {
//                新插入结点的值与 cur 所指向的结点的值相等,表示 AVL 树已有一个值与之相等的结点,因为 AVL 树中每个结点的值必须是唯一的,从而不必再插入一个重复值的结点
                return false;
            }else { 
//                如果 cur 所指向的节点的值小于新增加结点的值，则向右寻找
                parent = cur;
                cur = cur.right;
            }
        }
//        走到这说明 cur == null,意思是已经找到了新结点需要插入的位置,且 parent 结点已经记录到了 新结点的父亲结点 的位置
        if (parent.val > val){
            parent.left = node;
        }else {
            parent.right = node;
        }
        return true;
    }

• 第二步：根据插入结点后平衡因子的变化，对该树进行相应的调整，维持平衡因子的绝对值为 1

情况一：parent 结点平衡因子的绝对值为 0，该树无需调整

情况二：parent 结点平衡因子的绝对值为 1，该树不一定平衡，需向上继续查看结点，检查其平衡因子的绝对值

情况三：parent 结点平衡因子的绝对值为 2，该树一定不平衡，根据实际情况，对该树进行相应调整

• 结合上述三种情况我们可以先写出代码的大致框架，至于如何对树进行调整则有好几种情况

    public boolean insert(int val) {
        TreeNode node = new TreeNode(val);
        if(root == null ){
            root = node;
            return true;
        }
        TreeNode cur = root;
        TreeNode parent = null;
        while (cur != null){
            if(cur.val > val) {
                parent = cur;
                cur = cur.left;
            }else if (cur.val == val) {
                return false;
            }else {
                parent = cur;
                cur = cur.right;
            }
        }
        if (parent.val > val){
            parent.left = node;
        }else {
            parent.right = node;
        }

//        这里定义一下新结点的父亲结点为 parent
        node.parent = parent;
//        因为上段代码 cur == null，所以指定一下 cur 指向 node 结点，好为后面平衡因子的调整做准备
        cur = node;

//        根据平衡因子进行树的调整
//        当 parent == null 时，说明 parent 已经爬到该树的根节点之上了，也就是调整完该树了
        while (parent != null) {
            if (cur == parent.right) {
//                新增结点在右树
                parent.bf++;
            }else {
//                新增结点在左树
                parent.bf--;
            }
//          在这里检查 parent 结点平衡因子绝对值的值
            if(parent.bf == 0) {
//            这里说明已经平衡了，无需调整
            }else if(parent.bf == 1 || parent.bf == -1) {
//            虽然 parent 结点是平衡的，但是还需向上查看结点，因为有可能不平
                cur = parent;
                parent = cur.parent;
            }else {
//            这里说明 parent 的平衡因子的绝对值为 2 了,该树必不平衡
                if (parent.bf == 2) {
                    if (cur.bf == 1) {

                    }else {
//                    这里是 cur.bf == -1
                    }
                }else {
//                这里是 parent.bf == -2
                    if (cur.bf == -1) {

                    }else {
//                    这里是 cur.bf == 1
                    }
                }
            }  
        } 
        return true;
    }

?AVL树的旋转

右单旋

具体解析：

• 5结点 为新插入结点

代码：

• 看图理解代码相应含义

private void rotateRight(TreeNode parent) {
        TreeNode subL = parent.left;
        TreeNode subLR = subL.right;
        parent.left = subLR;
        subL.right = parent;
        subLR.parent = parent;
        parent.parent = subL;
    }

• 当然上述仅是 60结点 作为根结点的情况，还有 60结点 不为根结点的情况也许考虑到

更新代码：

private void rotateRight(TreeNode parent) {
        TreeNode subL = parent.left;
        TreeNode subLR = subL.right;
        parent.left = subLR;
        subL.right = parent;
        subLR.parent = parent;
//        这里必须先记录下 parent 的父亲结点
        TreeNode pParent = parent.parent;
        parent.parent = subL;
//        检查 parent 是否为根结点
        if(parent == root) {
            root = subL;
            root.parent = null;
        }else {
//            此时parent 是都父亲节点的，从而需要判断 parent是左子树的还是右子树的
            if(pParent.left == parent) {
                pParent.left = subL;
            }else {
                pParent.right = subL;
            }
            subL.parent = pParent;
        }
    }

• 当然右单旋完树之后还需要，调节其他结点的平衡因子

更新代码：

private void rotateRight(TreeNode parent) {
        TreeNode subL = parent.left;
        TreeNode subLR = subL.right;
        parent.left = subLR;
        subL.right = parent;
        subLR.parent = parent;
//        这里必须先记录下 parent 的父亲结点
        TreeNode pParent = parent.parent;
        parent.parent = subL;
//        检查 parent 是否为根结点
        if(parent == root) {
            root = subL;
            root.parent = null;
        }else {
//            此时parent 是都父亲节点的，从而需要判断 parent是左子树的还是右子树的
            if(pParent.left == parent) {
                pParent.left = subL;
            }else {
                pParent.right = subL;
            }
            subL.parent = pParent;
        }
//        更新上图两个结点的平衡因子
        subL.bf = 0;
        parent.bf = 0;
    }

• 当然我们上述思路中，还有一个问题没有考虑到，就是 subLR 可能为空

最终代码：

• 此代码为完整右单旋逻辑代码

private void rotateRight(TreeNode parent) {
        TreeNode subL = parent.left;
        TreeNode subLR = subL.right;
        parent.left = subLR;
        subL.right = parent;
//        如果 subLR 不为 null，我们才执行，该行代码
        if(subLR != null){
            subLR.parent = parent;
        }
//        这里必须先记录下 parent 的父亲结点
        TreeNode pParent = parent.parent;
        parent.parent = subL;
//        检查 parent 是否为根结点
        if(parent == root) {
            root = subL;
            root.parent = null;
        }else {
//            此时parent 是都父亲节点的，从而需要判断 parent是左子树的还是右子树的
            if(pParent.left == parent) {
                pParent.left = subL;
            }else {
                pParent.right = subL;
            }
            subL.parent = pParent;
        }
//        更新上图两个结点的平衡因子
        subL.bf = 0;
        parent.bf = 0;
    }

---

左单旋

• 代码上左单旋和右单旋逻辑上是一样的，可参照着右单旋代码写

最终代码：

• 此代码为完整左单旋逻辑代码

private void rotateLeft(TreeNode parent) {
        TreeNode subR = parent.right;
        TreeNode subRL = subR.left;
        parent.right = subRL;
        subR.left = parent;
        if(subRL != null) {
            subRL.parent = parent;
        }
        TreeNode pParent = parent.parent;
        parent.parent = subR;
        if (root == parent) {
            root = subR;
            root.parent = null;
        }else {
            if (pParent.left == parent){
                pParent.left = subR;
            }else {
                pParent.right = subR;
            }
            subR.parent = pParent;
        }
        subR.bf = 0;
        parent.bf = 0;
    }

---

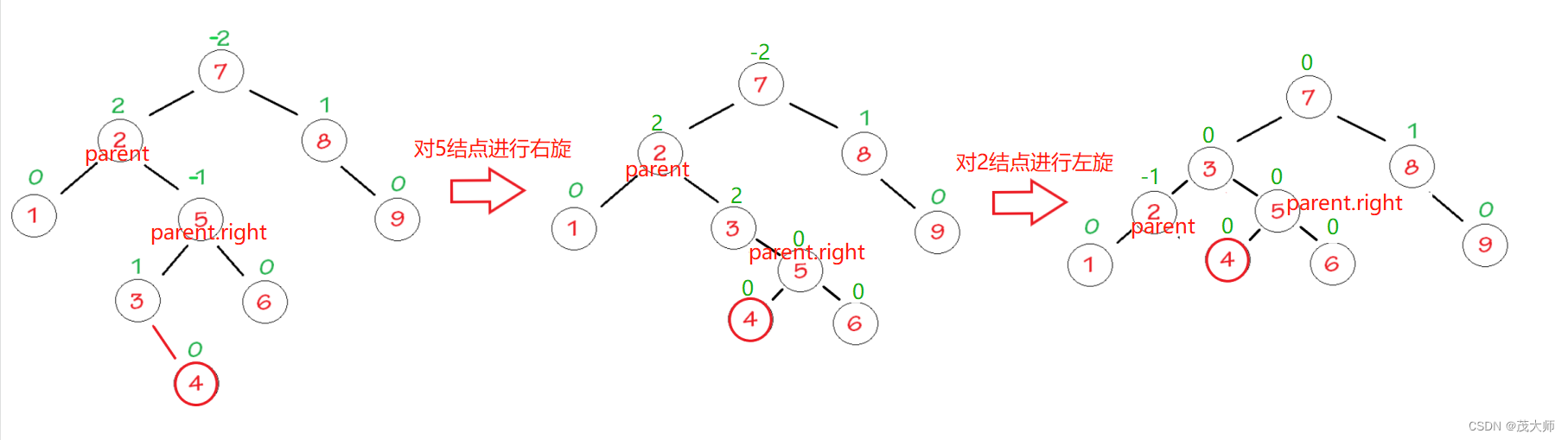
左右双旋

代码：

• 看图理解代码相应含义

    private void rotateLR(TreeNode parent) {
//        先左旋后右旋
        rortateLeft(parent.left);
        rortateRight(parent);
    }

• 当然左右双旋完树之后还需要，调节其他结点的平衡因子

最终代码：

• 此代码为完整左右双旋逻辑代码

private void rotateLR(TreeNode parent) {
        TreeNode subL = parent.left;
        TreeNode subLR = subL.right;
        int bf = subLR.bf;
//        先左旋后右旋
        rotateLeft(parent.left);
        rotateRight(parent);
//        明确一点，当 bf 为 0 时，本身就是平衡的，无需再修改平衡因子
        if(bf == -1){
            subL.bf = 0;
            subLR.bf = 0;
            parent.bf = 1;
        }else if(bf == 1){
            subL.bf = -1;
            subLR.bf = 0;
            parent.bf = 0;
        }
    }

---

右左双旋

最终代码：

• 此代码为完整左右双旋逻辑代码

private void rotateRL(TreeNode parent) {
        TreeNode subR = parent.right;
        TreeNode subRL = subR.left;
        int bf = subRL.bf;
        rotateRight(parent.right);
        rotateLeft(parent);
        if(bf == -1){
            parent.bf = -1;
            subR.bf = 0;
            subRL.bf = 0;
        }else if(bf == 1){
            parent.bf = 0;
            subR.bf = 1;
            subRL.bf = 0;
        }
    }

完整 AVL树插入代码

• 我们将这四种旋转填入到相对应的位置

public boolean insert(int val) {
        //根据传来的参数，创建一个新结点
        TreeNode node = new TreeNode(val);
//        判断根结点是否为空,为空则代表 AVL 树为空,直接将新插入的结点作为根结点即可
        if(root == null ){
            root = node;
            return true;
        }
//        创建一个 cur 结点,利用该结点去遍历这个树的结点
        TreeNode cur = root;
        //创建一个 parent 结点,该结点记录 cur 的父亲结点
        TreeNode parent = null;
//        创建该循环的目的是为了根据新增结点的值，来找到属于它应该插入的位置,当 cur == null 时，退出循环 且 parent 为新插入结点的父亲结点
        while (cur != null){
            if(cur.val > val) {
//                如果 cur 所指向的结点的值大于新增加结点的值，则向左寻找
                parent = cur;
                cur = cur.left;
            }else if (cur.val == val) {
//                新插入结点的值与 cur 所指向的结点相等,表示 AVL 树已有一个值与之相等的结点,因为 AVL 树中每个结点的值必须是唯一的,从而不必再插入一个重复值的结点
                return false;
            }else {
//                如果 cur 所指向的节点的值小于新增加结点的值，则向右寻找
                parent = cur;
                cur = cur.right;
            }
        }
//        走到这说明 cur == null,意思是已经找到了新结点需要插入的位置,且 parent 结点已经记录到了 新结点的父亲结点 的位置
        if (parent.val > val){
            parent.left = node;
        }else {
            parent.right = node;
        }

//        这里定义一下新结点的父亲结点为 parent
        node.parent = parent;
//        因为上段代码 cur == null，所以指定一下 cur 指向 node 结点，好为后面平衡因子的调整做准备
        cur = node;

//        根据平衡因子进行树的调整
//        当 parent == null 时，说明 parent 已经爬到该树的根节点之上了，也就是调整完该树了
        while (parent != null) {
            if (cur == parent.right) {
//                新增结点在右树
                parent.bf++;
            }else {
//                新增结点在左树
                parent.bf--;
            }
//          在这里检查 parent 结点平衡因子绝对值的值
            if(parent.bf == 0) {
//            这里说明已经平衡了，无需调整
            }else if(parent.bf == 1 || parent.bf == -1) {
//            虽然 parent 结点是平衡的，但是还需向上查看结点，因为有可能不平
                cur = parent;
                parent = cur.parent;
            }else {
//            这里说明 parent 的平衡因子的绝对值为 2 了,该树必不平衡
                if (parent.bf == 2) {
                    if (cur.bf == 1) {
//                        这里进行左旋
                        rotateLeft(parent);
                    }else {
//                    这里是 cur.bf == -1,进行右左双旋
                        rotateRL(parent);
                    }
                }else {
//                这里是 parent.bf == -2
                    if (cur.bf == -1) {
//                        这里进行右旋
                        rotateRight(parent);
                    }else {
//                    这里是 cur.bf == 1,进行左右双旋
                        rotateLR(parent);
                    }
                }
//                注意：只要进行过一次旋转，该树便会平衡，无需继续该 while 循环
                break;
            }
        }
        return true;
    }

验证 AVL 树

两条性质：

• 中序遍历 AVL 树可以得到一个有序序列
• 每个结点子树高度差的绝对值不超过 1

代码：

//    验证是否平衡
    public boolean isBalanced(TreeNode root) {
        if(root == null) {
            return true;
        }
        int leftH = height(root.left);
        int rightH = height(root.right);
        if(rightH - leftH != root.bf) {
            System.out.println("结点：" + root.val + "的平衡因子异常");
            return false;
        }
        return Math.abs(leftH - rightH) <= 1 &&
               isBalanced(root.left) &&
               isBalanced(root.right);
    }

//    求树的高度
    private int height(TreeNode root) {
        if(root == null) {
            return 0;
        }
        int leftH = height(root.left);
        int rightH =height(root.right);
        return leftH > rightH ? leftH+1 : rightH+1;
    }

//    验证顺序
    public void dfs(TreeNode root) {
        if (root == null) {
            return;
        }
        dfs(root.left);
        System.out.println("root = " + root.val + "; ");
        dfs(root.right);
    }

AVL 树的性能

优点:

• AVL树是一颗绝对平衡的二叉搜索树，所以能够保证十分高效的查询，其时间复杂度为log2(N)

缺点：

• AVL 树不适合大量的插入和删除，因为要不断的维持AVL树的平衡，从而需要进行大量的旋转

总结：

• 需要高效查询且有序的数据结构，且该数据不会改变，可使用 AVL 树，如果该数据经常发生变化，则不适用于 AVL 树