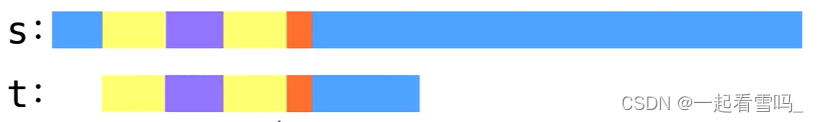字符串匹配的殿堂级算法：KMP算法详解（Java实现版）

目录

KMP的原理

模拟过程1

模拟过程2

KMP算法正确性的简单证明

什么是LPS数组

计算LPS数组

java实现LPS数组

leetcode1392题.最长快乐前缀

java实现KMP算法

---

期末考的小高峰结束咯，我又来写博客啦。今天带来的是历史上第一个线性的字符串匹配算法——KMP算法。

KMP的原理

先举两个字符串进行KMP匹配中的例子。

第一个：

第二个：

上面是两个字串t在与各自的源字符串s匹配过程中t的移动跳跃轨迹，有没有看出什么规律？没有吗，别着急，我再给你上个颜色。

第一个：?

第二个：

是不是有点意思了？第一行源字符串s中，第二个被紫色标记的子串是已匹配部分中和t的部分前缀一样的字串，我们下一次进行匹配时就可以跳过这个子串从下一个字符开始匹配。第一个例子中我们字符A就不用匹配了，第二个例子中我们AB这个字符就不用匹配了，我们都直接从这个子串的后一个字符开始继续去尝试匹配。?

现在我们只是把这个规律给找出来，至于为什么要这样做，为什么这样是正确的我们稍后再讲。我们先给一个定义，这种既是前缀也是后缀的子串我们叫border（非自身性，非空性）。

模拟过程1

我们来模拟一下这个匹配的过程。s串中用i来代表索引的移动，t串中用j来代表索引的移动。

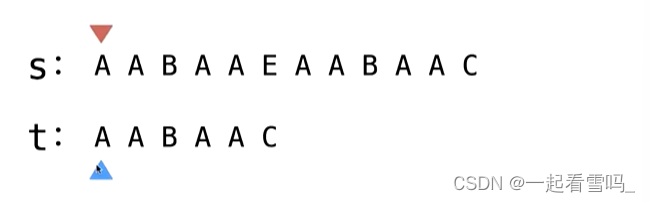
当我们到了s串中E的位置时，我们发现和t串不匹配了，我们就开始寻找s串中已匹配部分中border的位置，即寻找那个既是前缀也是后缀的字串。?

我们发现在这个字符串中，border有两种，A或者AA，这种情况下我们关心的是最长的那个。于是我们要从AA的下一个位置继续进行匹配。

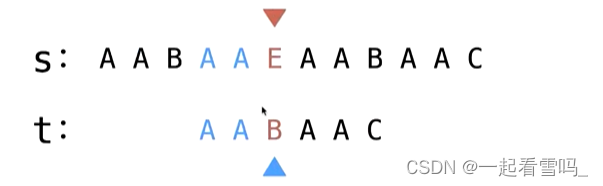我们为什么要关心最长的那个border呢？我们来想象一下，如果我们关心短的那个border的话，我们t串跳的位置就如下图所示。

?

我们发现它比我们AA作为border跳的要靠后， 这种情况下我们就有可能漏掉解，因为我们跳过了一些字符没进行匹配，考虑最长的border保证了重合的部分尽可能长，保证不漏掉解。这一点我们下面还会进一步解释。

模拟过程2

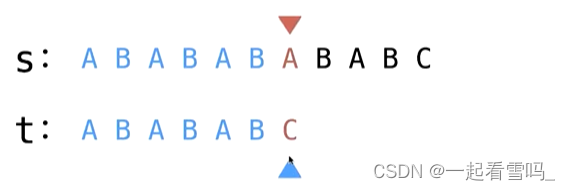
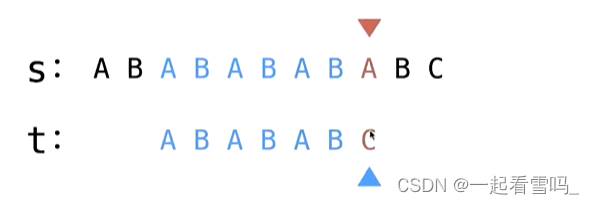
我们发现这个字符串也有两个border，AB和ABAB。如刚才所说，我们关注最长的ABAB。

?

?

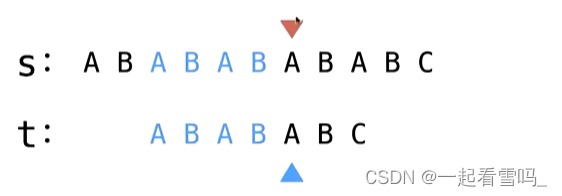
这个模拟主要是想说明在已匹配的部分ABAB有重叠没关系，只要保证既是前缀也是后缀就好了。?如果没太看懂什么叫重叠没关系，下文的简单证明中有进一步说明。

为了实现KMP算法，我们就需要弄明白如何计算出最长的border，我们先来证明一下为什么这样做是正确的。

KMP算法正确性的简单证明

首先是需要在s中找到和t完美匹配的字串。?

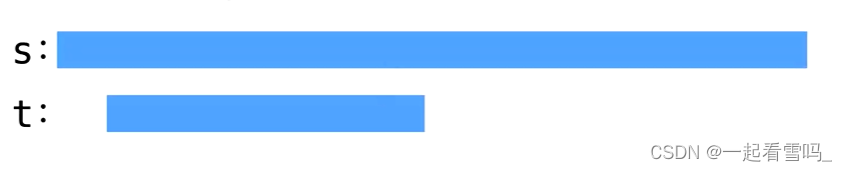
?紫色表示匹配成功的部分，红色表示匹配失败的部分。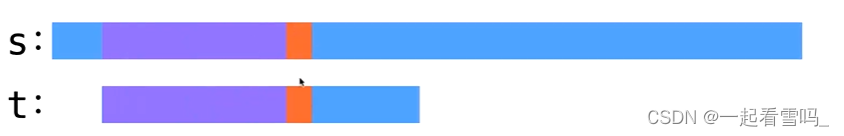

找到匹配成功的紫色部分中最长的border，标为黄色部分。为了表示清晰，我们这里两个黄色的部分是不重叠的，有一小段紫色把它们隔开了，即使是重叠的也没关系，上文的模拟过程2已经讲过了。

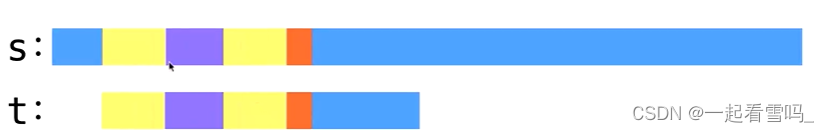
?直接从红色的字符继续匹配。

为什么考虑最长的border是向前移动最少的方案？

我们需要证明最长的border使匹配不会漏掉解，让我们用反证法假设在更早的地方能匹配到解。

假设我们在已知的最长的黄色border前的绿色位置就匹配成功了 ，从绿色部分开始出发往后都匹配成功了。

把我们t串的黄色部分往后延展一下，反正都匹配成功了。?

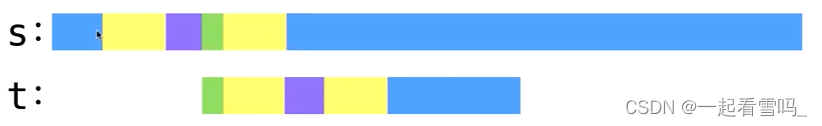?把s串开头部分对应上绿色，这时候我们发现我们找到了一个由绿色和黄色组成的更长的border，这和我们的前提黄色是最长的border矛盾了，由此得证。

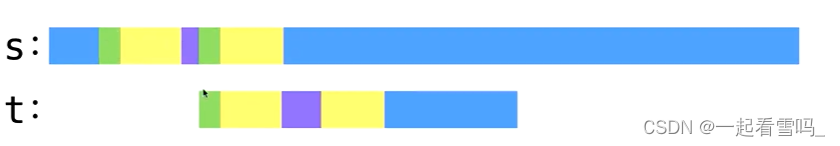
什么是LPS数组

s和t在匹配过程中，前面几个前缀都匹配成功，在红色部分匹配失败。

我们需要计算t的每一个前缀的最长的border，所以我们计算的不是一个值，而是一组值。我们把这些值存在LPS数组中，LPS（Longest proper Prefix which is also Suffix）的中文含义就是非空的、不是自身的、最长的、既是前缀也是后缀的子串。

我们来具体的举个例子看看LPS数组。

当只有一个字符A时，它无法充当自己的border，所以LPS数组对应的值为0。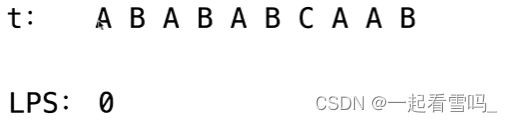来到B，B这里存储的是AB这个前缀的border，从A开始看，A != B，再往后走就又是AB这个子串本身了，所以存储的值也是0。

到了下一个A，ABA对应的最长的既是前缀也是后缀的border为A，长度是1，对应的LPS的值也就是1。

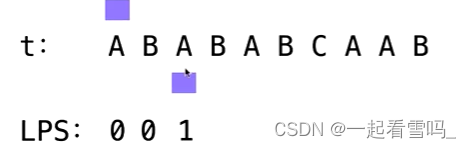
到了ABAB这个前缀，最长的border为AB，长度为2，对应的LPS值为2。?

?

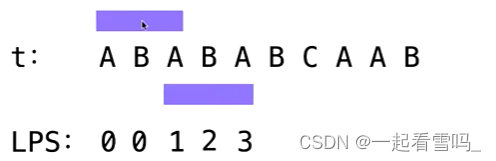
到了ABABA这个前缀，最长的border为ABA，长度是3，对应的LPS数组值就是3。?

?

以此类推计算t的每一个前缀中最长的border，我们给出最终的结果。

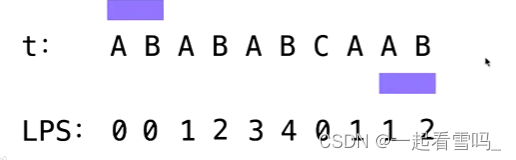有了LPS这个数组存储每一个前缀中最长的border，我们在让s和t匹配的时候，不管前缀是多少的时候匹配失败的，我们都可以直接快速的找到下一次比较的位置。

什么是LPS数组

s和t在匹配过程中，前面几个前缀都匹配成功，在红色部分匹配失败。

我们需要计算t的每一个前缀的最长的border，所以我们计算的不是一个值，而是一组值。我们把这些值存在LPS数组中，LPS（Longest proper Prefix which is also Suffix）的中文含义就是非空的、不是自身的、最长的、既是前缀也是后缀的子串。

我们来具体的举个例子看看LPS数组。

当只有一个字符A时，它无法充当自己的border，所以LPS数组对应的值为0。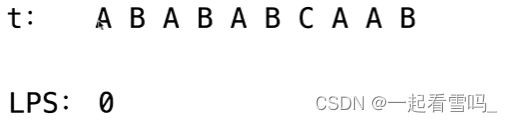来到B，B这里存储的是AB这个前缀的border，从A开始看，A != B，再往后走就又是AB这个子串本身了，所以存储的值也是0。

到了下一个A，ABA对应的最长的既是前缀也是后缀的border为A，长度是1，对应的LPS的值也就是1。

到了ABAB这个前缀，最长的border为AB，长度为2，对应的LPS值为2。?

?

到了ABABA这个前缀，最长的border为ABA，长度是3，对应的LPS数组值就是3。?

?

以此类推计算t的每一个前缀中最长的border，我们给出最终的结果。

有了LPS这个数组存储每一个前缀中最长的border，我们在让s和t匹配的时候，不管前缀是多少的时候匹配失败的，我们都可以直接快速的找到下一次比较的位置。

计算LPS数组

LPS[i - 1] = a意思是i前面的前缀中（也就是从0到i - 1索引的位置这段前缀）最长的border的长度为a，LPS[0]的值肯定为0，因为我们对border的定义就说了border不能是前缀本身。我们现在希望能通过LPS[i - 1]的值推出LPS[i]的值，也就是从LPS[0]开始递推出LPS[1] 、LPS[2].....

黄色子串表示已匹配的前缀中最长的border，t[a]是第一个黄色子串的下一个字符（因为黄色子串长度为a，而数组的索引从0开始），t[i]是第二个黄色子串的下一个字符，如果二者相等就递推出了LPS[i] 的值（也就是索引从0到i这段前缀中的border值）为 a + 1。LPS[i] 比 LPS[i - 1]最多大1。

那如果二者不相等呢？LPS[i]就是0吗？

不是的，我们来举个例子。

索引所在的B前面的前缀ABACABA的LPS值为3，由刚才的递推方法，我们发现ABA这个值为3的border并不是B所在的前缀ABACABAB的border，我们这个最长的border匹配失败了，我们就去看次长的border，看次次长的border....很显然除了ABA这个长度为3的border，还有AB这个长度为2的border和B所在的前缀匹配成功了，于是我们这个前缀的最长的border为2。

也就是最长的border的t[i]和t[a]匹配失败后我们就看次长的border，假设我们次长的border为下图绿色部分，如果这个次长的border匹配成功的话，那么这个border就是索引所在的前缀的最长的border。绿色的部分是黄色部分的前缀也是后缀，也是黄色部分最长的，那么a = LPS[a - 1]看t[a]，不断地更新a的值。

java实现LPS数组

leetcode1392题.最长快乐前缀

1392. 最长快乐前缀 - 力扣（LeetCode）?

「快乐前缀」?是在原字符串中既是?非空?前缀也是后缀（不包括原字符串自身）的字符串。

给你一个字符串?s，请你返回它的?最长快乐前缀。如果不存在满足题意的前缀，则返回一个空字符串?""?。

示例 1：

输入：s = "level"
输出："l"
解释：不包括 s 自己，一共有 4 个前缀（"l", "le", "lev", "leve"）和 4 个后缀（"l", "el", "vel", "evel"）。最长的既是前缀也是后缀的字符串是 "l" 。

示例 2：

输入：s = "ababab"
输出："abab"
解释："abab" 是最长的既是前缀也是后缀的字符串。题目允许前后缀在原字符串中重叠。提示：

• 1 <= s.length <= 105
• s?只含有小写英文字母

class Solution {
    public String longestPrefix(String s) {
       int []lps = getLPS(s);
       int len = lps[s.length() - 1];
       //java的substring是前闭后开的
       return s.substring(0, len);
    }
    private int[]getLPS(String t){
        int [] lps = new int[t.length()];
        //lps每个值怎么求
        for(int i = 1; i < t.length(); i++){
            int a = lps[i - 1];
            while(a > 0 && t.charAt(i) != t.charAt(a)){
                a =lps[a - 1];
            }
            if(t.charAt(i) == t.charAt(a)){
                lps[i] = a + 1;
            }
        }
        return lps;
    }
}

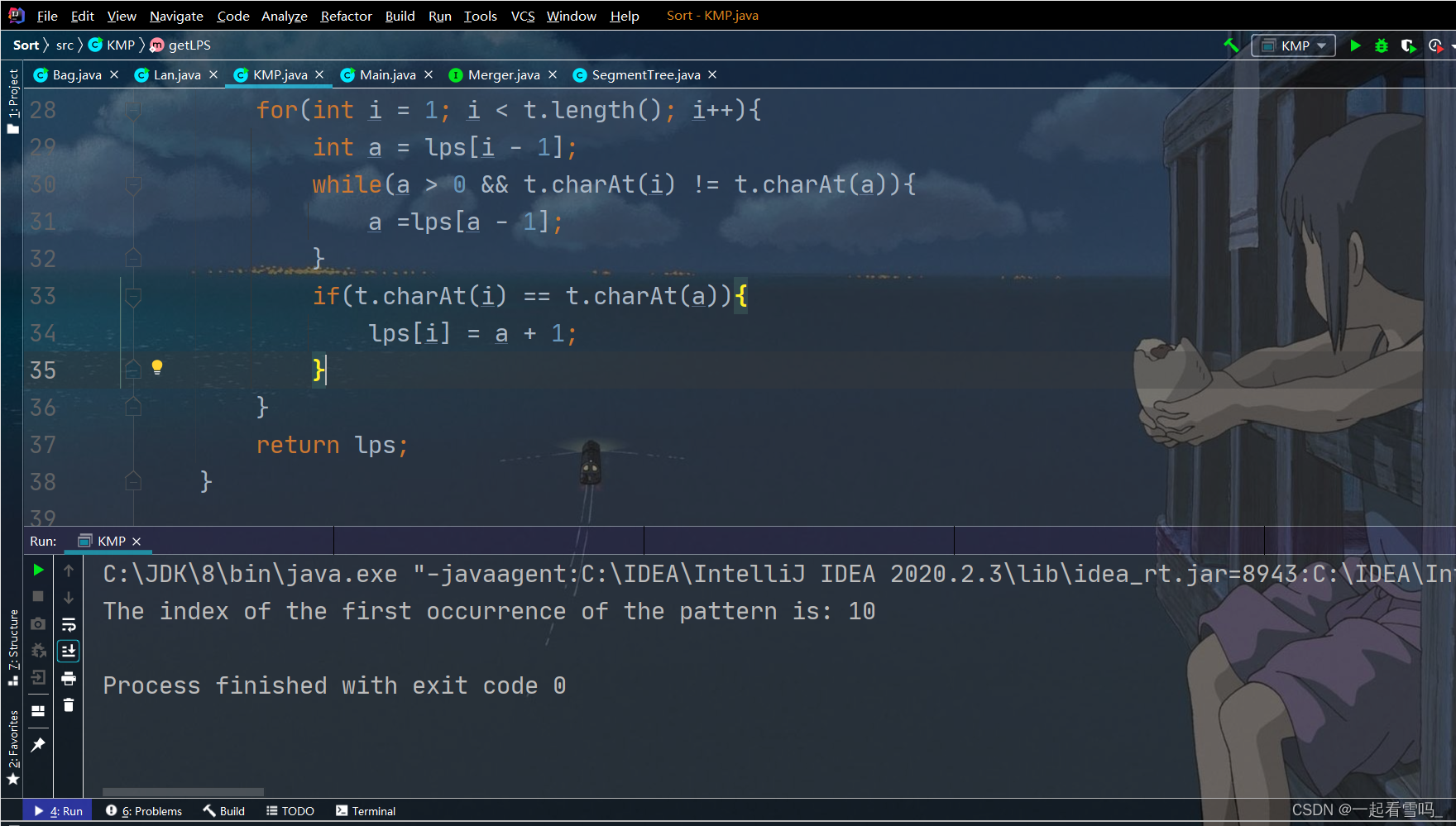
java实现KMP算法

public class KMP {
    public static int kmp(String s, String t){
        if(s.length() < t.length()) return -1;
        if(t.length() == 0) return 0;

        int []lps = getLPS(t);
        int i = 0, j = 0;
        while(i < s.length()){
            if(s.charAt(i) == t.charAt(j)){
                i++;
                j++;
                if(j == t.length()){
                    return i - t.length();
                }
            }
            else if(j > 0){
               j = lps[j - 1];
            }
            else {
                i++;
            }
        }
        return -1;
    }
    private static int[]getLPS(String t){
        int [] lps = new int[t.length()];
        //lps每个值怎么求
        for(int i = 1; i < t.length(); i++){
            int a = lps[i - 1];
            while(a > 0 && t.charAt(i) != t.charAt(a)){
                a =lps[a - 1];
            }
            if(t.charAt(i) == t.charAt(a)){
                lps[i] = a + 1;
            }
        }
        return lps;
    }

    public static void main(String[]args){
        String s = "ABABDABACDABABCABAB";
        String t = "ABABCABAB";
        int result = kmp(s, t);
        System.out.println("The index of the first occurrence of the pattern is: " + result);
      }
}