对角矩阵,投影矩阵,三角矩阵的特征值性质
目录
一. 引入
对于如下的微分方程:
其解肯定类似指数形式,如下:
其中为特征值,决定函数增长还是衰减;x为特征向量,决定函数增长/衰减的速率。这种微分方程的解一般不只一个,对所有的解进行组合也是对的。最后再根据初始值条件确定常数的值,即为最终的答案。
矩阵特征值与特征向量满足:
Ax代表对向量x进行转变,如果这种转变不改变向量x的方向,则出现了特征向量。矩阵的对角化可以反应这种性质。
矩阵对角化的思路被广泛应用于微分方程,斐波纳契数(Fibonacci number),马尔科夫链,网络安全等领域。对角化的过程离不开计算特征值与特征向量。对于不能对角化的矩阵,我们将其称作缺陷矩阵(defective matrices)。
二. 对角矩阵
2.1 对角矩阵的特征值与特征向量
来看一个二阶的对角矩阵(diagonal matrix):

很容易计算该矩阵拥有两个特征值和两个基本的特征向量,如下:
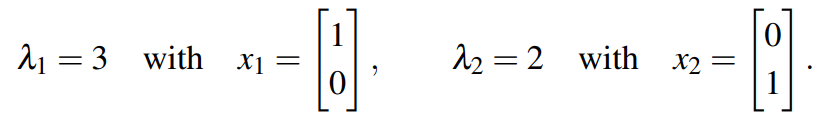
矩阵与特征向量相乘的结果与向量数乘的结果是一样的,也就是:
同理:
对于任意的其他向量,比如说:
可以将其表示成两个特征向量的组合,也就是:
如果将矩阵A与该向量相乘,根据特征值的性质,很容易得到:
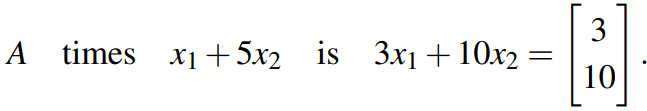
很明显向量x不是该矩阵的特征向量。
2.2 小结
- 对角矩阵的特征值是其对角线处元素的值;
- 特征向量可以形成特征空间来表示其他向量;
三. 投影矩阵
3.1 投影矩阵的特征值与特征向量
举一个二阶的投影矩阵(projection matrix)例子,如下:
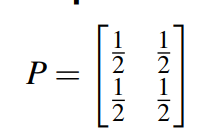
很容易计算出该矩阵的特征值与特征向量,如下:
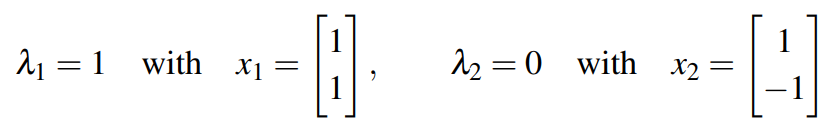
向量x的投影可以是其本身,所以投影矩阵必有特征值1.
代表向量x往0向量上投影。
假定投影矩阵P的列空间(column space)为r,很明显其行空间也为r,零空间(nullspace)为n-r。
那么当特征值为1时,会重复r次,在这个例子中就是重复1次;
当特征值取0时,会重复n-r次,在这个例子中也是重复1次。
需要注意的是,特征值是可以重复的。比如我们来看一个简单的对角阵,如下:
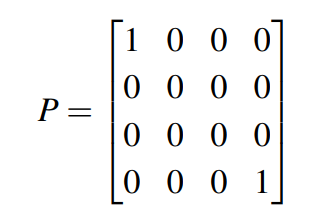
该矩阵则有4个特征值,分别是1,1,0,0。同理可得,该矩阵的列空间为2,零空间为4-2=2.
可以看成平凡的特征值,如下:
也就是此时特征向量x位于A的零空间中。特征值为0的矩阵是奇异的,也就不可求逆,行列式为0.换句话说如果矩阵所有的特征值都非0的话,那么该矩阵则可以求逆。
3.2 小结
- 投影矩阵的特征值只有1和0;
- 投影矩阵特征值1出现的次数与列空间维度一样;
- 投影矩阵特征值0出现的次数与零空间维度一样;
- 特征值为0的矩阵=奇异矩阵=不可逆矩阵=行列式为0;
- 可逆矩阵的特征值不会出现0
四. 三角矩阵
4.1 三角矩阵的特征值与特征向量
根据经验,三角矩阵(triangular)的特征值就是对角线上的元素。比如某三阶矩阵的特征行列式可计算为:
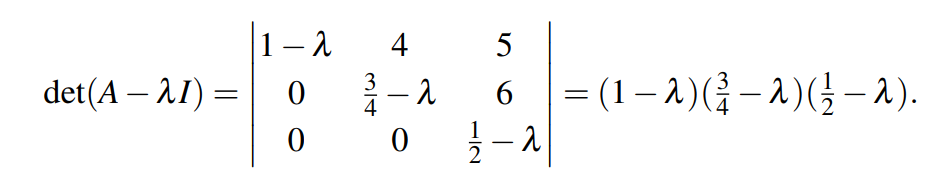
很明显发现此行列式就是对角线元素的乘积。当该行列式为0时,可得特征值为:
特征向量也与矩阵主对角的取值有关。
由此我们发现:
将矩阵转变为对角阵或者三角矩阵,不会改变其特征值
需要注意结论的运用。比如将矩阵A进行高斯分解(Gaussian factorization):
A=LU
其中L为下三角矩阵,U为上三角矩阵。
很明显矩阵U的特征值就是其对角线的元素,但是和矩阵A的特征值大小是不一样的。
4.2 小结
三角矩阵的特征值即为对角线处的元素(不论上三角还是下三角矩阵)
五. 矩阵的迹,行列式,特征值之间的关系
5.1 特征值与求解Ax=b
从计算的角度来说,特征值问题比求解Ax=b要难一些。
对于求解Ax=b来讲,就是一个线性的系统,经过有限的基础行变换就可以在短时间内求出答案。或者直接借助Cramer法则也可以算出结果。
对于求解特征值,有一步到位的公式吗?
Galois和Abel探索了毕生都未能求出结果。举个例子,对于5行5列的矩阵来讲,其特征值多项式会出现特征值的五次方,也就是
。对于5次的多项式,目前还没有代数上的统一求解公式。
5.2 特征值的求和与求积
矩阵特征值的求和就是对角线元素的和,又被称之为矩阵的迹(trace),如下:
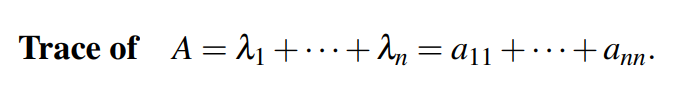
矩阵特征值的积就是行列式的值。
在介绍投影矩阵时,我们举了一个例子P,该矩阵对角线的元素为1/2和1/2,其特征值为1和0,由此满足:
利用特征值的乘积也可以验证投影矩阵为奇异矩阵,行列式为0.反过来,矩阵行列式为0,说明至少存在一个特征值为0
需要注意的是,矩阵的特征值,矩阵对角线元素的值,矩阵的主元(pivot),这三者是完全不同的概念。只有在三角矩阵里面,这些是等效的。
来看一个二阶矩阵的例子:
该矩阵的迹为a+d,行列式为ad-bc
特征多项式可以计算如下:
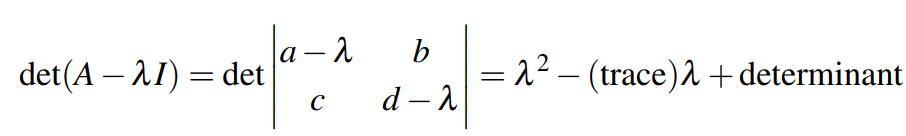
对于该二阶矩阵来讲,特征值,矩阵的迹,行列式的完整关系如下:

很明显可以验证该二阶矩阵两个特征值的和即为矩阵的迹。由此可得:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!