补题与总结：牛客小白月赛83（B~F）

写在最前面的复盘

出了ABCD，犯的最大错误就是读假题，ABE都读假了。赛后一想确实读题太急，也没通过用例验证题意
C是一道简单概率题，可能是高中数学考试填空第一题吧，数学忘的太快，概率这块练的也少，好在最后推出来了
赛时却wa穿了D，没想到正解，用了暴力超时，发现答案的数量远远低于询问的数量，想用记忆化优化，接着wa穿。每次读出一个错误就直接交，然后继续wa，还是太着急了，很多代码的细节没有写好就想着交了。赛后看到正解，将$O(n^2)$的枚举优化到$O(n)$的思路很值得学习
E，$O(n)$找下一个不同字符的下标，用set优化成$O(lngn)$也值得学习
F，补题时wa穿，对于我目前的实力还是略难了，就算赛时能利用题目性质和数据范围推导出结论，最后的代码实现也会漏掉很多细节，因为要考虑很多边界和结论的性质。但总的来说，推导结论的过程还是值得学习的

B-小天的魔法（贪心 模拟 双指针）

B-小天的魔法_牛客小白月赛83 (nowcoder.com)

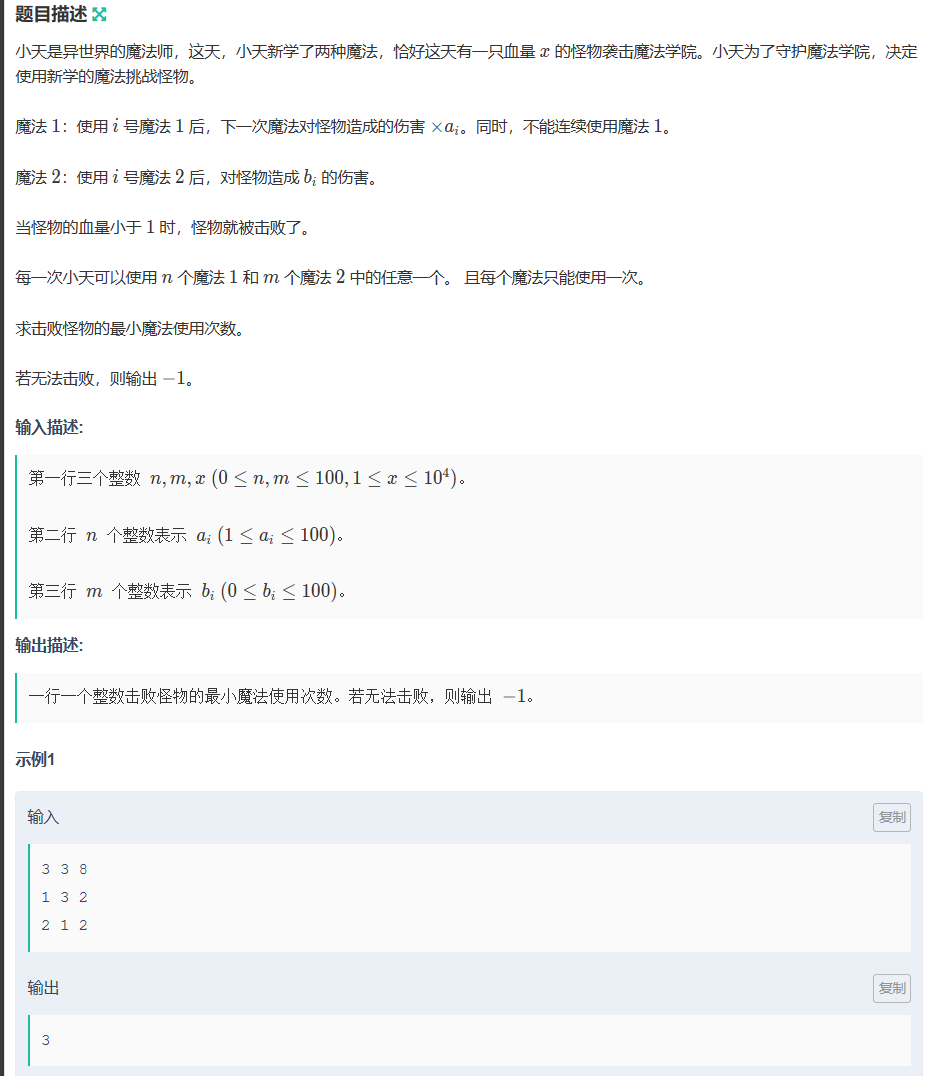
用数组a，b存储题目给定的两个序列，并对其降序排序。用i，j两个指针分别指向a，b数组的第一个元素
贪心思路：考虑使用$b_j$之前是否要使用$a_i$，若$a_i$ != 1，则先使用$a_i$再使用$b_j$
证明：使用次数相同时，比较$a_i?b_j$与$b_j+b_{j+1}$的大小。显然$a_i$不为1时，有以下关系
$$a_i?b_j>=b_j+b_j>=b_j+b_{j+1}$$
显然使用两次b魔法造成的伤害小于等于先使用a再使用b，证明完毕

注意：若直接使用$b_j$就能击败怪物，则直接使用$b_j$

#include <bits/stdc++.h>
using namespace std;

const int N = 3e5 + 10;
int a[N], b[N];

void solve()
{
    int n, m, x; cin >> n >> m >> x;
    for (int i = 1; i <= n; ++ i) cin >> a[i];
    for (int i = 1; i <= m; ++ i) cin >> b[i];
    sort(a + 1, a + n + 1, greater<int>()), sort(b + 1, b + n + 1, greater<int>());
    int i = 1, j = 1;
    int cur = 0, cnt = 0;
    while (j <= m)
    {
        if (cur >= x) break;
        // 直接使用b[j]就能击败怪物
        if (j <= m && cur + b[j] >= x) cur += b[j ++ ], cnt ++ ;
        // 当a[i] != 1时，贪心
        else if (i <= n && a[i] != 1) cnt += 2, cur += a[i ++ ] * b[j ++ ];
        else if (j <= m) cnt ++ , cur += b[j ++ ];
    }
    if (cur >= x) cout << cnt << "\n";
    else cout << "-1\n";
}

int main()
{
    ios::sync_with_stdio(false), cin.tie(0),cout.tie(0);
    solve();
    return 0;
}

---

C-小天的 Minecraft（概率）

C-小天的 Minecraft_牛客小白月赛83 (nowcoder.com)

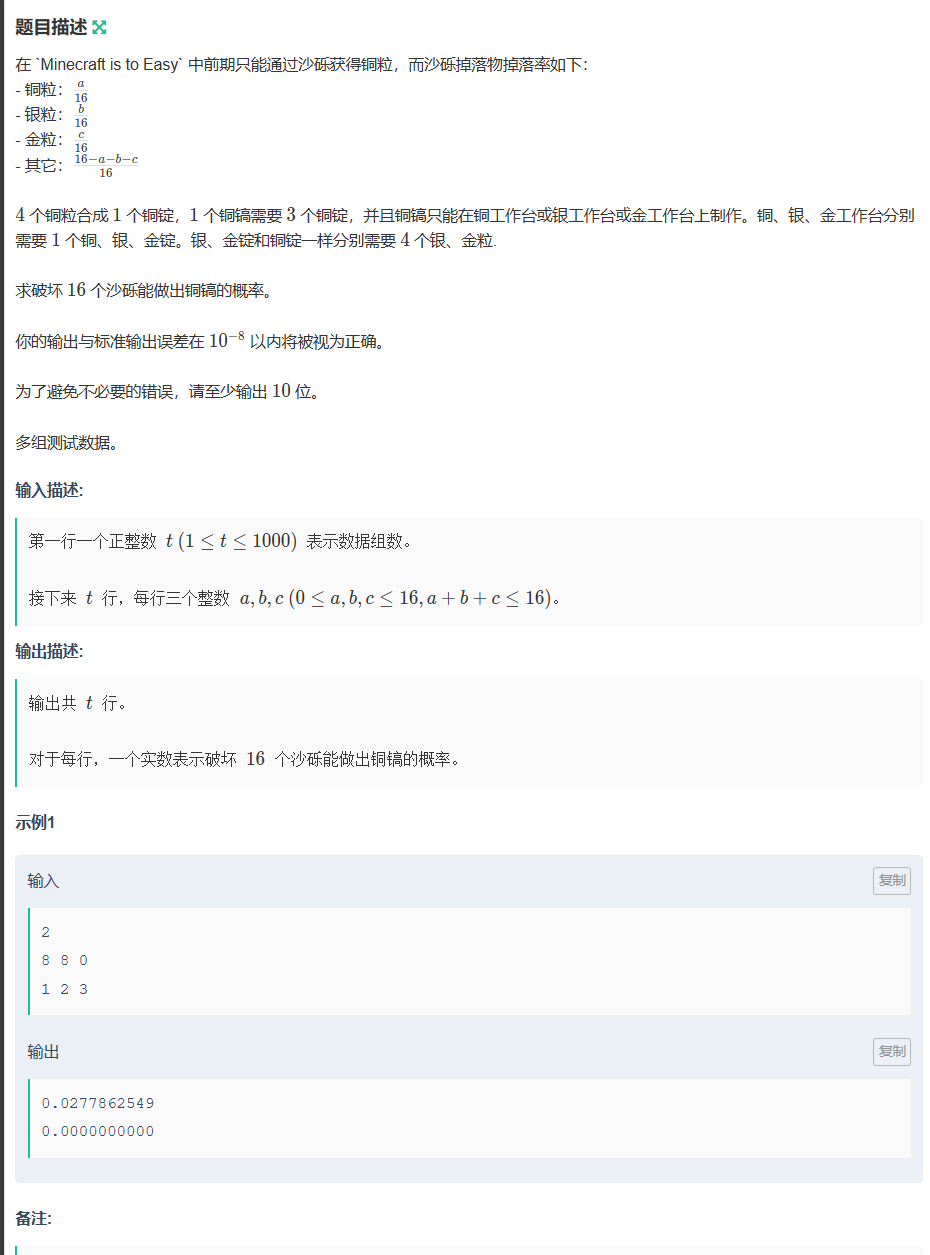
生成铜稿首先要12个铜粒，其次需要一个工作台。工作台有三种情况：铜、银、金
铜工作台需要4个铜粒，银的需要4个银粒，金的需要4个金粒
显然，有三种情况能生成铜稿

• 12个铜粒+铜工作台：16个铜粒
• 12个铜粒+银工作台：12个铜粒+4个银粒
• 12个铜粒+金工作台：12个铜粒+4个金粒

假设事件发生的概率为p，重复m次该事件，发生n次p的概率为：
$$C_m^n?p^n$$
$p_a$、$p_b$、$p_c$分别为掉落铜粒、银粒、金粒的概率，那么以上三种情况的概率为：

• $C_{16}^{16}?p_a^{16}$
• $C_{16}^{12}?p_a^{12}+C_{16}^4?p_b^4$
• $C_{16}^{12}?p_a^{12}+C_{16}^4?p_c^4$

将三种情况的概率相加即为答案（代码丑陋，看思路自己写就行）

#include <bits/stdc++.h>
using namespace std;

void solve()
{
    int T; cin >> T;
    while (T --)
    {
        double a, b, c; cin >> a >> b >> c;
        a /= 16, b /= 16, c /= 16;
        double ans = 1;
        double t = 1;
        for (int i = 0; i < 12; ++ i) t *= a;
        for (int i = 0; i < 16; ++ i) ans *= a;
        double t1 = 1, t2 = 1, t3 = 1;
        for (int i = 0; i < 4; ++ i) t1 *= a, t2 *= b, t3 *= c;
        ans += t * (t2 + t3) * 4 * 5 * 7 * 13; // 4 * 5 * 7 * 13为C_16^4的值
        printf("%.12lf\n", ans);
    }
}

int main()
{
    solve();
    return 0;
}

---

D-小天的子序列（预处理 排列组合）

D-小天的子序列_牛客小白月赛83 (nowcoder.com)

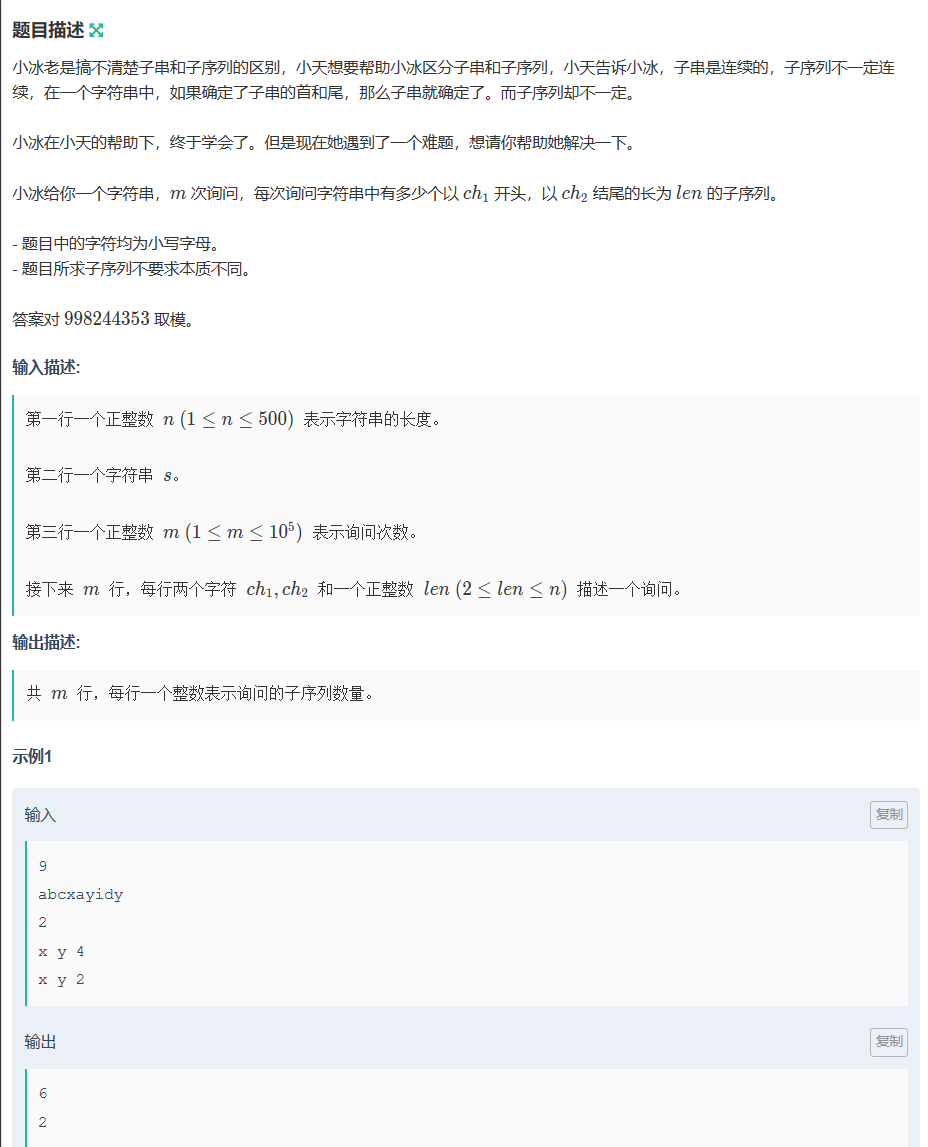
假设以ch1为开头，ch2为结尾的字符串长度为n，那么满足条件的子序列数量为
$$C_{n?2}^{len?2}$$
根据数据范围，需要预处理组合数$C_m^n$，1<=m <=500, 1<=n<=500
模板为：

for (int i = 0; i < N; ++ i) c[i][0] = 1;
for (int i = 1; i < N; ++ i)
	for (int j = 1; j <= i; ++ j)
		c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % 998244353;

接着就是找字符串中的满足条件子串：以ch1为开头，ch2为结尾，且长度大于len
由于字符串最大长度为500，直接暴力预处理字符串所有子串的情况
用cnt[26][26][500]保存所有子串的出现次数，如cnt[0][3][2] = 4表示：整个字符串中，以a(0 = a - a)为开头，以d(3 = d - a)为结尾，且长度为2的子串出现了4次

满足条件的子串为cnt[ch1][ch2][t]，len <= t <= 500
对于每次的询问，线性枚举t满足条件的子串出现次数并乘以组合数即可

注意：组合数的预处理数组最好开LL

#include <bits/stdc++.h>
using namespace std;

const int mod9 = 998244353;
const int N = 510;
long long cnt[30][30][N], c[N][N];

void solve()
{
    int n; cin >> n;
    string s; cin >> s;
    s = " " + s;

    for (int i = 0; i < N; ++ i) c[i][0] = 1;
    for (int i = 1; i < N; ++ i)
        for (int j = 1; j <= i; ++ j)
            c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod9;
    for (int i = 1; i <= n; ++ i)
        for (int j = i + 1; j <= n; ++ j)
            cnt[s[i] - 'a'][s[j] - 'a'][j - i + 1] ++ ;
    int m; cin >> m;    
    while (m --)
    {
        long long ans = 0;
        char x, y; cin >> x >> y;
        int len; cin >> len;
        for (int i = len; i <= n; ++ i)
            ans = (ans + c[i - 2][len - 2] * cnt[x - 'a'][y - 'a'][i]) % mod9;
        cout << ans << "\n";
    }
}

int main()
{
    ios::sync_with_stdio(false), cin.tie(0),cout.tie(0);
    solve();
    return 0;
}

---

E-小天的贪吃蛇（模拟）

E-小天的贪吃蛇_牛客小白月赛83 (nowcoder.com)

模拟蛇的轨迹，将二维数组转换成一维字符串，保存数组下标与字符串下标之间的映射关系，同时用pos数组保存每个字符在字符串的出现位置（下标）。如pos[1]表示字符b (1 = b - a)在数组中的下标，这些下标用set存储，即set pos[26]

对于修改操作，将二维坐标转换成字符串的下标并修改字符串，同时维护pos数组
对于询问操作，也是将二维坐标转换成字符串的下标，并且获取该下标对应字符。此时在其他字符的出现位置中，找出大于等于（lower_bound）该下标的最小下标，两下标之间的距离为答案

#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int> PII;
typedef long long LL;
typedef unsigned long long ULL;
const int inf = 2e9 + 10;
const LL INF = 4e18 + 10;
const int mod9 = 998244353;
const int mod7 = 1e9 + 7;
const int N = 3e5 + 10;
int n, m; 
set<int> pos1[30], pos2[30];

void solve()
{
    cin >> n >> m;
    vector<vector<char>> g(n + 1, vector<char>(m + 1, 0));
    vector<vector<int>> idx1(n + 1, vector<int>(m + 1));
    vector<vector<int>> idx2(n + 1, vector<int>(m + 1));
    
    for (int i = 1; i <= n; ++ i)
        for (int j = 1; j <= m; ++ j)   
            cin >> g[i][j];
    string s1, s2;
    int i = 1, j = 1, dir = 1, cnt = 0;
    while (i <= n)
    {
        s1 += g[i][j], pos1[g[i][j] - 'a'].insert(cnt);
        idx1[i][j] = cnt ++ ;
        j += dir;
        if (j == m + 1) j = m, i ++ , dir *= -1;
        if (j == 0) j = 1, i ++, dir *= -1;
    }
    i = 1, j = 1, dir = 1, cnt = 0;
    while (j <= m)
    {
        s2 += g[i][j], pos2[g[i][j] - 'a'].insert(cnt);
        idx2[i][j] = cnt ++ ;
        i += dir;
        if (i == n + 1) i = n, j ++ , dir *= -1;
        if (i == 0) i = 1, j ++ , dir *= -1;
    }
    int Q; cin >> Q;
    while (Q --)
    {
        int t, x, y; cin >> t >> x >> y;
        if (t == 1)
        {
            char c; cin >> c;
            pos1[s1[idx1[x][y]] - 'a'].erase(idx1[x][y]);
            pos2[s2[idx2[x][y]] - 'a'].erase(idx2[x][y]);            
            s1[idx1[x][y]] = c;
            s2[idx2[x][y]] = c;
            pos1[c - 'a'].insert(idx1[x][y]);
            pos2[c - 'a'].insert(idx2[x][y]);
        }
        else if (t == 2)
        {
            int c = s1[idx1[x][y]] - 'a';
            int ans = inf;
            for (int i = 0; i < 26; ++ i)
                if (i != c)
                {
                    auto it = pos1[i].lower_bound(idx1[x][y]);
                    if (it != pos1[i].end())
                        ans = min(ans, *it);
                    else ans = min(ans, n * m);
                }
            cout << ans - idx1[x][y] << "\n";
        }
        else
        {
            int c = s2[idx2[x][y]] - 'a';
            int ans = inf;
            for (int i = 0; i < 26; ++ i)
                if (i != c)
                {
                    auto it = pos2[i].lower_bound(idx2[x][y]);
                    if (it != pos2[i].end())
                        ans = min(ans, *it);
                    else ans = min(ans, n * m);
                }
            cout << ans - idx2[x][y]  << "\n";
        }
    }
}

int main()
{
    ios::sync_with_stdio(false), cin.tie(0),cout.tie(0);
    solve();
    return 0;
}

---

F-小天的 A+B（结论题）

F-小天的 A+B_牛客小白月赛83 (nowcoder.com)

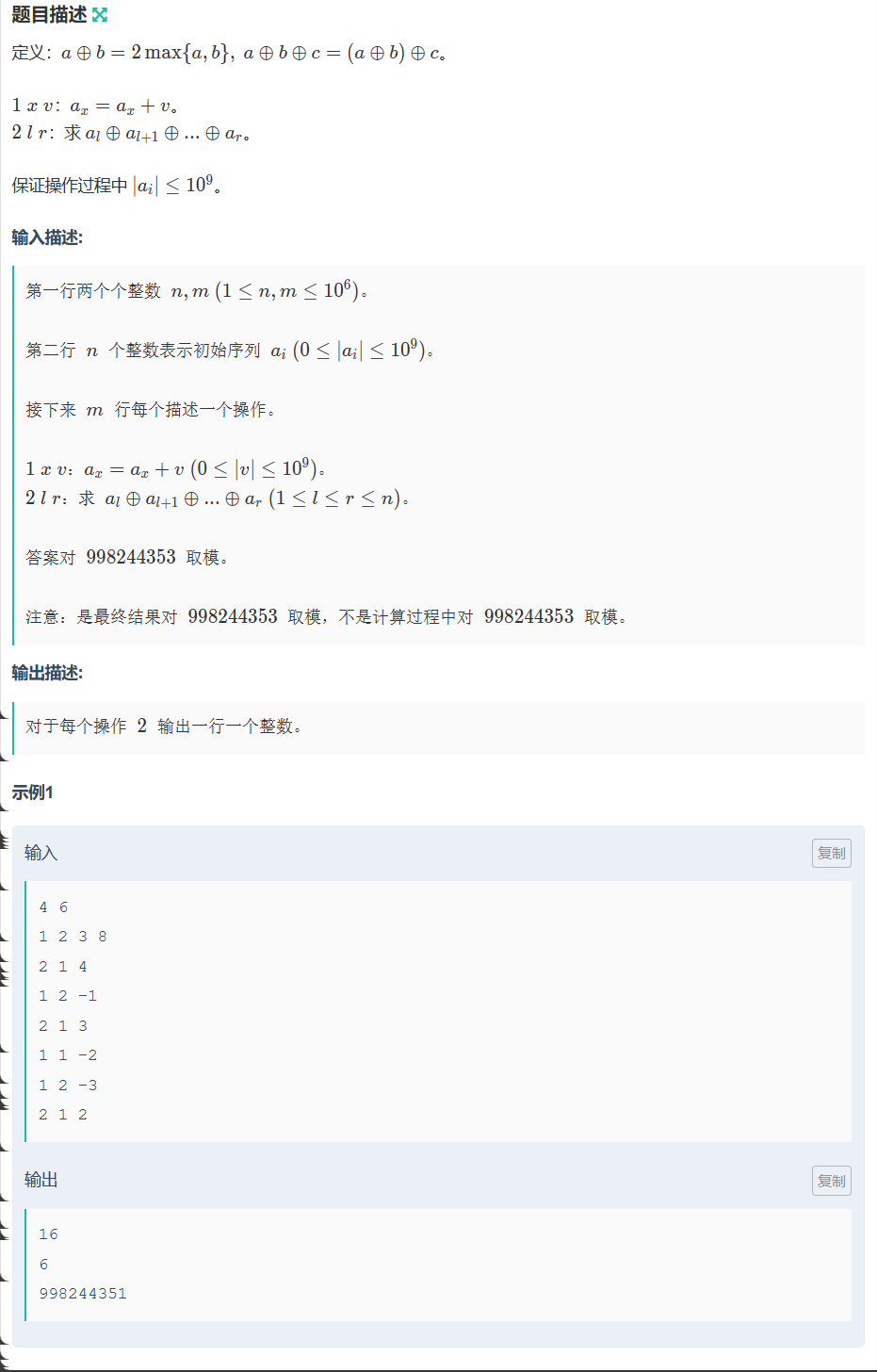
考虑每次操作的特殊性与$a_i$的数据范围，对于一个长度为32的序列，假设经过运算的答案为ans，那么
$$ans=max(2^{30}{a}_l,2^{30}{a}_{l+1},2^{29}{a}_{l+2},2^{28}{a}_{l+3},...,2^1{a}_{r?1},2^0{a}_r)$$
每个$a_i$之前都乘上了一个系数，并且这个系数随着序列长度的增大而增大，当序列长度为32时，前两个数的系数已经达到$2^{30}$。由于$a_i$的最大值为1e9，而$2^{30}>1e9$，所以ans一定大于这个序列之后（$a_r$之后）的数。总结下，若区间[l, r]的前32个数中，存在一个正数，那么ans就是答案
若前32个数中不存在正数，但存在0，那么0就是答案
若前32个数中既不存在正数也不存在0，由于负数乘2会越来越小，所以需要在[l, r]区间的后32数中求ans

实现起来的细节还是很多的：

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int mod9 = 998244353;
const int N = 1e6 + 10;
LL a[N], b[N];
set<int> pos, zr;

LL f(int st, int l, int r)
{
    LL ans = (st == l ? 1 : 2) * a[st];
    int pos = st;
    while (pos + 1 <= r && pos - st <= 30)
        ans = 2 * max(ans, a[++ pos]);
    ans %= mod9;
    ans = ans * b[r - pos] % mod9;
    return (ans % mod9 + mod9) % mod9;
}

void solve()
{
    int n, m; cin >> n >> m; b[0] = 1;
    for (int i = 1; i <= 1000000; ++ i)
        b[i] = b[i - 1] * 2 % mod9;
    for (int i = 1; i <= n; ++ i) 
    {
        cin >> a[i];
        if (a[i] == 0) zr.insert(i);
        else if (a[i] > 0) pos.insert(i);
    }
    while (m --)
    {
        int t; cin >> t;
        if (t == 1)
        {
            int x, v; cin >> x >> v;
            if (a[x] == 0) zr.erase(x);
            else if (a[x] > 0) pos.erase(x);
            a[x] += v;
            if (a[x] == 0) zr.insert(x);
            else if (a[x] > 0) pos.insert(x);
        }
        else
        {
            int l, r; cin >> l >> r;
            auto it = pos.lower_bound(l);
            if (it != pos.end() && *it <= r)
            {
                cout << f(*it, l, r) << "\n";
                continue;
            }
            it = zr.lower_bound(l);
            if (it != zr.end() && *it <= r)
            {
                cout << "0\n";
                continue;
            }
            cout << f(max(l, r - 30), l, r) << "\n";
        }
    }
}

int main()
{
    ios::sync_with_stdio(false), cin.tie(0),cout.tie(0);
    solve();
    return 0;
}