UCB Data100：数据科学的原理和技巧：第六章到第十章

六、正则表达式

原文：Regular Expressions

译者：飞龙

协议：CC BY-NC-SA 4.0

学习成果

• 了解 Python 字符串操作，pandas Series方法

• 解析和创建正则表达式，使用参考表

• 使用词汇（闭包、元字符、组等）描述正则表达式元字符

这些内容在第 6 和第 7 讲中涵盖。

6.1 为什么处理文本？

上一堂课，我们了解了定量和定性变量类型之间的区别。后者包括字符串数据——第 6 讲的主要焦点。在本笔记中，我们将讨论操纵文本所需的工具：python字符串操作和正则表达式。

处理文本有两个主要原因。

1. 规范化：将具有多种格式的数据转换为标准形式。

   • 通过操纵文本，我们可以将具有不匹配字符串标签的表格连接起来。

2. 将信息提取到新特征中。

   • 例如，我们可以从文本中提取日期和时间特征。

6.2 Python 字符串方法

首先，我们将介绍一些有用的字符串操作方法。以下表格包括python和pandas支持的一些字符串操作。python函数操作单个字符串，而它们在pandas中的等效函数是矢量化的——它们操作字符串数据的Series。

操作	Python	Pandas (Series)
转换	s.lower()	ser.str.lower()
	s.upper()	ser.str.upper()
替换 + 删除	s.replace(_)	ser.str.replace(_)
分割	s.split(_)	ser.str.split(_)
子字符串	s[1:4]	ser.str[1:4]
成员资格	'_' in s	ser.str.contains(_)
长度	len(s)	ser.str.len()

我们将在规范化的下一节讨论python字符串函数和pandas Series方法之间的区别。

6.2.1 规范化

假设我们想要合并给定的表格。

代码

import pandas as pd

with open('data/county_and_state.csv') as f:
 county_and_state = pd.read_csv(f)

with open('data/county_and_population.csv') as f:
 county_and_pop = pd.read_csv(f)

display(county_and_state), display(county_and_pop);

	County	State
0	De Witt County	IL
1	Lac qui Parle County	MN
2	Lewis and Clark County	MT
3	St John the Baptist Parish	LS

	County	Population
0	De Witt County	16798
1	Lac qui Parle County	8067
2	Lewis and Clark County	55716
3	St John the Baptist Parish	43044

上次，我们使用主键和外键来连接两个表格。虽然这两个键都不存在于我们的DataFrame中，但是"County"列看起来足够相似。我们能否将这些列转换为一个标准的规范形式，以便合并这两个表格？

6.2.1.1 使用python字符串操作进行规范化

以下函数使用python字符串操作将单个县名转换为规范形式。它通过消除空格、标点和不必要的文本来实现这一点。

def canonicalize_county(county_name):
 return (
 county_name
 .lower()
 .replace(' ', '')
 .replace('&', 'and')
 .replace('.', '')
 .replace('county', '')
 .replace('parish', '')
 )

canonicalize_county("St. John the Baptist")

'stjohnthebaptist'

我们将使用pandas map函数将canonicalize_county函数应用于每个DataFrame中的每一行。这样做，我们将在每个DataFrame中创建一个名为clean_county_python的新列，其中包含规范形式。

county_and_pop['clean_county_python'] = county_and_pop['County'].map(canonicalize_county)
county_and_state['clean_county_python'] = county_and_state['County'].map(canonicalize_county)
display(county_and_state), display(county_and_pop);

	County	State	clean_county_python
0	De Witt County	IL	dewitt
1	Lac qui Parle County	MN	lacquiparle
2	Lewis and Clark County	MT	lewisandclark
3	St. John the Baptist	LS	stjohnthebaptist

	County	Population	clean_county_python
0	De Witt County	16798	dewitt
1	Lac qui Parle County	8067	lacquiparle
2	Lewis and Clark County	55716	lewisandclark
3	St. John the Baptist	43044	stjohnthebaptist

6.2.1.2 使用 Pandas Series 方法进行规范化

或者，我们可以使用pandas Series方法来创建这个标准化的列。为此，我们必须在调用任何方法之前调用我们Series对象的.str属性，比如.lower和.replace。注意这些方法名称与它们在内置的 Python 字符串函数中的等效函数名称相匹配。

以这种方式链接多个 Series 方法可以消除使用 map 函数的需要（因为这段代码是矢量化的）。

def canonicalize_county_series(county_series):
 return (
 county_series
 .str.lower()
 .str.replace(' ', '')
 .str.replace('&', 'and')
 .str.replace('.', '')
 .str.replace('county', '')
 .str.replace('parish', '')
 )

county_and_pop['clean_county_pandas'] = canonicalize_county_series(county_and_pop['County'])
county_and_state['clean_county_pandas'] = canonicalize_county_series(county_and_state['County'])
display(county_and_pop), display(county_and_state);

/var/folders/7t/zbwy02ts2m7cn64fvwjqb8xw0000gp/T/ipykernel_88082/2523629438.py:3: FutureWarning:

The default value of regex will change from True to False in a future version. In addition, single character regular expressions will *not* be treated as literal strings when regex=True.

/var/folders/7t/zbwy02ts2m7cn64fvwjqb8xw0000gp/T/ipykernel_88082/2523629438.py:3: FutureWarning:

The default value of regex will change from True to False in a future version. In addition, single character regular expressions will *not* be treated as literal strings when regex=True. 

	County	Population	clean_county_python	clean_county_pandas
0	DeWitt	16798	dewitt	dewitt
1	Lac Qui Parle	8067	lacquiparle	lacquiparle
2	Lewis & Clark	55716	lewisandclark	lewisandclark
3	St. John the Baptist	43044	stjohnthebaptist	stjohnthebaptist

	County	State	clean_county_python	clean_county_pandas
0	De Witt County	IL	dewitt	dewitt
1	Lac qui Parle County	MN	lacquiparle	lacquiparle
2	Lewis and Clark County	MT	lewisandclark	lewisandclark
3	St John the Baptist Parish	LS	stjohnthebaptist	stjohnthebaptist

6.2.2 提取

提取探讨了从文本数据中获取有用信息的想法。这在模型构建中将特别重要，我们将在几周内学习这个问题。

假设我们想要从一个 .txt 文件中读取一些数据。

with open('data/log.txt', 'r') as f:
 log_lines = f.readlines()

log_lines

['169.237.46.168 - - [26/Jan/2014:10:47:58 -0800] "GET /stat141/Winter04/ HTTP/1.1" 200 2585 "http://anson.ucdavis.edu/courses/"\n',
 '193.205.203.3 - - [2/Feb/2005:17:23:6 -0800] "GET /stat141/Notes/dim.html HTTP/1.0" 404 302 "http://eeyore.ucdavis.edu/stat141/Notes/session.html"\n',
 '169.237.46.240 - "" [3/Feb/2006:10:18:37 -0800] "GET /stat141/homework/Solutions/hw1Sol.pdf HTTP/1.1"\n']

假设我们想要提取日、月、年、小时、分钟、秒和时区。不幸的是，这些项目不是从字符串的开头固定位置开始的，所以通过一些固定偏移量进行切片是行不通的。

相反，我们可以进行一些巧妙的思考。注意到相关信息包含在一组方括号中，进一步由 / 和 : 分隔。我们可以聚焦在文本的这个区域，并在这些字符上分割数据。Python 的内置 .split 函数使这变得容易。

first = log_lines[0] # Only considering the first row of data

pertinent = first.split("[")[1].split(']')[0]
day, month, rest = pertinent.split('/')
year, hour, minute, rest = rest.split(':')
seconds, time_zone = rest.split(' ')
day, month, year, hour, minute, seconds, time_zone

('26', 'Jan', '2014', '10', '47', '58', '-0800')

这段代码有两个问题：

1. Python 的内置函数限制我们一次只能提取一条记录的数据，

   • 这可以使用 map 函数或 pandas Series 方法来解决。

2. 这段代码相当冗长。

   • 这是一个更大的问题，更难解决

在下一节中，我们将介绍正则表达式 - 一种解决问题 2 的工具。

6.3 正则表达式基础知识

**正则表达式（“RegEx”）**是一个指定搜索模式的字符序列。它们被编写用来从文本中提取特定信息。正则表达式本质上是 python 中嵌入的一种较小的编程语言，通过 re 模块提供。因此，它们有独立的语法和各种功能的方法。

正则表达式在数据科学之外的许多应用中都很有用。例如，社会安全号码（SSN）经常使用正则表达式进行验证。

r"[0-9]{3}-[0-9]{2}-[0-9]{4}" # Regular Expression Syntax

# 3 of any digit, then a dash,
# then 2 of any digit, then a dash,
# then 4 of any digit

'[0-9]{3}-[0-9]{2}-[0-9]{4}'

有很多资源可以学习和实验正则表达式。以下是一些资源：

• 官方正则表达式指南

• Data 100 参考资料

• Regex101.com

  • 确保在左侧的类别下选择 Python。

6.3.1 基础正则表达式语法

正则表达式有四种基本操作。

操作	顺序	语法示例	匹配	不匹配
或：|	4	AA|BAAB	AA BAAB	任何其他字符串
连接	3	AABAAB	AABAAB	任何其他字符串
闭包：*（零个或多个）	2	AB*A	AA ABBBBBBA	AB ABABA
分组：()（括号）	1	A(A|B)AAB	AAAAB ABAAB	任何其他字符串
		(AB)*A	A ABABABABA	AA ABBA

注意这些元字符操作的顺序。这些元字符不是字面字符，而是操作相邻字符。() 优先级最高，然后是 *，最后是 |。这使我们能够区分非常不同的正则表达式命令，比如 AB* 和 (AB)*。前者读作“A 然后零个或多个 B”，而后者指定“零个或多个 AB”。

6.3.1.1 示例

问题 1：给出一个匹配 moon、moooon 等的正则表达式。你的表达式应该匹配任何偶数个 o，但不包括零个（即不匹配 mn）。

答案 1：moo(oo)*n

• 在捕获组之前硬编码oo可以确保不匹配mn。

• (oo)*的捕获组确保o的数量是偶数。

问题 2：只使用基本操作，制定一个正则表达式，匹配muun，muuuun，moon，moooon等。你的表达式应该匹配任何偶数个u或o，但不包括零（即不匹配mn）。

答案 2：m(uu(uu)*|oo(oo)*)n

• 以m开头和n结尾确保只匹配以m开头和以n结尾的字符串。

• 注意外部捕获组围绕着|。

  • 考虑正则表达式m(uu(uu)*)|(oo(oo)*)n。这错误地匹配了muu和oooon。

    • 每个 OR 子句是|左右两侧的所有内容。不正确的解决方案只匹配字符串的一半，并且忽略了m开头或n结尾。

    • 必须在|周围加上括号。这样，每个 OR 子句都是|组内左右两侧的所有内容。这确保了m开头和n结尾都被匹配。

6.4 正则表达式扩展

以下提供了更复杂的正则表达式函数。

操作	语法示例	匹配	不匹配
任意字符：.（除换行符外）	.U.U.U.	CUMULUS JUGULUM	SUCCUBUS TUMULTUOUS
字符类：[]（匹配[]中的一个字符）	[A-Za-z][a-z]*	单词首字母大写	驼峰命名 4illegal
重复"a"次：{a}	j[aeiou]{3}hn	jaoehn jooohn	jhn jaeiouhn
重复"a 到 b"次：{a, b}	j[0u]{1,2}hn	john juohn	jhn jooohn
至少一个：+	jo+hn	john joooooohn	jhn jjohn
零或一次：?	joh?n	jon john	任何其他字符串

字符类匹配其类中的单个字符。这些字符可以是硬编码的 - 在[aeiou]的情况下 - 或者可以指定简写以表示一系列字符。例如：

1. [A-Z]：任何大写字母

2. [a-z]：任何小写字母

3. [0-9]：任何单个数字

4. [A-Za-z]：任何大写或小写字母

5. [A-Za-z0-9]：任何大写或小写字母或单个数字

6.4.0.1 示例

让我们分析一些复杂正则表达式的例子。

匹配	不匹配
.*SPB.*
RASPBERRY SPBOO	SUBSPACE SUBSPECIES
[0-9]{3}-[0-9]{2}-[0-9]{4}
231-41-5121 573-57-1821	231415121 57-3571821
[a-z]+@([a-z]+\.)+(edu|com)
horse@pizza.com horse@pizza.food.com	frank_99@yahoo.com hug@cs

解释

1. .*SPB.*只匹配包含子字符串SPB的字符串。

   • .*元字符匹配任意数量的非负字符。换行符不计入其中。

2. 这个正则表达式匹配任意 3 个数字，然后是一个破折号，然后是任意 2 个数字，然后是一个破折号，然后是任意 4 个数字。

   • 你会认出这是熟悉的社会安全号码正则表达式。

3. 匹配任何带有com或edu域的电子邮件，其中电子邮件的所有字符都是字母。

   • 域名前必须至少有一个.。在任何元字符（在本例中是.）之前包括一个反斜杠\告诉正则表达式精确匹配该字符。

6.5 方便的正则表达式

以下是一些更方便的正则表达式。

操作	语法示例	匹配	不匹配
内置字符类	\w+	Fawef_03	this person
	\d+	231123	423 people
	\s+	空白	非空白
字符类否定：[^]（除了给定的字符之外的所有内容）	[^a-z]+.	PEPPERS3982 17211!↑?	porch CLAmS
转义字符：\（匹配下一个字符的字面意义）	cow\.com	cow.com	cowscom
行首：^	^ark	ark two ark o ark	dark
行尾：$	ark$	dark ark o ark	ark two
零或更多的懒惰版本：*?	5.*?5	5005 55	5005005

6.5.1 贪婪性

为了充分理解表中的最后一个操作，我们必须讨论贪婪性。RegEx 是贪婪的 - 它会在字符串中寻找最长可能的匹配。为了举例说明这一点，考虑模式<div>.*</div>。给定下面的句子，我们希望粗体部分会被匹配：

“这是一个正则表达式<div>中</div>的贪婪性的<div>示例</div>。”

实际上，RegEx 处理给定模式的文本的方式如下：

1. “寻找确切的字符串<div>”

2. 然后，“寻找任何字符 0 次或更多次”

3. 然后，“寻找确切的字符串</div>”

结果将是从最左边的<div>到最右边的</div>（包括在内）的所有字符。我们可以通过使我们的模式非贪婪来修复这个问题，<div>.*?</div>。您可以在文档中阅读更多信息这里。

6.5.2 示例

让我们重新审视一下从给定的.txt文件中提取日期/时间数据的早期问题。数据看起来是这样的。

log_lines[0]

'169.237.46.168 - - [26/Jan/2014:10:47:58 -0800] "GET /stat141/Winter04/ HTTP/1.1" 200 2585 "http://anson.ucdavis.edu/courses/"\n'

问题：给出一个正则表达式，匹配括号内和包括括号在内的所有内容 - 天，月，年，小时，分钟，秒和时区。

答案：$$.*$$

• 注意匹配字面上的[和]是必要的。因此，在[和]之前都需要转义字符\ — 否则这些元字符将匹配字符类。

• 我们需要匹配[和]之间的特定格式。对于这个例子，.*就足够了。

备选方案：$$\w+/\w+/\w+:\w+:\w+:\w+\s-\w+$$

• 这个解决方案更安全。

  • 想象一下在[和]之间的数据是垃圾 - .*仍然会匹配它。

  • 备选方案只会匹配符合正确格式的数据。

Python 和 Pandas 中的正则表达式（RegEx 组）

6.6.1 规范化

6.6.1.1 使用正则表达式进行规范化

在本笔记的早期，我们使用python字符串操作和pandas的Series方法来检查规范化的过程。然而，我们提到这种方法有一个主要缺陷：我们的代码过于冗长。有了我们对正则表达式的知识，让我们来修复这个问题。

为此，我们需要了解re模块中的一些函数。其中之一是替换函数：re.sub(pattern, rep1, text)。它的行为类似于python内置的.replace函数，并返回所有pattern的实例被rep1替换后的文本。

这里的正则表达式删除了被<>（也称为 HTML 标签）包围的文本。

按顺序，模式匹配… 1. 单个< 2. 任何不是>的字符：div，td valign…，/td，/div 3. 单个>

在text中的任何子字符串，只要满足所有三个条件，都将被替换为''。

import re

text = "<div><td valign='top'>Moo</td></div>"
pattern = r"<[^>]+>"
re.sub(pattern, '', text) 

'Moo'

注意在正则表达式模式之前的r；这指定了正则表达式是原始字符串。原始字符串不识别转义序列（即 Python 换行元字符\n）。这使它们对于正则表达式非常有用，因为正则表达式通常包含字面上的\字符。

换句话说，不要忘记用r标记你的 RegEx。

6.6.1.2 使用pandas进行规范化

我们还可以使用pandas的Series方法进行正则表达式。这使我们能够操作整列数据，而不是单个值。代码很简单：

ser.str.replace(pattern, repl, regex=True).

考虑以下带有单列的DataFrame html_data。

代码

data = {"HTML": ["<div><td valign='top'>Moo</td></div>", \
 "<a href='http://ds100.org'>Link</a>", \
 "<b>Bold text</b>"]}
html_data = pd.DataFrame(data)

html_data

	HTML
0	<div><td valign='top'>Moo</td></div>
1	<a href='http://ds100.org'>Link</a>
2	<b>Bold text</b>

pattern = r"<[^>]+>"
html_data['HTML'].str.replace(pattern, '', regex=True)

0          Moo
1         Link
2    Bold text
Name: HTML, dtype: object

6.6.2 提取

6.6.2.1 使用正则表达式进行提取

就像规范化一样，re模块提供了从字符串中提取相关文本的功能：

re.findall(pattern, text)。此函数返回与pattern匹配的所有实例的列表。

使用熟悉的社会安全号码的正则表达式：

text = "My social security number is 123-45-6789 bro, or maybe it’s 321-45-6789."
pattern = r"[0-9]{3}-[0-9]{2}-[0-9]{4}"
re.findall(pattern, text) 

['123-45-6789', '321-45-6789']

6.6.2.2 使用pandas进行提取

pandas类似地在数据Series上提供提取功能：ser.str.findall(pattern)

考虑以下DataFrame ssn_data。

代码

data = {"SSN": ["987-65-4321", "forty", \
 "123-45-6789 bro or 321-45-6789",
 "999-99-9999"]}
ssn_data = pd.DataFrame(data)

ssn_data

	SSN
0	987-65-4321
1	forty
2	123-45-6789 bro or 321-45-6789
3	999-99-9999

ssn_data["SSN"].str.findall(pattern)

0                 [987-65-4321]
1                            []
2    [123-45-6789, 321-45-6789]
3                 [999-99-9999]
Name: SSN, dtype: object

该函数返回一个列表，其中包含给定字符串中模式匹配的每一行。

正如你所期望的，pandas还为其他re函数提供了类似的等效功能。Series.str.extract接受一个模式，并返回字符串中每个捕获组的第一个匹配的DataFrame。相比之下，Series.str.extractall返回每个捕获组的所有匹配的多索引DataFrame。你可以在下面的输出中看到差异：

pattern_cg = r"([0-9]{3})-([0-9]{2})-([0-9]{4})"
ssn_data["SSN"].str.extract(pattern_cg)

	0	1	2
0	987	65	4321
1	NaN	NaN	NaN
2	123	45	6789
3	999	99	9999

ssn_data["SSN"].str.extractall(pattern_cg)

		0	1	2
	match
0	0	987	65	4321
2	0	123	45	6789
1	321	45	6789
3	0	999	99	9999

6.6.3 正则表达式捕获组

早些时候，我们使用括号（ ）来指定正则表达式中操作的最高顺序。然而，它们还有另一层含义；括号经常用来表示捕获组。捕获组本质上是一组较小的正则表达式，用于匹配文本数据中的多个子字符串。

让我们看一个例子。

6.6.3.1 示例 1

text = "Observations: 03:04:53 - Horse awakens. \
 03:05:14 - Horse goes back to sleep."

假设我们想要捕获时间数据（小时，分钟和秒）的所有出现作为单独的实体。

pattern_1 = r"(\d\d):(\d\d):(\d\d)"
re.findall(pattern_1, text)

[('03', '04', '53'), ('03', '05', '14')]

注意给定的模式有 3 个捕获组，每个都由正则表达式(\d\d)指定。然后我们使用re.findall返回这些捕获组，每个都包含 3 个匹配的元组。

这些正则表达式捕获组可以是不同的。我们可以使用(\d{2})的速记法来提取相同的数据。

pattern_2 = r"(\d\d):(\d\d):(\d{2})"
re.findall(pattern_2, text)

[('03', '04', '53'), ('03', '05', '14')]

6.6.3.2 示例 2

有了捕获组的概念，让自己相信以下正则表达式是如何工作的。

first = log_lines[0]
first

'169.237.46.168 - - [26/Jan/2014:10:47:58 -0800] "GET /stat141/Winter04/ HTTP/1.1" 200 2585 "http://anson.ucdavis.edu/courses/"\n'

pattern = r'$$(\d+)\/(\w+)\/(\d+):(\d+):(\d+):(\d+) (.+)$$'
day, month, year, hour, minute, second, time_zone = re.findall(pattern, first)[0]
print(day, month, year, hour, minute, second, time_zone)

26 Jan 2014 10 47 58 -0800

6.7 正则表达式的局限性

今天，我们探讨了在数据整理中使用正则表达式处理文本数据的能力。然而，还有一些需要注意的事项。

编写正则表达式就像编写程序一样。

• 需要熟悉语法。

• 写起来可能比读起来更容易。

• 可能很难调试。

正则表达式在某些类型的问题上表现糟糕：

• 对于解析分层结构，比如 JSON，使用json.load()解析器，而不是 RegEx！

• 复杂特性（例如有效的电子邮件地址）。

• 计数（a 和 b 的实例数相同）。 （不可能）

• 复杂属性（回文，平衡括号）。 （不可能）

最终的目标不是记住所有的正则表达式。相反，目标是：

• 了解 RegEx 的能力。

• 解析和创建 RegEx，使用参考表

• 使用词汇（元字符，转义字符，组等）描述正则表达式元字符。

• 区分()，[]，{}

• 设计自己的字符类，使用，，[…-…]，^等。

• 使用python和pandas的 RegEx 方法。

七、可视化 I

原文：Visualization I

译者：飞龙

协议：CC BY-NC-SA 4.0

学习成果

• 使用matplotlib和seaborn创建数据可视化。

• 分析直方图，识别偏斜、潜在异常值和众数。

• 使用boxplot和violinplot比较两个分布。

这个内容在第 7 讲中涵盖。

在我们的数据科学生命周期中，我们已经开始探索广阔的探索性数据分析世界。最近，我们学会了使用各种数据处理技术对数据进行预处理。当我们努力理解我们的数据时，我们的工具中缺少一个关键组件——即可视化和识别现有数据中的关系的能力。

接下来的两节课将向您介绍各种数据可视化的例子及其基本理论。通过这样做，我们将以绘图库的使用在真实世界的例子中激发它们的重要性。

7.1 Data 8 和 Data 100 中的可视化（到目前为止）

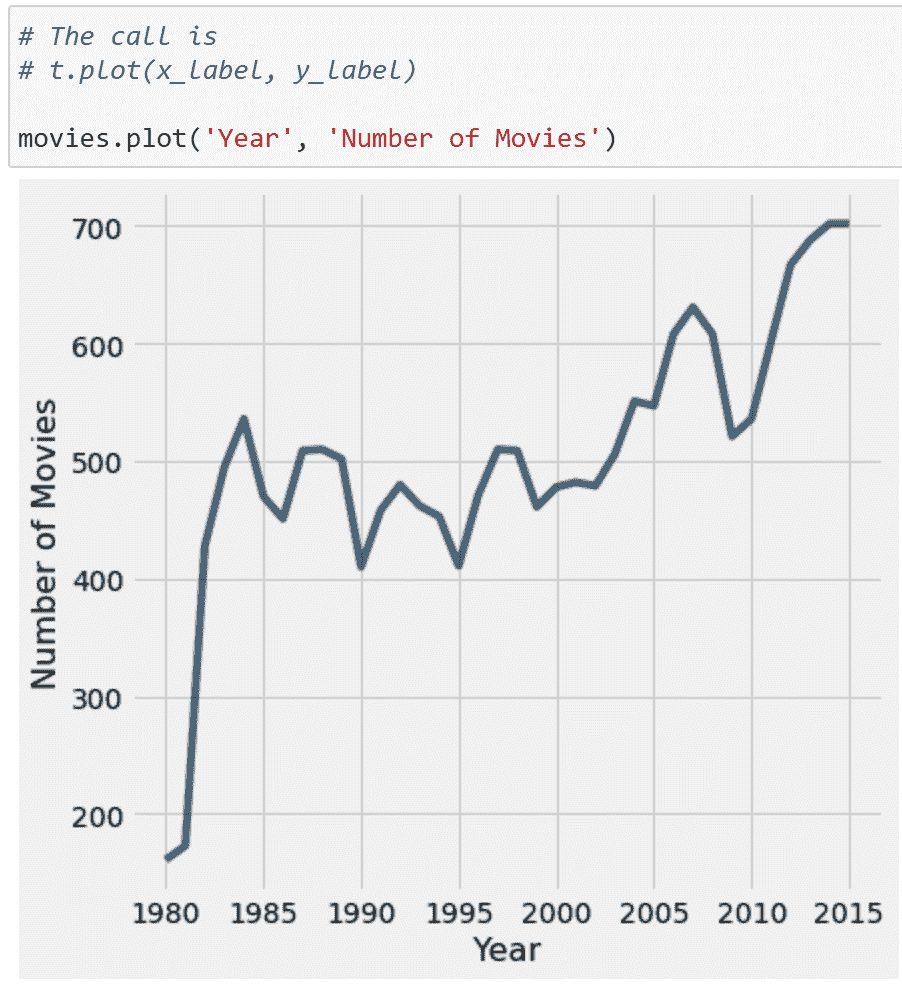
在学习过程中，您可能遇到了几种形式的数据可视化。您可能还记得 Data 8 中的两个例子：折线图和直方图。每个都有独特的用途。例如，折线图显示了数值数量随时间的变化，而直方图有助于理解变量的分布。

折线图

直方图

7.2 可视化的目标

可视化有许多用途。在 Data 100 中，我们特别考虑了两个领域：

1. 为了扩大您对数据的理解

   • 探索性数据分析中的关键部分。

   • 有助于调查变量之间的关系。

2. 向他人传达结果/结论

   • 可视化理论在这里尤为重要。

可视化最常见的应用之一是理解数据的分布。

本课程笔记将重点介绍 Data 100 中可视化主题的前半部分。这里的目标是了解如何根据不同的变量类型选择“正确”的图表，其次是如何使用代码生成这些图表。

7.3 分布概述

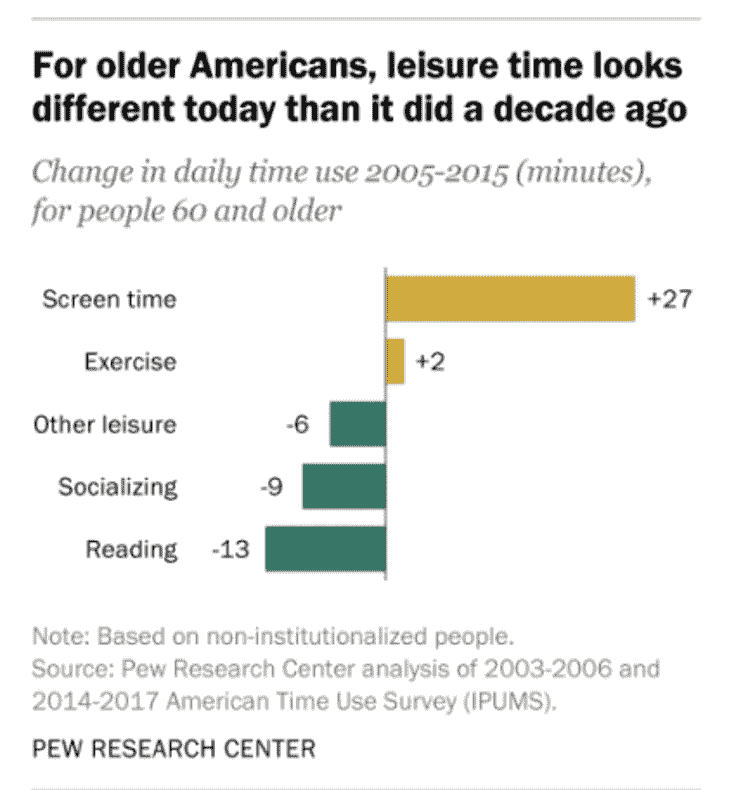
分布描述了变量中唯一值的频率。分布必须满足两个属性：

1. 每个数据点必须属于一个类别。

2. 所有类别的总频率必须相加等于 100%。换句话说，它们的总计数应等于考虑的值的数量。

无效的分布

有效的分布

左图：这不是一个有效的分布，因为个体可以与多个类别相关联，条形值表示的是分钟而不是概率。

右图：这个例子满足了分布的两个属性，因此它是一个有效的分布。

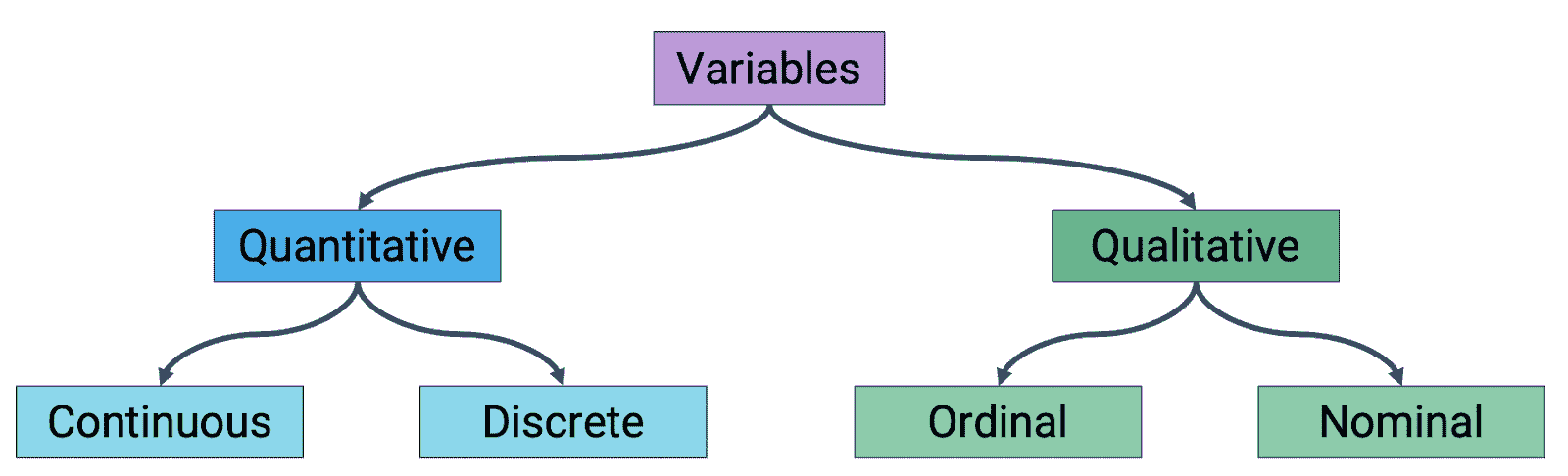
7.4 变量类型应指导绘图选择

不同的图表更或者更不适合显示特定类型的变量，如下图所示：

7.5 条形图

正如我们上面看到的，条形图是显示定性（分类）变量分布的最常见方式之一。条形图的长度编码了类别的频率；宽度没有编码有用的信息。颜色可能表示一个子类别，但这并不一定是这样。

让我们通过一个例子来加以说明。我们将在分析中使用世界银行数据集（wb）。

代码

import pandas as pd
import numpy as np

wb = pd.read_csv("data/world_bank.csv", index_col=0)
wb.head()

	Continent	Country	Primary completion rate: Male: % of relevant age group: 2015	Primary completion rate: Female: % of relevant age group: 2015	Lower secondary completion rate: Male: % of relevant age group: 2015	Lower secondary completion rate: Female: % of relevant age group: 2015	Youth literacy rate: Male: % of ages 15-24: 2005-14	Youth literacy rate: Female: % of ages 15-24: 2005-14	Adult literacy rate: Male: % ages 15 and older: 2005-14	Adult literacy rate: Female: % ages 15 and older: 2005-14	…	Access to improved sanitation facilities: % of population: 1990	Access to improved sanitation facilities: % of population: 2015	Child immunization rate: Measles: % of children ages 12-23 months: 2015	Child immunization rate: DTP3: % of children ages 12-23 months: 2015	Children with acute respiratory infection taken to health provider: % of children under age 5 with ARI: 2009-2016	Children with diarrhea who received oral rehydration and continuous feeding: % of children under age 5 with diarrhea: 2009-2016	Children sleeping under treated bed nets: % of children under age 5: 2009-2016	Children with fever receiving antimalarial drugs: % of children under age 5 with fever: 2009-2016	Tuberculosis: Treatment success rate: % of new cases: 2014	Tuberculosis: Cases detection rate: % of new estimated cases: 2015
0	Africa	Algeria	106.0	105.0	68.0	85.0	96.0	92.0	83.0	68.0	…	80.0	88.0	95.0	95.0	66.0	42.0	NaN	NaN	88.0	80.0
1	Africa	Angola	NaN	NaN	NaN	NaN	79.0	67.0	82.0	60.0	…	22.0	52.0	55.0	64.0	NaN	NaN	25.9	28.3	34.0	64.0
2	Africa	Benin	83.0	73.0	50.0	37.0	55.0	31.0	41.0	18.0	…	7.0	20.0	75.0	79.0	23.0	33.0	72.7	25.9	89.0	61.0
3	Africa	Botswana	98.0	101.0	86.0	87.0	96.0	99.0	87.0	89.0	…	39.0	63.0	97.0	95.0	NaN	NaN	NaN	NaN	77.0	62.0
5	Africa	Burundi	58.0	66.0	35.0	30.0	90.0	88.0	89.0	85.0	…	42.0	48.0	93.0	94.0	55.0	43.0	53.8	25.4	91.0	51.0

5 行 × 47 列

我们可以使用条形图来可视化 Continent 列的分布。有几种方法可以做到这一点。

7.5.1 在 Pandas 中绘图

wb['Continent'].value_counts().plot(kind = 'bar');

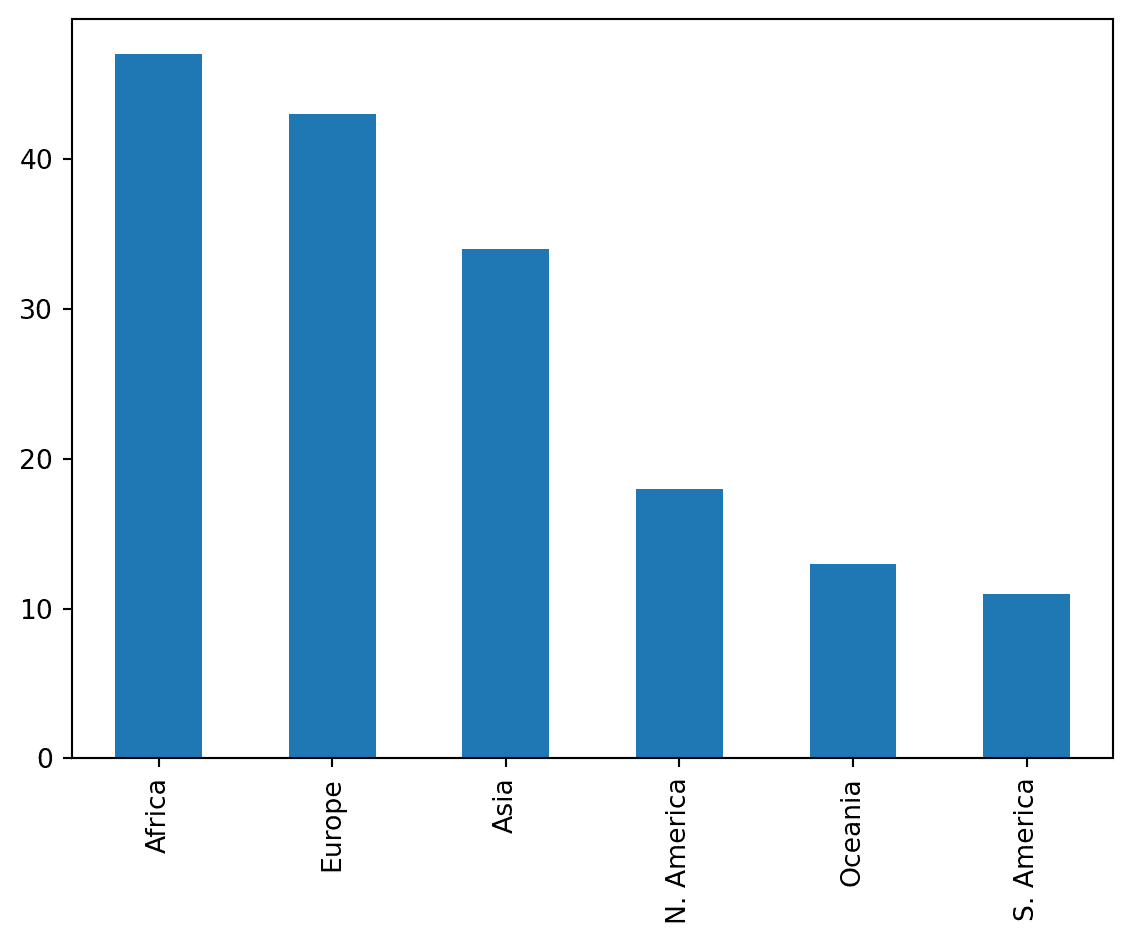
回想一下，.value_counts() 返回一个 Series，其中包含每个唯一值的总计数。我们在这个结果上调用 .plot(kind = 'bar') 来将这些计数可视化为条形图。

pandas 中的绘图方法是最不受欢迎的，也不受 Data 100 的支持，因为它们的功能有限。相反，未来的示例将专注于其他专门用于可视化数据的库。这里最知名的库是 matplotlib。

7.5.2 在 Matplotlib 中绘图

import matplotlib.pyplot as plt # matplotlib is typically given the alias plt

continent = wb['Continent'].value_counts()
plt.bar(continent.index, continent)
plt.xlabel('Continent')
plt.ylabel('Count');

虽然需要更多的代码来实现相同的结果，但 matplotlib 通常比 pandas 更常用，因为它能够绘制更复杂的可视化效果，其中一些很快就会讨论。

然而，请注意我们需要使用 plt.xlabel 和 plt.ylabel 标记轴 - matplotlib 不支持自动轴标记。为了避免这些不便，我们可以使用更高效的绘图库 seaborn。

7.5.3 在 Seaborn 中绘图

import seaborn as sns # seaborn is typically given the alias sns
sns.countplot(data = wb, x = 'Continent');

seaborn.countplot 既计算又可视化给定列中唯一值的数量。这一列由 x 参数指定为 sns.countplot，而 DataFrame 由 data 参数指定。与 matplotlib 相反，seaborn 调用的一般结构涉及传入整个 DataFrame，然后指定要绘制的列。

对于绝大多数可视化，seaborn比matplotlib更简洁和美观。然而，这个特定条形图的颜色方案是任意的 - 它并不额外编码有关类别本身的任何信息。这并不总是正确的；颜色可能在其他可视化中表示有意义的细节。我们将在下一讲中更深入地探讨这一点。

到目前为止，您可能已经注意到这些绘图库的语法各不相同。与pandas一样，我们将教您matplotlib和seaborn中的重要方法，但您将通过文档学到更多。

1. Matplotlib 文档

2. Seaborn 文档

回想我们的第二个目标，当我们想要使用可视化来向他人传达结果/结论时，我们必须考虑：

• 我们应该使用什么颜色？

• 条的宽度应该是多少？

• 图例是否存在？

• 条形和坐标轴应该有深色边框吗？

为了实现这一点，以下是我们可以改进绘图的一些方法：

• 为每个条引入不同的颜色

• 包括图例

• 包括标题

• 标记 y 轴

• 使用色盲友好的调色板

• 重新定位标签

• 增加字体大小

7.6 定量变量的分布

重新审视我们的wb DataFrame 的示例，让我们绘制人均国民总收入的分布。

代码

wb.head(5)

	Continent	Country	Primary completion rate: Male: % of relevant age group: 2015	Primary completion rate: Female: % of relevant age group: 2015	Lower secondary completion rate: Male: % of relevant age group: 2015	Lower secondary completion rate: Female: % of relevant age group: 2015	Youth literacy rate: Male: % of ages 15-24: 2005-14	Youth literacy rate: Female: % of ages 15-24: 2005-14	Adult literacy rate: Male: % ages 15 and older: 2005-14	Adult literacy rate: Female: % ages 15 and older: 2005-14	…	Access to improved sanitation facilities: % of population: 1990	Access to improved sanitation facilities: % of population: 2015	Child immunization rate: Measles: % of children ages 12-23 months: 2015	Child immunization rate: DTP3: % of children ages 12-23 months: 2015	Children with acute respiratory infection taken to health provider: % of children under age 5 with ARI: 2009-2016	Children with diarrhea who received oral rehydration and continuous feeding: % of children under age 5 with diarrhea: 2009-2016	Children sleeping under treated bed nets: % of children under age 5: 2009-2016	Children with fever receiving antimalarial drugs: % of children under age 5 with fever: 2009-2016	Tuberculosis: Treatment success rate: % of new cases: 2014	Tuberculosis: Cases detection rate: % of new estimated cases: 2015
0	Africa	Algeria	106.0	105.0	68.0	85.0	96.0	92.0	83.0	68.0	…	80.0	88.0	95.0	95.0	66.0	42.0	NaN	NaN	88.0	80.0
1	Africa	Angola	NaN	NaN	NaN	NaN	79.0	67.0	82.0	60.0	…	22.0	52.0	55.0	64.0	NaN	NaN	25.9	28.3	34.0	64.0
2	Africa	Benin	83.0	73.0	50.0	37.0	55.0	31.0	41.0	18.0	…	7.0	20.0	75.0	79.0	23.0	33.0	72.7	25.9	89.0	61.0
3	Africa	Botswana	98.0	101.0	86.0	87.0	96.0	99.0	87.0	89.0	…	39.0	63.0	97.0	95.0	NaN	NaN	NaN	NaN	77.0	62.0
5	Africa	Burundi	58.0	66.0	35.0	30.0	90.0	88.0	89.0	85.0	…	42.0	48.0	93.0	94.0	55.0	43.0	53.8	25.4	91.0	51.0

5 行×47 列

我们应该如何定义这个变量的类别？在前面的例子中，这些是Continent列的几个唯一值。如果我们在这里使用类似的逻辑，我们的类别就是人均国民总收入列中包含的不同数值。

在这个假设下，让我们使用seaborn.countplot函数绘制这个分布。

sns.countplot(data = wb, x = 'Gross national income per capita, Atlas method: $: 2016');

发生了什么？条形图（plt.bar或sns.countplot）将为变量的每个唯一值创建一个单独的条。对于连续变量，我们可能没有有限数量的可能值，这可能导致我们需要许多条来显示每个唯一值的情况。

具体来说，我们可以说这个直方图受到重叠绘图的影响，因为我们无法解释图表并获得任何有意义的见解。

与条形图不同，为了可视化连续变量的分布，我们使用以下类型的图之一：

• 直方图

• 箱线图

• 小提琴图

7.7 箱线图和小提琴图

箱线图和小提琴图是两种非常相似的可视化类型。两者都使用四分位数的信息显示变量的分布。

在箱线图中，箱子在任意点的宽度不编码含义。在小提琴图中，图的宽度表示每个可能值的分布密度。

sns.boxplot(data=wb, y='Gross national income per capita, Atlas method: $: 2016');

sns.violinplot(data=wb, y="Gross national income per capita, Atlas method: $: 2016");

四分位数代表数据的 25%部分。我们说：

• 第一四分位数（Q1）代表第 25 百分位数-25%的数据位于第一四分位数以下。

• 第二四分位数（Q2）代表第 50 百分位数，也称为中位数-50%的数据位于第二四分位数以下。

• 第三四分位数（Q3）代表第 75 百分位数-75%的数据位于第三四分位数以下。

这意味着数据的中间 50%位于第一和第三四分位数之间。这在下面的直方图中得到了证明。三个四分位数用红色垂直线标记。

gdp = wb['Gross domestic product: % growth : 2016']
gdp = gdp[~gdp.isna()]

q1, q2, q3 = np.percentile(gdp, [25, 50, 75])

wb_quartiles = wb.copy()
wb_quartiles['category'] = None
wb_quartiles.loc[(wb_quartiles['Gross domestic product: % growth : 2016'] < q1) | (wb_quartiles['Gross domestic product: % growth : 2016'] > q3), 'category'] = 'Outside of the middle 50%'
wb_quartiles.loc[(wb_quartiles['Gross domestic product: % growth : 2016'] > q1) & (wb_quartiles['Gross domestic product: % growth : 2016'] < q3), 'category'] = 'In the middle 50%'

sns.histplot(wb_quartiles, x="Gross domestic product: % growth : 2016", hue="category")
sns.rugplot([q1, q2, q3], c="firebrick", lw=6, height=0.1);

在箱线图中，箱子的下限位于 Q1，而箱子的上限位于 Q3。箱子中间的水平线对应于 Q2（或者说中位数）。

sns.boxplot(data=wb, y='Gross domestic product: % growth : 2016');

箱线图的须是位于[（1 四分位-（1.5×IQR））]和[（3 四分位+（1.5×IQR））]的两个点。它们是“正常”数据的下限和上限范围（不包括异常值的点）。

箱线图中包含的不同形式的信息可以总结如下：

小提琴图显示四分位数信息，尽管有点微妙。仔细看下面小提琴图的中心垂直条！

sns.violinplot(data=wb, y='Gross domestic product: % growth : 2016');

7.8 并列箱线图和小提琴图

绘制并列的箱线图或小提琴图可以让我们比较不同类别的分布。换句话说，它们使我们能够在一个可视化中绘制定性变量和定量连续变量。

使用seaborn，我们可以通过指定 x 和 y 列轻松创建并列图。

sns.boxplot(data=wb, x="Continent", y='Gross domestic product: % growth : 2016');

7.9 绘制直方图

您可能熟悉 Data 8 中的直方图。直方图将连续数据收集到箱中，然后绘制这些分箱数据。每个箱反映了数值位于箱的左右端之间的数据点的密度。

# The `edgecolor` argument controls the color of the bin edges
gni = wb["Gross national income per capita, Atlas method: $: 2016"]
plt.hist(gni, density=True, edgecolor="white")

# Add labels
plt.xlabel("Gross national income per capita")
plt.ylabel("Density")
plt.title("Distribution of gross national income per capita");

sns.histplot(data=wb, x="Gross national income per capita, Atlas method: $: 2016", stat="density")
plt.title("Distribution of gross national income per capita");

7.9.1 重叠直方图

我们可以叠加直方图（或密度曲线）来比较定性类别的分布。

sns.histplot的hue参数指定应该用于确定每个类别颜色的列。hue可以在许多seaborn绘图函数中使用。

请注意，生成的图表包括一个图例，描述每个半球对应的颜色 - 如果颜色用于编码可视化中的信息，则应始终包括图例！

# Create a new variable to store the hemisphere in which each country is located
north = ["Asia", "Europe", "N. America"]
south = ["Africa", "Oceania", "S. America"]
wb.loc[wb["Continent"].isin(north), "Hemisphere"] = "Northern"
wb.loc[wb["Continent"].isin(south), "Hemisphere"] = "Southern"

sns.histplot(data=wb, x="Gross national income per capita, Atlas method: $: 2016", hue="Hemisphere", stat="density")
plt.title("Distribution of gross national income per capita");

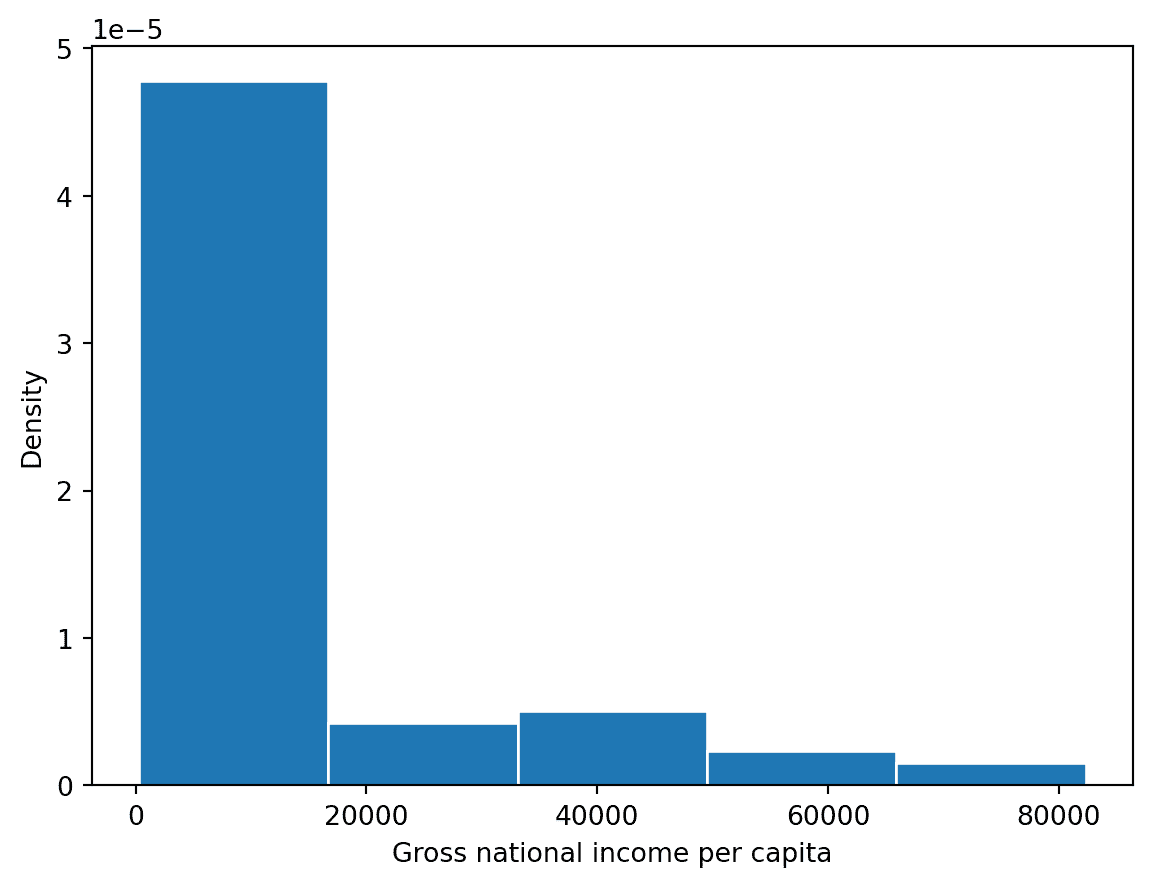
直方图的每个箱子都经过缩放，使其面积等于其包含的所有数据点的百分比。

densities, bins, _ = plt.hist(gni, density=True, edgecolor="white", bins=5)
plt.xlabel("Gross national income per capita")
plt.ylabel("Density")

print(f"First bin has width {bins[1]-bins[0]} and height {densities[0]}")
print(f"This corresponds to {bins[1]-bins[0]} * {densities[0]} = {(bins[1]-bins[0])*densities[0]*100}% of the data")

First bin has width 16410.0 and height 4.7741589911386953e-05
This corresponds to 16410.0 * 4.7741589911386953e-05 = 78.343949044586% of the data

7.10 评估直方图

直方图允许我们通过它们的形状来评估分布。我们可以分析直方图的一些属性：

1. 偏斜和尾部

   • 左偏 vs 右偏

   • 左尾 vs 右尾

2. 异常值

   • 使用百分位数

3. 模式

   • 最常出现的数据

7.10.1 偏斜和尾部

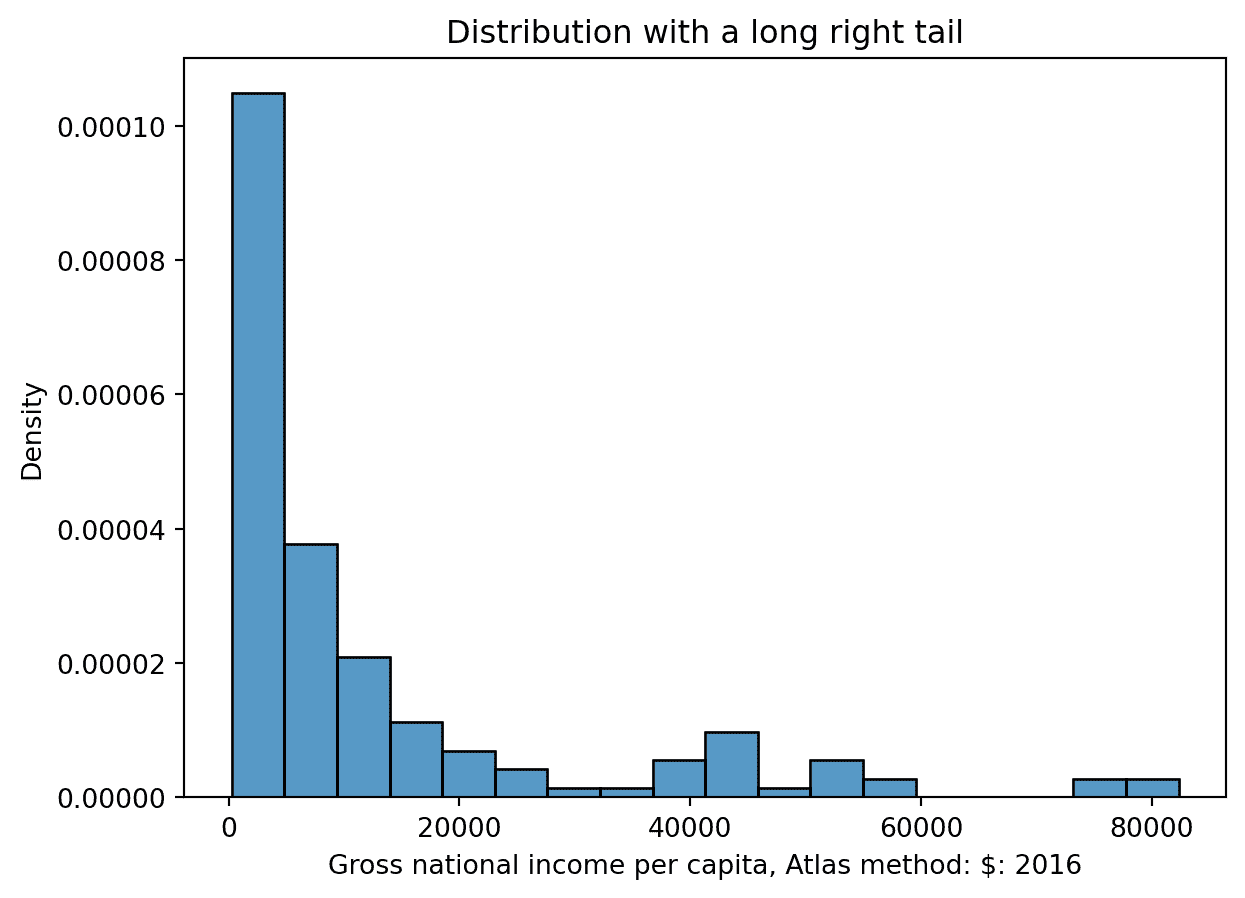
直方图的偏斜描述了其“尾巴”延伸的方向。- 具有较长右尾的分布是右偏的（例如人均国民总收入）。在右偏分布中，少数大的异常值将均值“拉”到中位数的右侧。- 具有较长左尾的分布是左偏的（例如改善的饮水来源）。在左偏分布中，少数小的异常值将均值“拉”到中位数的左侧。

在分布的右尾和左尾大小相等的情况下，它是对称的。均值大约等于中位数。将均值视为分布的平衡点。

sns.histplot(data = wb, x = 'Gross national income per capita, Atlas method: $: 2016', stat = 'density');
plt.title('Distribution with a long right tail')

Text(0.5, 1.0, 'Distribution with a long right tail')

sns.histplot(data = wb, x = 'Access to an improved water source: % of population: 2015', stat = 'density');
plt.title('Distribution with a long left tail')

Text(0.5, 1.0, 'Distribution with a long left tail')

7.10.2 异常值

粗略地说，异常值被定义为与其他值相比距离异常大的数据点。让我们更具体地描述一下。正如您可能在之前的箱线图信息图表中观察到的，我们将异常值定义为超出触须的数据点。具体来说，小于[$第1四分位数?(1.5\times$ IQR)]或大于[$第3四分位数+(1.5\times$ IQR)]的值。

7.10.3 模式

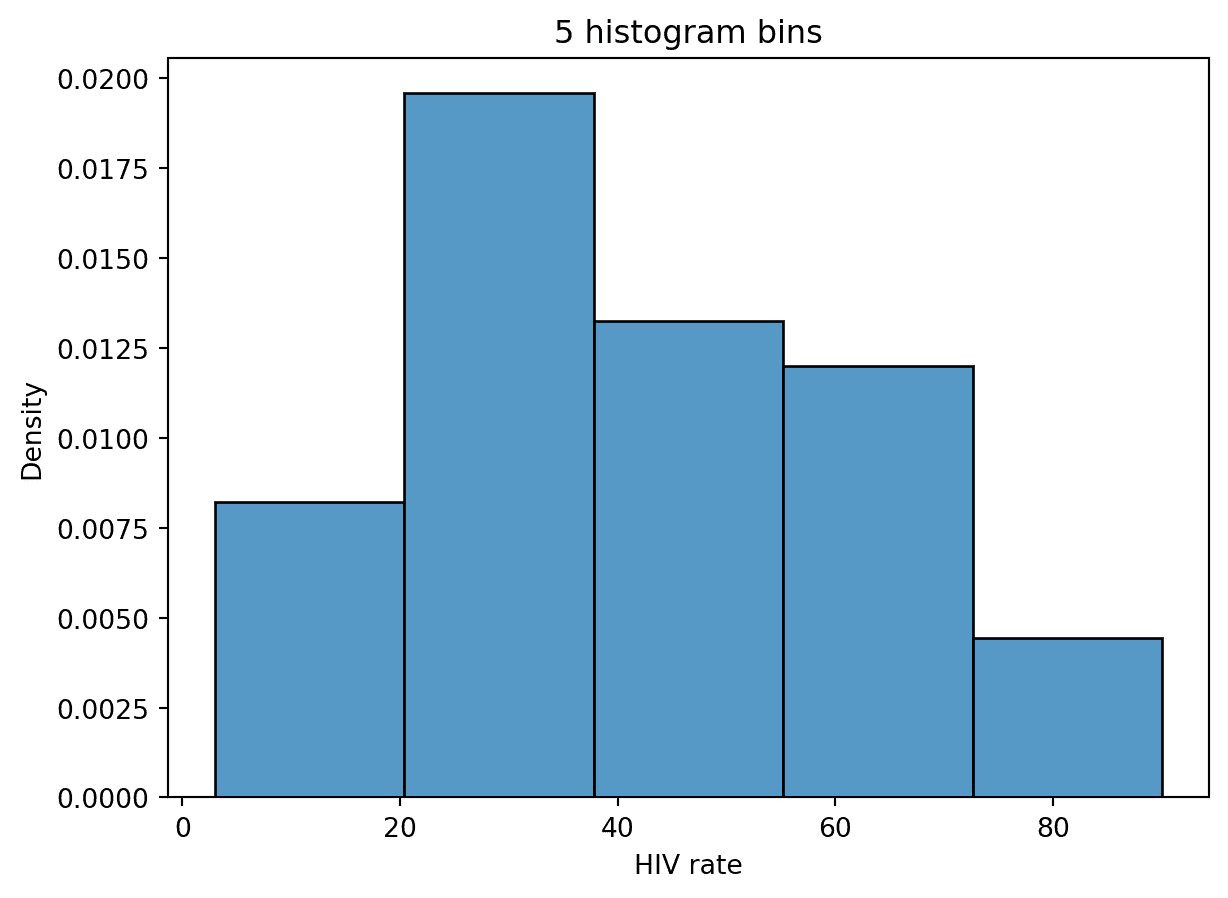
在 Data 100 中，我们将直方图的“模式”描述为分布中的峰值。然而，通常很难确定什么算作自己的“峰值”。例如，HIV 率在不同国家之间的分布的峰值数量取决于我们绘制的直方图箱数。

如果我们将箱数设置为 5，则分布呈单峰分布。

# Rename the very long column name for convenience
wb = wb.rename(columns={'Antiretroviral therapy coverage: % of people living with HIV: 2015':"HIV rate"})
# With 5 bins, it seems that there is only one peak
sns.histplot(data=wb, x="HIV rate", stat="density", bins=5)
plt.title("5 histogram bins");

# With 10 bins, there seem to be two peaks

sns.histplot(data=wb, x="HIV rate", stat="density", bins=10)
plt.title("10 histogram bins");

# And with 20 bins, it becomes hard to say what counts as a "peak"!

sns.histplot(data=wb, x ="HIV rate", stat="density", bins=20)
plt.title("20 histogram bins");

在某种程度上，正是这些模糊性促使我们考虑使用核密度估计（KDE），我们将在下一讲中更多地探讨。

八、可视化 II

原文：Visualization II

译者：飞龙

协议：CC BY-NC-SA 4.0

学习成果

• 了解用于绘制分布和估计密度曲线的 KDE。

• 使用转换分析两个变量之间的关系。

• 根据可视化理论概念评估可视化的质量。

8.0.1 核密度估计

8.0.1.1 KDE 理论

现在让我们深入研究核密度估计。**核密度估计（KDE）**是一种平滑的连续函数，它近似表示一条曲线。它们允许我们表示分布的一般趋势，而不专注于细节，这对于分析数据集的广泛结构是有用的。

更正式地说，KDE 试图近似我们的数据集抽取的潜在概率分布。您可能在其他课程中遇到过概率分布的概念；如果没有，我们将在下一讲中详细讨论。现在，您可以将概率分布视为描述我们在数据集中抽取特定值的可能性有多大。

KDE 曲线估计随机变量的概率密度函数。考虑下面的例子，我们使用sns.displot绘制了直方图（包含我们实际收集的数据点）和 KDE 曲线（代表近似概率分布，从中抽取了这些数据）使用我们之前使用过的世界银行数据集（wb）。

代码

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

wb = pd.read_csv("data/world_bank.csv", index_col=0)
wb = wb.rename(columns={'Antiretroviral therapy coverage: % of people living with HIV: 2015':"HIV rate",
 'Gross national income per capita, Atlas method: $: 2016':'gni'})
wb.head()

	Continent	Country	Primary completion rate: Male: % of relevant age group: 2015	Primary completion rate: Female: % of relevant age group: 2015	Lower secondary completion rate: Male: % of relevant age group: 2015	Lower secondary completion rate: Female: % of relevant age group: 2015	Youth literacy rate: Male: % of ages 15-24: 2005-14	Youth literacy rate: Female: % of ages 15-24: 2005-14	Adult literacy rate: Male: % ages 15 and older: 2005-14	Adult literacy rate: Female: % ages 15 and older: 2005-14	…	Access to improved sanitation facilities: % of population: 1990	Access to improved sanitation facilities: % of population: 2015	Child immunization rate: Measles: % of children ages 12-23 months: 2015	Child immunization rate: DTP3: % of children ages 12-23 months: 2015	Children with acute respiratory infection taken to health provider: % of children under age 5 with ARI: 2009-2016	Children with diarrhea who received oral rehydration and continuous feeding: % of children under age 5 with diarrhea: 2009-2016	Children sleeping under treated bed nets: % of children under age 5: 2009-2016	Children with fever receiving antimalarial drugs: % of children under age 5 with fever: 2009-2016	Tuberculosis: Treatment success rate: % of new cases: 2014	Tuberculosis: Cases detection rate: % of new estimated cases: 2015
0	Africa	Algeria	106.0	105.0	68.0	85.0	96.0	92.0	83.0	68.0	…	80.0	88.0	95.0	95.0	66.0	42.0	NaN	NaN	88.0	80.0
1	Africa	Angola	NaN	NaN	NaN	NaN	79.0	67.0	82.0	60.0	…	22.0	52.0	55.0	64.0	NaN	NaN	25.9	28.3	34.0	64.0
2	Africa	Benin	83.0	73.0	50.0	37.0	55.0	31.0	41.0	18.0	…	7.0	20.0	75.0	79.0	23.0	33.0	72.7	25.9	89.0	61.0
3	Africa	Botswana	98.0	101.0	86.0	87.0	96.0	99.0	87.0	89.0	…	39.0	63.0	97.0	95.0	NaN	NaN	NaN	NaN	77.0	62.0
5	Africa	Burundi	58.0	66.0	35.0	30.0	90.0	88.0	89.0	85.0	…	42.0	48.0	93.0	94.0	55.0	43.0	53.8	25.4	91.0	51.0

5 行×47 列

import seaborn as sns
import matplotlib.pyplot as plt

sns.displot(data = wb, x = 'HIV rate', \
 kde = True, stat = "density")

plt.title("Distribution of HIV rates");

/Users/Ishani/micromamba/lib/python3.9/site-packages/seaborn/axisgrid.py:118: UserWarning:

The figure layout has changed to tight 

注意，平滑的 KDE 曲线在直方图箱更高时更高。你可以将 KDE 曲线的高度看作代表我们随机抽样具有相应值的数据点的“可能性”有多大。这在直观上是有意义的 - 如果我们已经收集了更多具有特定值的数据点（导致一个高的直方图箱），那么如果我们随机抽样另一个数据点，我们更有可能抽样到一个具有类似值的数据点（导致高的 KDE 曲线）。

概率密度函数下的面积应该始终积分为 1，表示分布的总概率应始终总和为 100%。因此，KDE 曲线下始终有一个面积为 1。

8.0.1.2 构建 KDE

我们使用三个步骤进行核密度估计。

1. 在每个数据点放置一个核。

2. 将核函数归一化，使其总面积为 1（跨所有核函数）。

3. 对归一化的核求和。

我们马上会解释“核”是什么。

为了简化，让我们为一个由 5 个数据点构成的小型人工生成的数据集$[2.2,2.8,3.7,5.3,5.7]$构建一个 KDE。在下面的图中，每个垂直条代表一个数据点。

代码

data = [2.2, 2.8, 3.7, 5.3, 5.7]

sns.rugplot(data, height=0.3)

plt.xlabel("Data")
plt.ylabel("Density")
plt.xlim(-3, 10)
plt.ylim(0, 0.5);

我们的目标是创建以下由sns.kdeplot自动生成的 KDE 曲线。

代码

sns.kdeplot(data)

plt.xlabel("Data")
plt.xlim(-3, 10)
plt.ylim(0, 0.5);

8.0.1.2.1 步骤 1：在每个数据点上放置一个核

要开始生成密度曲线，我们需要选择一个核和带宽值（$\alpha$)。这些究竟是什么？

核是一个密度曲线。它是试图捕捉我们采样数据中每个数据点的随机性的数学函数。为了解释这意味着什么，考虑我们数据集中的一个数据点：$2.2$。我们通过随机抽样得到了这个数据点（你可以想象$2.2$代表实验中进行的单次测量，例如）。如果我们抽样一个新的数据点，可能会得到一个略有不同的值。它可能高于$2.2$；也可能低于$2.2$。我们假设任何未来抽样的数据点可能与我们已经绘制的数据值相似。这意味着我们的核 - 我们对随机抽样任何新值的概率的描述 - 在我们已经绘制的数据点处最大，但在其上下仍具有非零概率。任何核下的面积应该积分为 1，表示抽取新数据点的总概率。

带宽值通常用 $\alpha$ 表示，表示核的宽度。 $\alpha$ 的值越大，核函数就会变得宽而短，而值越小，核函数就会变得窄而高。

下面，我们在数据点$2.2$上放置了一个高斯核，用橙色绘制。高斯核简单地是正态分布，在 Data 8 中可能称为钟形曲线。

代码

def gaussian_kernel(x, z, a):
 # We'll discuss where this mathematical formulation came from later
 return (1/np.sqrt(2*np.pi*a**2)) * np.exp((-(x - z)**2 / (2 * a**2)))

# Plot our datapoint
sns.rugplot([2.2], height=0.3)

# Plot the kernel
x = np.linspace(-3, 10, 1000)
plt.plot(x, gaussian_kernel(x, 2.2, 1))

plt.xlabel("Data")
plt.ylabel("Density")
plt.xlim(-3, 10)
plt.ylim(0, 0.5);

要开始创建我们的 KDE，我们在我们的数据集中的每个数据点上放置一个核。对于我们的 5 个数据点的数据集，我们将有 5 个核。

代码

# You will work with the functions below in Lab 4
def create_kde(kernel, pts, a):
 # Takes in a kernel, set of points, and alpha
 # Returns the KDE as a function
 def f(x):
 output = 0
 for pt in pts:
 output += kernel(x, pt, a)
 return output / len(pts) # Normalization factor
 return f

def plot_kde(kernel, pts, a):
 # Calls create_kde and plots the corresponding KDE
 f = create_kde(kernel, pts, a)
 x = np.linspace(min(pts) - 5, max(pts) + 5, 1000)
 y = [f(xi) for xi in x]
 plt.plot(x, y);

def plot_separate_kernels(kernel, pts, a, norm=False):
 # Plots individual kernels, which are then summed to create the KDE
 x = np.linspace(min(pts) - 5, max(pts) + 5, 1000)
 for pt in pts:
 y = kernel(x, pt, a)
 if norm:
 y /= len(pts)
 plt.plot(x, y)

 plt.show();

plt.xlim(-3, 10)
plt.ylim(0, 0.5)
plt.xlabel("Data")
plt.ylabel("Density")

plot_separate_kernels(gaussian_kernel, data, a = 1)

8.0.1.2.2 步骤 2：将核归一化为总面积为 1

前面我们说每个核的面积为 1。早些时候，我们还说我们的目标是使用这些核构建一个总面积为 1 的 KDE 曲线。如果我们直接将核求和，我们将得到一个积分面积为（5 个核）$\times$（每个 1 的面积）= 5。为了避免这种情况，我们将归一化我们的每个核。这涉及将每个核乘以$1/(\#\text{数据点})$。

在下面的单元格中，我们将我们的 5 个核心中的每一个乘以$\frac{1}{5}$来应用归一化。

代码

plt.xlim(-3, 10)
plt.ylim(0, 0.5)
plt.xlabel("Data")
plt.ylabel("Density")

# The `norm` argument specifies whether or not to normalize the kernels
plot_separate_kernels(gaussian_kernel, data, a = 1, norm = True)

8.0.1.2.3 步骤 3：求和归一化核心

我们的 KDE 曲线是归一化核心的总和。请注意，最终曲线与我们之前看到的sns.kdeplot生成的图相同！

代码

plt.xlim(-3, 10)
plt.ylim(0, 0.5)
plt.xlabel("Data")
plt.ylabel("Density")

plot_kde(gaussian_kernel, data, a = 1)

8.0.1.3 核函数和带宽

一个核心（对我们来说）是一个有效的密度函数。这意味着它：

• 对于所有输入，必须为非负。

• 必须积分为 1。

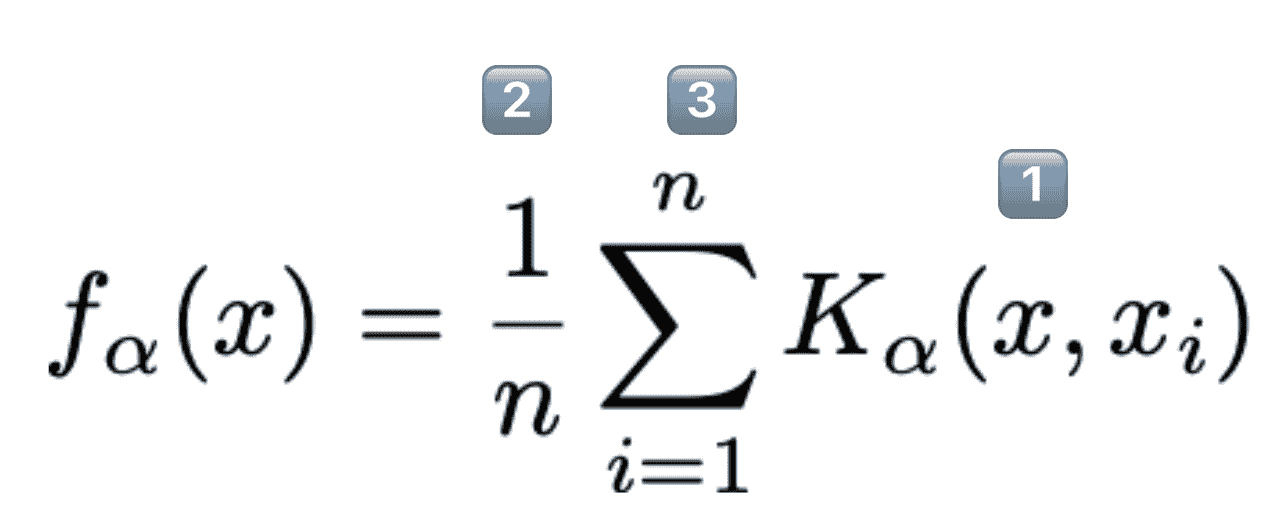
上面给出了一个一般的“KDE 公式”函数。

1. $K_{\alpha }(x,x_i)$是以观察i为中心的核心。

   • 每个核心单独的面积为 1。

   • x 代表数轴上的任何数字。它是我们函数的输入。

2. $n$是我们观察到的数据点的数量。

   • 我们乘以$\frac{1}{n}$，以便 KDE 的总面积仍然为 1。

3. 每个 x i ∈ { x 1 , x 2 , … , x n } x_i \in \{x_1, x_2, \dots, x_n\} xi?∈{x1?,x2?,…,xn?}代表一个观察到的数据点。

   • 这些是我们用来通过对这些点进行多次移位的核心来创建我们的 KDE 的。

$\alpha$（alpha）是带宽或平滑参数。

8.0.1.3.1 高斯核

最常见的核心是高斯核。高斯核等同于以观察值为中心，标准差为（这被称为带宽参数）的高斯概率密度函数。

$$K_a(x,x_i)=\frac{1}{\sqrt{2\pi {\alpha }^2}}{e}^{?\frac{(x?x_i{)}^2}{2{\alpha }^2}}$$

在这个公式中：

• $x$（无下标）代表我们绘图的 x 轴上的值

• $x_i$代表我们数据集中的第$i$个数据点。这是我们在数据采样过程中实际收集到的值之一。在我们之前的例子中，$x_i=2.2$。那些上过概率课的人可能会认出$x_i$是正态分布的均值。

• $\alpha$是带宽参数，代表我们核心的宽度。更正式地说，$\alpha$是高斯曲线的标准差。

这个（令人生畏的）公式的细节不如理解它在核密度估计中的作用重要-这个方程给了我们每个核心的形状。

较大的$\alpha$值会产生一个更宽更短的核心-当这些核心被求和时，这会导致更平滑的 KDE。相反，较小的$\alpha$值会产生一个更窄更高的核心，以及一个更嘈杂的 KDE。

高斯核，$\alpha$ = 0.1

高斯核，$\alpha$ = 1

高斯核，$\alpha$ = 2

高斯核，$\alpha$ = 10

8.0.1.4 矩箱核

核心的另一个例子是矩箱核。矩箱核为观察点内的点分配均匀密度，其他地方的密度为 0。下面的方程是以$x_i$为中心，带宽为$\alpha$的矩箱核。

$$K_a(x,x_i)=\{\begin{array}{ll}\frac{1}{\alpha },& |x?x_i|\le \frac{\alpha }{2}\\ 0,& \text{else?}\end{array}$$

矩箱核在实践中很少使用-我们在这里包括它是为了演示核函数可以采用任何您喜欢的形式，只要它积分为 1 并且不输出负值。

代码

def boxcar_kernel(alpha, x, z):
 return (((x-z)>=-alpha/2)&((x-z)<=alpha/2))/alpha

xs = np.linspace(-5, 5, 200)
alpha=1
kde_curve = [boxcar_kernel(alpha, x, 0) for x in xs]
plt.plot(xs, kde_curve);

以带宽$\alpha$ = 1 为中心的矩箱核。

右侧的图表显示了我们的 5 个数据点数据集使用 Boxcar 核和带宽$\alpha$ = 1 时的密度曲线。

8.0.1.5 深入了解displot

正如我们之前看到的，我们可以使用seaborn的displot函数来绘制各种分布。特别是，displot允许您指定绘图的kind，并且是histplot、kdeplot和ecdfplot的包装器。

下面，我们可以看到一些示例，说明了如何使用sns.displot来绘制各种分布。

首先，我们可以通过将kind设置为"hist"来绘制直方图。请注意，这里我们指定了stat = density，以使直方图归一化，使得直方图下面积等于 1。

sns.displot(data=wb, 
 x="gni", 
 kind="hist", 
 stat="density") # default: stat=count and density integrates to 1
plt.title("Distribution of gross national income per capita");

/Users/Ishani/micromamba/lib/python3.9/site-packages/seaborn/axisgrid.py:118: UserWarning:

The figure layout has changed to tight 

现在，如果我们想生成一个 KDE 图呢？我们可以将kind设置为"kde"！

sns.displot(data=wb, 
 x="gni", 
 kind='kde')
plt.title("Distribution of gross national income per capita");

/Users/Ishani/micromamba/lib/python3.9/site-packages/seaborn/axisgrid.py:118: UserWarning:

The figure layout has changed to tight 

最后，如果我们想生成一个经验累积分布函数（ECDF），我们可以指定kind = "ecdf"。

sns.displot(data=wb, 
 x="gni", 
 kind='ecdf')
plt.title("Cumulative Distribution of gross national income per capita");

/Users/Ishani/micromamba/lib/python3.9/site-packages/seaborn/axisgrid.py:118: UserWarning:

The figure layout has changed to tight 

8.1 定量变量之间的关系

到目前为止，我们已经讨论了如何可视化单变量分布。除此之外，我们还想了解数值变量对之间的关系。

8.1.0.1 散点图

散点图是表示两个定量变量之间关系的最有用的工具之一。它们在评估变量之间的关系强度或相关性方面特别重要。对这些关系的了解可以激发我们建模过程中的决策。

在matplotlib中，我们使用函数plt.scatter来生成散点图。请注意，与我们绘制单变量分布的示例不同，现在我们指定要沿 x 轴和 y 轴绘制的值序列。

plt.scatter(wb["per capita: % growth: 2016"], \
 wb['Adult literacy rate: Female: % ages 15 and older: 2005-14'])

plt.xlabel("% growth per capita")
plt.ylabel("Female adult literacy rate")
plt.title("Female adult literacy against % growth");

在seaborn中，我们调用函数sns.scatterplot。我们使用x和y参数来指示要沿 x 轴和 y 轴绘制的值。通过使用hue参数，我们可以指定用于给每个散点着色的第三个变量。

sns.scatterplot(data = wb, x = "per capita: % growth: 2016", \
 y = "Adult literacy rate: Female: % ages 15 and older: 2005-14", 
 hue = "Continent")

plt.title("Female adult literacy against % growth");

尽管上面的图表传达了两个变量之间的一般关系，但它们都存在一个主要限制——过度绘制。当具有相似值的散点堆叠在一起时，就会发生过度绘制，这使得很难看出实际绘制的散点数量。请注意，在图表的右上方区域，我们无法轻易地判断出有多少点已经被绘制。这使得我们的可视化难以解释。

我们有一些方法可以帮助减少过度绘制：

• 减小散点标记的大小可以提高可读性。我们可以通过将plt.scatter或sns.scatterplot的大小参数s设置为新值来实现这一点。

• 抖动是向所有 x 和 y 值添加少量随机噪声的过程，以略微移动每个数据点的位置。通过随机移动所有数据一小段距离，我们可以更清楚地区分各个点，而不会改变原始数据集的主要趋势。

在下面的单元格中，我们首先使用np.random.uniform对数据进行抖动，然后使用较小的标记重新绘制。结果图更容易解释。

# Setting a seed ensures that we produce the same plot each time
# This means that the course notes will not change each time you access them
np.random.seed(150)

# This call to np.random.uniform generates random numbers between -1 and 1
# We add these random numbers to the original x data to jitter it slightly
x_noise = np.random.uniform(-1, 1, len(wb))
jittered_x = wb["per capita: % growth: 2016"] + x_noise

# Repeat for y data
y_noise = np.random.uniform(-5, 5, len(wb))
jittered_y = wb["Adult literacy rate: Female: % ages 15 and older: 2005-14"] + y_noise

# Setting the size parameter `s` changes the size of each point
plt.scatter(jittered_x, jittered_y, s=15)

plt.xlabel("% growth per capita (jittered)")
plt.ylabel("Female adult literacy rate (jittered)")
plt.title("Female adult literacy against % growth");

8.1.0.2 lmplot和jointplot

seaborn还包括几个内置函数，用于创建更复杂的散点图。其中最常用的两个例子是sns.lmplot和sns.jointplot。

sns.lmplot在一个函数调用中绘制了散点图和线性回归线。我们将在几节课中讨论线性回归。

sns.lmplot(data = wb, x = "per capita: % growth: 2016", \
 y = "Adult literacy rate: Female: % ages 15 and older: 2005-14")

plt.title("Female adult literacy against % growth");

/Users/Ishani/micromamba/lib/python3.9/site-packages/seaborn/axisgrid.py:118: UserWarning:

The figure layout has changed to tight 

sns.jointplot 创建了一个可视化，包括三个组件：散点图、x 值分布的直方图和 y 值分布的直方图。

sns.jointplot(data = wb, x = "per capita: % growth: 2016", \
 y = "Adult literacy rate: Female: % ages 15 and older: 2005-14")

# plt.suptitle allows us to shift the title up so it does not overlap with the histogram
plt.suptitle("Female adult literacy against % growth")
plt.subplots_adjust(top=0.9);

8.1.0.3 六边形图

对于具有大量数据点的数据集，抖动不太可能完全解决重叠绘图的问题。在这种情况下，我们可以尝试通过密度来可视化我们的数据，而不是显示每个单独的数据点。

六边形图可以被看作是显示两个变量之间联合分布的二维直方图。在处理非常密集的数据时，这是特别有用的。在六边形图中，x-y 平面被分成六边形。颜色较深的六边形表示数据的密度更大 - 也就是说，在六边形所围区域内有更多的数据点。

我们可以使用带有kind参数修改的sns.jointplot生成六边形图。

sns.jointplot(data = wb, x = "per capita: % growth: 2016", \
 y = "Adult literacy rate: Female: % ages 15 and older: 2005-14", \
 kind = "hex")

# plt.suptitle allows us to shift the title up so it does not overlap with the histogram
plt.suptitle("Female adult literacy against % growth")
plt.subplots_adjust(top=0.9);

8.1.0.4 等高线图

等高线图是绘制两个变量的联合分布的另一种方式。你可以把它们看作是 KDE 图的二维版本。等高线图可以类似于等高线地图。每条等高线代表一个具有相同数据密度的区域。深色标记的等高线包含更多的数据点（更高的密度）。

如果我们指定了 x 和 y 数据，sns.kdeplot将生成等高线图。

sns.kdeplot(data = wb, x = "per capita: % growth: 2016", \
 y = "Adult literacy rate: Female: % ages 15 and older: 2005-14", \
 fill = True)

plt.title("Female adult literacy against % growth");

8.2 转换

我们现在已经深入研究了可视化，涉及各种形式的可视化、绘图库和高层理论。

这些工作的大部分是为了发现数据中的见解，在课程后期构建数据模型时将证明是必要的。两个变量之间的强烈图形相关性暗示着一个我们可能想要更详细研究的潜在关系。然而，仅依赖于视觉关系是有限的 - 并非所有的图表都显示出关联。异常值和其他统计异常使得难以解释数据。

转换是操纵数据以找到变量之间显著关系的过程。通常通过将数学函数应用于“转换”它们的可能值范围，并突出一些以前隐藏的数据关联来找到这些关系。

要了解为什么我们可能需要转换数据，请考虑以下成年人识字率与国民总收入的图表。

代码

# Some data cleaning to help with the next example
df = pd.DataFrame(index=wb.index)
df['lit'] = wb['Adult literacy rate: Female: % ages 15 and older: 2005-14'] \
 + wb["Adult literacy rate: Male: % ages 15 and older: 2005-14"]
df['inc'] = wb['gni']
df.dropna(inplace=True)

plt.scatter(df["inc"], df["lit"])
plt.xlabel("Gross national income per capita")
plt.ylabel("Adult literacy rate")
plt.title("Adult literacy rate against GNI per capita");

这个图很难解释，原因有两个：

• 可视化中显示的数据似乎几乎“挤压”在一起 - 它在图表的左上方区域非常集中。即使我们对数据集进行了抖动，我们可能也无法完全评估该区域内的所有数据点。

• 很难概括出两个变量之间的明确关系。虽然成年人识字率似乎与国民总收入有一些正向关系，但我们无法详细描述这一趋势的具体情况。

转换将使我们能够更清晰地可视化这些数据，从而使我们能够描述我们感兴趣的变量之间的潜在关系。

我们最常应用变换来线性化变量之间的关系。如果我们找到一个变换使得两个变量的散点图呈线性关系，我们可以“回溯”找到变量之间的确切关系。这在两个主要方面帮助我们。首先，线性关系特别容易解释 - 我们直观地知道线性趋势的斜率和截距代表什么，以及它们如何帮助我们理解两个变量之间的关系。其次，线性关系是线性模型的基础。我们将在下周开始详细探讨线性建模。正如我们将很快看到的，当我们处理线性化的数据时，线性模型变得更加有效。

在本笔记的其余部分，我们将讨论如何对数据集进行线性化，以产生下面的结果。请注意，所得的图显示了 x 和 y 轴上绘制的值之间的粗略线性关系。

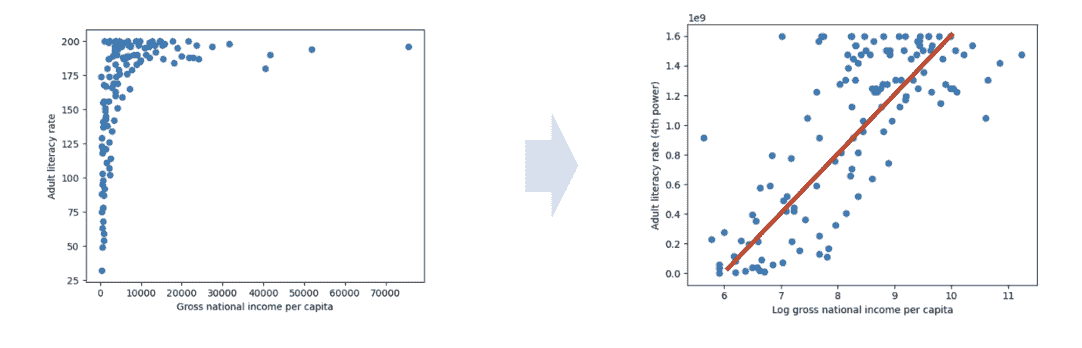
8.2.1 线性化和应用变换

要线性化一个关系，请先问自己：是什么使数据非线性？对于可视化中的每个变量，重复这个问题是有帮助的。

让我们首先考虑上面图中的国民总收入变量。观察散点图中的 y 值，我们可以看到许多大的 y 值都聚集在一起，压缩了垂直轴。水平轴的比例也受到右侧少数大的离群 x 值的影响而被扭曲。

如果我们相对于大部分数据减小这些离群值的大小，我们可以减少水平轴的扭曲。我们如何做到这一点呢？我们需要一个变换，它将：

• 显著减小大 x 值的幅度。

• 不会大幅改变小 x 值的幅度。

产生这种结果的一个函数是对数变换。当我们取一个大数的对数时，原始数值的幅度会急剧减小。相反，当我们取一个小数的对数时，原始数值的值不会发生显著的变化（为了说明这一点，考虑一下$\log (100)=4.61$和$\log (10)=2.3$之间的差异）。

在 Data 100（以及大多数高年级的 STEM 课程）中，$\log$用于指代以$e$为底的自然对数。

# np.log takes the logarithm of an array or Series
plt.scatter(np.log(df["inc"]), df["lit"])

plt.xlabel("Log(gross national income per capita)")
plt.ylabel("Adult literacy rate")
plt.title("Adult literacy rate against Log(GNI per capita)");

在对 x 值取对数之后，我们的图在水平比例上显得更加平衡。我们不再有许多数据点聚集在一端，也没有少数离群值位于极端值。

让我们对 y 值重复这种推理。只考虑图的垂直轴，注意到有许多数据点集中在大的 y 值上。只有少数数据点位于较小的 y 值。

如果我们能够更加“分散”这些大的 y 值，我们将不再看到 y 轴的一个区域中有密集的集中。我们需要一个变换，它将：

• 增加 y 的大值的幅度，使这些数据点在垂直比例上更广泛地分布，

• 不要显著改变 y 的小值的比例（我们不希望大幅修改 y 轴的下限，因为它已经在垂直比例上均匀分布）。

在这种情况下，应用幂变换是有帮助的 - 也就是说，将我们的 y 值提高到一个幂。让我们尝试将成年识字率的值提高到 4 次方。大值提高到 4 次方会比小值提高到 4 次方增加更多的幅度（考虑$2^4=16$和$200^4=1600000000$之间的差异）。

# Apply a log transformation to the x values and a power transformation to the y values
plt.scatter(np.log(df["inc"]), df["lit"]**4)

plt.xlabel("Log(gross national income per capita)")
plt.ylabel("Adult literacy rate (4th power)")
plt.suptitle("Adult literacy rate (4th power) against Log(GNI per capita)")
plt.subplots_adjust(top=0.9);

我们的散点图看起来好多了！现在，我们在水平轴上绘制原始 x 值的对数，垂直轴上绘制原始 y 值的 4 次方。我们开始看到我们转换变量之间的近似线性关系。

我们能从中得出什么？我们现在知道国民总收入的对数和成年识字率的 4 次方大致呈线性关系。如果我们将原始未转换的国民总收入值表示为 $x$，原始成年识字率值表示为 $y$，我们可以使用线性拟合的标准形式来表示这种关系：

$$y^4=m(\log x)+b$$

其中，$m$ 表示线性拟合的斜率，$b$ 表示截距。

下面的单元格计算了我们转换数据的 $m$ 和 $b$。我们将在未来的讲座中讨论这段代码是如何生成的。

代码

# The code below fits a linear regression model. We'll discuss it at length in a future lecture
from sklearn.linear_model import LinearRegression

model = LinearRegression()
model.fit(np.log(df[["inc"]]), df["lit"]**4)
m, b = model.coef_[0], model.intercept_

print(f"The slope, m, of the transformed data is: {m}")
print(f"The intercept, b, of the transformed data is: {b}")

df = df.sort_values("inc")
plt.scatter(np.log(df["inc"]), df["lit"]**4, label="Transformed data")
plt.plot(np.log(df["inc"]), m*np.log(df["inc"])+b, c="red", label="Linear regression")
plt.xlabel("Log(gross national income per capita)")
plt.ylabel("Adult literacy rate (4th power)")
plt.legend();

The slope, m, of the transformed data is: 336400693.43172693
The intercept, b, of the transformed data is: -1802204836.0479977

如果我们想要了解在转换之前我们原始变量之间的潜在关系呢？我们可以简单地重新排列上面的线性表达式！

回想一下我们转换变量 $\log x$ 和 $y^4$ 之间的线性关系。

$$y^4=m(\log x)+b$$

通过重新排列方程，我们找到了未转换变量 $x$ 和 $y$ 之间的关系。

$$y=[m(\log x)+b{]}^{(1/4)}$$

当我们代入上面计算的 $m$ 和 $b$ 的值时，有趣的事情发生了。

代码

# Now, plug the values for m and b into the relationship between the untransformed x and y
plt.scatter(df["inc"], df["lit"], label="Untransformed data")
plt.plot(df["inc"], (m*np.log(df["inc"])+b)**(1/4), c="red", label="Modeled relationship")
plt.xlabel("Gross national income per capita")
plt.ylabel("Adult literacy rate")
plt.legend();

我们已经找到了我们原始变量——国民总收入和成年识字率之间的关系！

转换是了解我们的数据更详细的强大工具。总结我们刚刚取得的成果：

• 我们确定了适当的转换方法来线性化原始数据。

• 我们利用我们对线性曲线的了解来计算转换数据的斜率和截距。

• 我们使用这个斜率和截距信息来推导未转换数据中的关系。

线性化将是我们下周开始线性建模工作的重要工具。

8.2.1.1 图基-莫斯特勒凸起图

图基-莫斯特勒凸起图是确定可能的转换以实现线性关系时的良好指南。它是我们刚刚通过的推理的视觉总结。

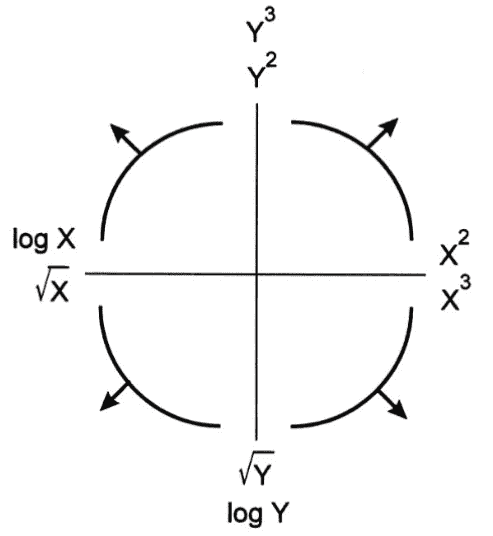
它是如何工作的？每个弯曲的“凸起”代表非线性数据的可能形状。要使用该图，找出四个凸起中哪一个最接近你的数据集。然后，查看该凸起的象限轴。水平轴将列出可能应用于 x 数据线性化的转换。同样，垂直轴将列出可能应用于 y 数据的转换。请注意，每个轴列出两种可能的转换。虽然任何这些转换都有潜力使您的数据集线性化，但请注意这是一个迭代过程。重要的是要尝试这些转换并查看结果，以查看您是否实际实现了线性关系。如果没有，您将需要继续测试其他可能的转换。

一般来说：

• \sqrt{} ? 和 $\log$ 将减少大值的幅度。

• 幂次（${}^2$ 和 ${}^3$）将增加大值的幅度。

重要： 您仍应理解我们通过的逻辑，以确定如何最好地转换数据。凸起图只是对这种推理的总结。您应该能够解释为什么给定的转换是否适合线性化。

8.2.2 附加说明

可视化需要大量思考！

• 有许多用于可视化分布的工具。

  • 单个变量的分布：

    1. Rugplot

    2. 直方图

    3. 密度图

    4. 箱线图

    5. 小提琴图

  • 两个定量变量的联合分布：

    1. 散点图

    2. 六边形图

    3. 等高线图

这门课程主要使用seaborn和matplotlib，但pandas也有基本的内置绘图方法。还有许多其他可视化库，其中plotly就是其中之一。

• plotly非常容易创建交互式图。

• plotly偶尔会出现在讲座代码、实验和作业中！

接下来，我们将深入探讨可视化背后的理论。

8.3 可视化理论

本节标志着本讲座的第二个主要主题-可视化理论。我们将讨论可视化的抽象性质，并分析它们如何传达信息。

记住，我们对可视化数据有两个目标。本节在以下方面尤为重要：

1. 帮助我们理解数据和结果，

2. 与他人交流我们的结果和结论。

8.3.1 信息通道

可视化能够通过各种编码传达信息。在本讲座的其余部分，我们将看看颜色、规模和深度的使用。

8.3.1.1 Rugplots 中的编码

在我们早期讨论 rugplots 时，我们可能忽视了编码的重要性。Rugplots 是有效的可视化，因为它们利用线条粗细来编码频率。考虑以下图表：

8.3.1.2 多维编码

编码也对表示多维数据很有用。注意以下可视化突出了数据的四个不同“维度”：

• X 轴

• Y 轴

• 面积

• 颜色

人类视觉感知系统只能在三维平面上可视化数据，但正如你所见，我们可以编码更多的信息通道。

8.3.2 利用坐标轴

8.3.2.1 考虑数据的规模

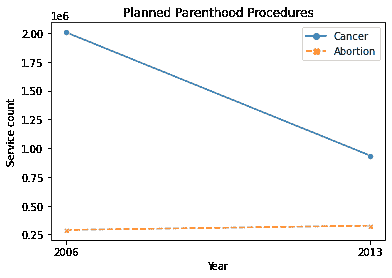
然而，我们应该小心，不要通过操纵比例尺或坐标轴来误传数据中的关系。下面的可视化不正确地描绘了同一图上两个看似独立的关系。作者明显改变了 y 轴的比例尺，以误导他们的观众。

注意向下的线段包含数百万的值，而向上趋势的线段只包含接近三十万的值。这些线段不应该相交。

当数据的数量级差异很大时，建议分析百分比而不是计数。以下图表正确显示了癌症筛查和流产率的趋势。

8.3.2.2 揭示数据

出色的可视化不仅考虑数据的规模，还利用坐标轴以最佳方式传达信息。例如，数据科学家通常设置某些坐标轴限制以突出他们最感兴趣的可视化部分。

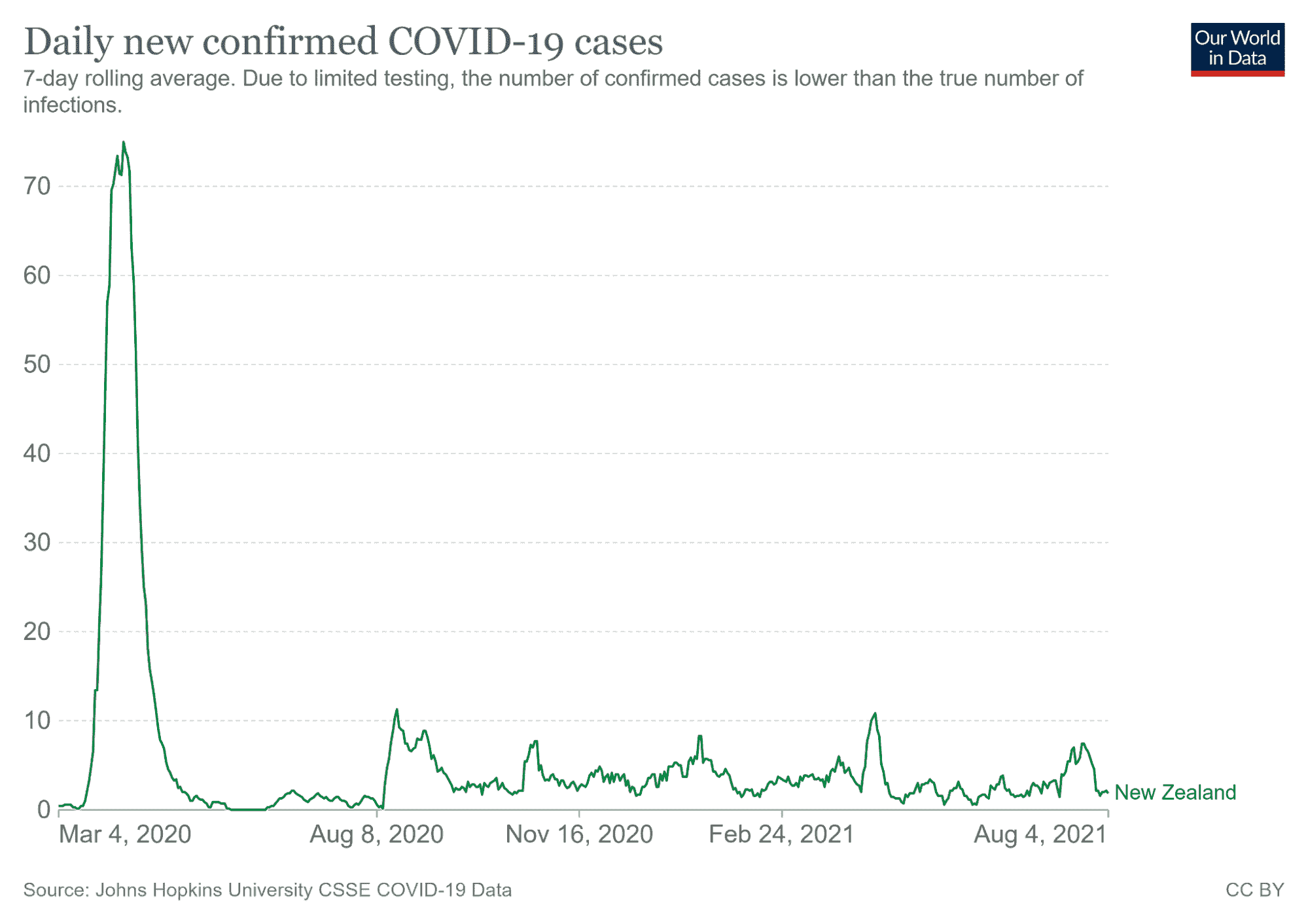
右侧的可视化捕捉了 2020 年 3 月冠状病毒病例的趋势。仅仅通过观察左侧的可视化，观众可能会错误地认为冠状病毒在 2020 年 3 月 4 日开始急剧上升。然而，第二幅插图讲述了一个不同的故事-病例在 2020 年 3 月 21 日左右上升。

8.3.3 利用颜色

颜色是可视化中的另一个重要特征，它的作用远不止看上去的那么简单。

我们已经探讨了在散点图中使用颜色来编码分类变量。现在让我们讨论在新颖的可视化中使用颜色的用途，比如色图和热图。

世界上 5-8%的人是红绿色盲，所以我们必须非常注意我们的配色方案。我们希望尽可能地使这些配色方案易于访问。选择一组能够很好地配合的颜色显然是一项具有挑战性的任务！

8.3.3.1 色图

色图是从像素数据到颜色值的映射，它们经常用于突出图像的不同部分。让我们来研究一下色图的一些特性。

Jet Colormap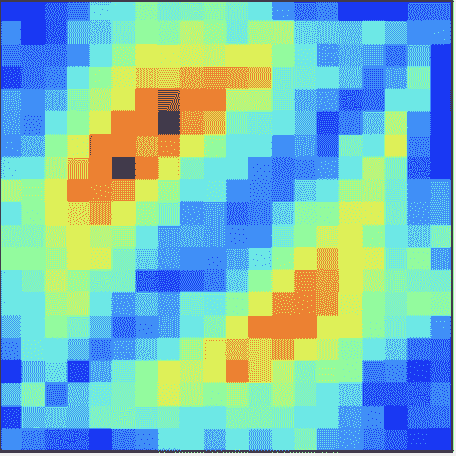

Viridis Colormap

jet 色图因为不是感知均匀而臭名昭著。虽然它看起来比 viridis 更生动，但是激烈的颜色很差地编码了数值数据。为了理解原因，让我们分析以下图像。

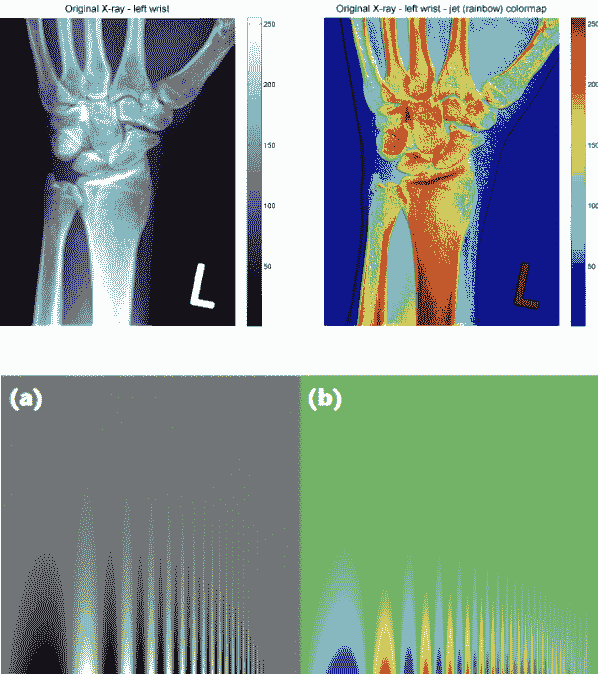
左侧的图表比较了各种色图如何表示从高到低强度的像素数据。这些包括 jet 色图（a 行）和灰度（b 行）。注意灰度图像在平滑过渡像素数据方面做得最好。jet 色图在这方面是最差的 - a 行的四幅图像看起来像是一团独立的颜色。

这种差异在左侧标有(a)和(b)的图像中也是明显的。灰度图像更擅长保留垂直线条中的细节。此外，X 射线扫描中更偏好灰度图像，因为它更加中性。jet 色图中深红色的强度令人恐惧，并且表明出现了问题。

为什么 jet 色图要糟糕得多？答案在于它的颜色组合对人眼的感知。

Jet Colormap Perception

Viridis Colormap Perception

jet 色图在很大程度上是误导性的，因为它不是感知均匀的。感知均匀色图具有这样的特性，即如果像素数据从 0.1 到 0.2，感知变化与数据从 0.8 到 0.9 时的感知变化相同。

注意在 viridis 色图中显示的线性趋势中存在的均匀性。另一方面，jet 色图大部分是非线性的 - 这正是为什么它被认为是一个更糟糕的色图的原因。

8.3.4 利用标记

在我们之前对多维编码的讨论中，我们分析了一个带有四个伪维度的散点图：两个轴，面积和颜色。这些是否适合使用？以下图表分析了人眼在这些“标记”之间的区分能力。

从这张图表中有一些关键的收获

• 长度很容易辨别。不要使用有杂乱基线的图表 - 保持一切与坐标轴对齐。

• 避免使用饼图！角度判断不准确。

• 面积和体积很难区分（面积图，词云等）。

8.3.5 利用条件

条件是比较属于不同组的数据的过程。我们之前在叠加分布，并排箱线图和带有分类编码的散点图中见过这种情况。在这里，我们将介绍正式化这些例子的术语。

考虑一个例子，我们想要分析男性和女性在不同教育水平下的收入。有多种方法可以比较这些数据。

条形图是并列的一个例子：将多个图表并排放置，使用相同的比例尺。散点图是叠加的一个例子：将多个密度曲线和散点图叠加在一起。

哪种更好取决于手头的问题。在这里，叠加使得从一个快速浏览中清楚地看出了精确的工资差异。然而，许多复杂的图表传达的信息更有利于使用并列。下面是一个例子。

8.3.6 利用上下文

一个出色可视化的最后组成部分可能是最关键的 - 使用上下文。添加信息丰富的标题，坐标轴标签和描述性标题都是我们在 Data 8 中一再听到的最佳实践。

一张可发布的图（以及每个 Data 100 图）需要：

• 信息丰富的标题（要点，而不是描述），

• 坐标轴标签，

• 参考线，标记等，

• 图例，如果适用，

• 描述数据的标题，

标题应该：

• 要全面和自包含，

• 描述了图表中的内容，

• 吸引人们注意重要的特征，

• 描述了从图表中得出的结论。

九、抽样

原文：Sampling

译者：飞龙

协议：CC BY-NC-SA 4.0

学习成果

• 了解如何适当地收集数据以帮助回答问题。

在数据科学中，了解人口特征始于拥有质量数据进行调查。虽然通常不可能收集描述人口的所有数据，但我们可以通过适当地从人口中抽样来克服这一问题。在本文中，我们将讨论从人口中抽样的适当技术。

生命周期图

9.1 普查和调查

一般来说：普查是“对人口的官方计数或调查，通常记录个体的各种细节。”一个例子是 2020 年 4 月举行的美国十年一次人口普查。它统计了居住在所有 50 个州、哥伦比亚特区和美国领土的每个人，而不仅仅是公民。法律要求参与（这是由美国宪法规定的）。重要用途包括联邦资金的分配、国会代表权以及划分国会和州立法机构选区。普查由寄往美国不同住房地址的调查组成。

调查是一组问题。一个例子是工作者对个人和家庭进行抽样。提出的问题以及提问的方式可能会影响受访者的回答，甚至可能影响他们是否首先回答。

虽然普查很好，但往往很难和昂贵地对人口中的每个人进行调查。想象一下美国在 2020 年人口普查上花费的资源、金钱、时间和精力。虽然这确实给我们提供了更准确的人口信息，但通常是不可行的。因此，我们通常只对人口的一个子集进行调查。

样本通常是人口的子集，通常用于对人口进行推断。如果我们的样本很好地代表了我们的人口，那么我们可以使用它以较低的成本获取有用信息。也就是说，样本的抽取方式将影响这种推断的可靠性。抽样中的两个常见误差来源是偶然误差，随机样本可能与预期的任何方向不同，以及偏差，这是一个方向上的系统误差。偏差可能是许多因素的结果，例如我们的抽样方案或调查方法。

让我们定义一些有用的词汇：

• 人口：你想了解的群体。

  • 人口中的个体并不总是人。其他人口包括你肠道中的细菌（使用 DNA 测序进行抽样）、某种树木、获得小额贷款的小企业，或者学术期刊或领域中发表的结果。

• 抽样框架：从中抽取样本的列表。

  • 例如，如果抽样人员，则抽样框架是可能最终进入样本的所有人的集合。

• 样本：你最终抽样的对象。因此，样本是你的抽样框架的一个子集。

虽然理想情况下，这三组将完全相同，但实际上通常并非如此。例如，可能有个体在你的抽样框架（因此也在你的样本）中，而不在你的人口中。而且一般来说，样本大小要比人口大小小得多。

抽样框架

9.2 偏差：案例研究

以下案例研究改编自 Freedman、Pisani 和 Purves 的《统计学》，W.W. Norton NY，1978 年。

1936 年，民主党总统富兰克林·D·罗斯福竞选连任，对手是共和党的阿尔夫·兰登。和往常一样，选举前几个月进行了民意调查，试图预测结果。文学文摘是一本成功预测了 1936 年之前 5 次大选结果的杂志。在他们对 1936 年选举的调查中，他们向从电话簿、杂志订阅者名单和乡村俱乐部会员名单中找到的 1000 万人发送了调查。在大约 240 万人中，只有 43%的人报告说他们会投票给罗斯福；因此，文摘预测兰登会获胜。

在选举日，罗斯福以压倒性优势获胜，获得了约 4500 万选民中 61%的普选票。为什么文摘的民意调查会出现如此错误的情况？

事实证明，文学文摘的样本并不代表人口。他们在电话簿、杂志订阅者名单和乡村俱乐部会员名单中找到的样本更富裕，倾向于投票共和党。因此，他们的抽样框架在本质上偏向兰登。文学文摘完全忽视了仍然在大萧条中受苦的大多数选民。此外，他们的回应率很低（约 24%）；谁知道其他未回应者会如何投票？文学文摘在这场灾难后仅 18 个月就倒闭了。

与此同时，正在崛起的统计学家乔治·盖洛普也对 1936 年的选举做出了预测。尽管他的样本量“只有”5 万人（这仍然比必要的要多；我们在讨论中心极限定理时会更多），但他对 56%的选民会选择罗斯福的估计更接近实际结果（61%）。盖洛普还预测了文学文摘的预测，样本量只有 3000 人，通过预测文学文摘的富裕抽样框架并对这些个体进行子抽样，预测了文学文摘的预测，只有 1%的误差。

所以这个故事的寓意是什么？样本虽然方便，但容易受到偶然误差和偏见的影响。选举民意调查，特别是可能涉及许多偏见来源。举几个例子：

• 选择偏见系统性地排除（或偏爱）特定群体。

  • 例如：文学文摘调查排除了不在电话簿上的人。

  • 如何避免：检查抽样框架和抽样方法。

• 回应偏见是因为人们并不总是如实回答。调查设计者特别注意问题的性质和措辞，以避免这种偏见。

  • 例如：非法移民在人口普查调查中被问及公民身份问题时可能不会如实回答。

  • 如何避免：检查问题的性质和调查方法。

• 非响应偏见是因为人们并不总是回应调查请求，这可能会扭曲回应。

  • 例如：只有 1000 万人中的 240 万人回应了文学文摘的调查。

  • 如何避免：保持调查简短，坚持不懈。

今天，盖洛普民意调查是选举结果的主要民意调查之一。许多偏见来源——谁会回答民意调查？选民是否会说实话？我们如何预测投票率？——仍然存在，但盖洛普民意调查采用了几种策略来减轻这些偏见。在他们的抽样框架中，“美国大陆的成年电话家庭的非机构化人口”，他们使用随机数字拨号来包括列出/未列出的电话号码，并避免选择偏见。此外，他们使用了一个在家庭内部的选择过程，随机选择一个或多个成年人的家庭。如果没有人回答，多次重新拨号以避免非响应偏见。

9.3 概率样本

在取样时，关注样本的质量而不是样本的数量至关重要。庞大的样本量并不能弥补糟糕的取样方法。我们的主要目标是收集代表所在人口的样本。在本节中，我们将探讨不同类型的取样及其优缺点。

便利样本是你能够得到的任何样本；这种取样是非随机的。请注意，潦草的取样不一定是随机取样；存在许多潜在的偏差来源。

在概率样本中，我们提供了任何指定的个体集将被选入样本的机会（人口中的个体可以有不同的被选中机会；它们不必全部一致），我们根据这个已知的机会随机取样。因此，概率样本也被称为随机样本。随机性带来了一些好处：

• 因为我们知道源概率，我们可以测量误差。

• 随机取样使我们得到人口更具代表性的样本，从而减少偏见。（注意：只有在我们从中进行取样的概率分布准确时才是这样。使用“糟糕”或不准确的分布进行随机取样可能会产生对人口数量的偏见估计。）

• 概率样本使我们能够估计偏差和机会误差，这有助于我们量化不确定性（在未来的讲座中会详细介绍）。

现实世界通常更加复杂，我们经常不知道最初的概率。例如，我们通常不知道微生物组样本中某个细菌的概率，或者盖洛普打电话时人们是否会接听。尽管如此，我们仍然尽力模拟概率取样，即使取样或测量过程并不完全在我们的控制之下。

一些常见的随机取样方案：

• 带替换的随机样本是一个均匀随机带替换的样本。

  • 随机并不总是意味着“均匀随机”，但在这个特定的上下文中，它是这样的。

  • 人口中的一些个体可能会被多次选中。

• 简单随机样本（SRS）是一个均匀随机不带替换的样本。

  • 每个个体（和个体子集）被选中的机会都是相同的。

  • 每对的机会都与其他每对相同。

  • 每个三元组的机会都与其他三元组相同。

  • 等等。

• 分层随机样本，在这种样本中，对分层（特定群体）进行随机抽样，这些群体一起构成一个样本。

9.3.1 示例方案 1：概率样本

假设我们有 3 个助教（Alan，Bennett，Celine）：我决定按以下方式对其中 2 个进行取样：

• 我以 1.0 的概率选择 A

• 我选择 B 或 C，每个的概率为 0.5。

我们可以在表中列出所有可能的结果及其相应的概率：

结果	概率
{A, B}	0.5
{A, C}	0.5
{B, C}	0

这是一个概率样本（尽管不是很好的样本）。在我的人口中有 3 个人，我知道每个子集的机会。假设我正在测量助教离校园的平均距离。

• 这个方案没有看到整个人口！

• 我使用我取得的单个样本进行估计，这取决于我看到 AB 还是 AC 的机会误差。

• 这个方案对 A 的回应有偏见。

9.3.2 示例方案 2：简单随机样本

考虑以下取样方案：

• 一个班级花名册上按字母顺序列出了 1100 名学生。

• 随机选择名单上的前 10 个学生中的一个（例如学生 8）。

• 要创建你的样本，取那个学生以及其后每 10 个学生（例如学生 8、18、28、38 等）。

这是一个概率样本吗？

是的。对于一个样本[n, n + 10, n + 20, …, n + 1090]，其中 1 <= n <= 10，该样本的概率为 1/10。否则，概率为 0。

只有 10 个可能的样本！ 每个学生被选中的概率相同吗？ 是的。每个学生被选择的概率是 1/10。 这是一个简单随机样本吗？ 不是。选择(8, 18)的机会是 1/10；选择(8, 9)的机会是 0。

9.3.3 演示：Barbie v. Oppenheimer

我们正在尝试从伯克利居民中收集一个样本，以预测 Barbie 和 Oppenheimer 中哪一个在它们的开放日 7 月 21 日表现更好。

首先，让我们获取一个数据集，其中包含伯克利的每个居民（这是一个虚假数据集），以及他们实际在 7 月 21 日观看的电影。

让我们加载movie.csv表。我们可以假设：

• is_male是一个布尔值，表示居民是否认为自己是男性。

• 他们在 7 月 21 日只能观看两部电影：Barbie 和 Oppenheimer。

• 每个居民在 7 月 21 日都会观看一部电影（要么是 Barbie，要么是 Oppenheimer）。

代码

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns

sns.set_theme(style='darkgrid', font_scale = 1.5,
 rc={'figure.figsize':(7,5)})

rng = np.random.default_rng()

movie = pd.read_csv("data/movie.csv")

# create a 1/0 int that indicates Barbie vote
movie['barbie'] = (movie['movie'] == 'Barbie').astype(int)
movie.head()

	age	is_male	movie	barbie
0	35	False	Barbie	1
1	42	True	Oppenheimer	0
2	55	False	Barbie	1
3	77	True	Oppenheimer	0
4	31	False	Barbie	1

伯克利居民中选择 Barbie 的比例是多少？

actual_barbie = np.mean(movie["barbie"])
actual_barbie

0.5302792307692308

这是比赛的实际结果。根据这个结果，Barbie 会获胜。我们的退休人员样本的表现如何？

9.3.3.1 便利样本：退休人员

让我们方便地抽取已经退休的人（年龄>=65 岁）。其中有多少比例的人去看 Barbie 而不是 Oppenheimer？

convenience_sample = movie[movie['age'] >= 65] # take a convenience sample of retirees
np.mean(convenience_sample["barbie"]) # what proportion of them saw Barbie? 

0.3744755089093924

根据这个结果，我们本来会预测 Oppenheimer 会获胜！发生了什么？我们的样本可能太小或者太嘈杂了吗？

# what's the size of our sample? 
len(convenience_sample)

359396

# what proportion of our data is in the convenience sample? 
len(convenience_sample)/len(movie)

0.27645846153846154

看起来我们的样本相当大（大约 360,000 人），所以误差很可能不仅仅是由于偶然性造成的。

9.3.3.2 检查偏差

让我们按年龄汇总所有选择，并可视化按性别分割的 Barbie 观看比例。

votes_by_barbie = movie.groupby(["age","is_male"]).agg("mean", numeric_only=True).reset_index()
votes_by_barbie.head()

	age	is_male	barbie
0	18	False	0.819594
1	18	True	0.667001
2	19	False	0.812214
3	19	True	0.661252
4	20	False	0.805281

代码

# A common matplotlib/seaborn pattern: create the figure and axes object, pass ax
# to seaborn for drawing into, and later fine-tune the figure via ax.
fig, ax = plt.subplots();

red_blue = ["#bf1518", "#397eb7"]
with sns.color_palette(red_blue):
 sns.pointplot(data=votes_by_barbie, x = "age", y = "barbie", hue = "is_male", ax=ax)

new_ticks = [i.get_text() for i in ax.get_xticklabels()]
ax.set_xticks(range(0, len(new_ticks), 10), new_ticks[::10])
ax.set_title("Preferences by Demographics");

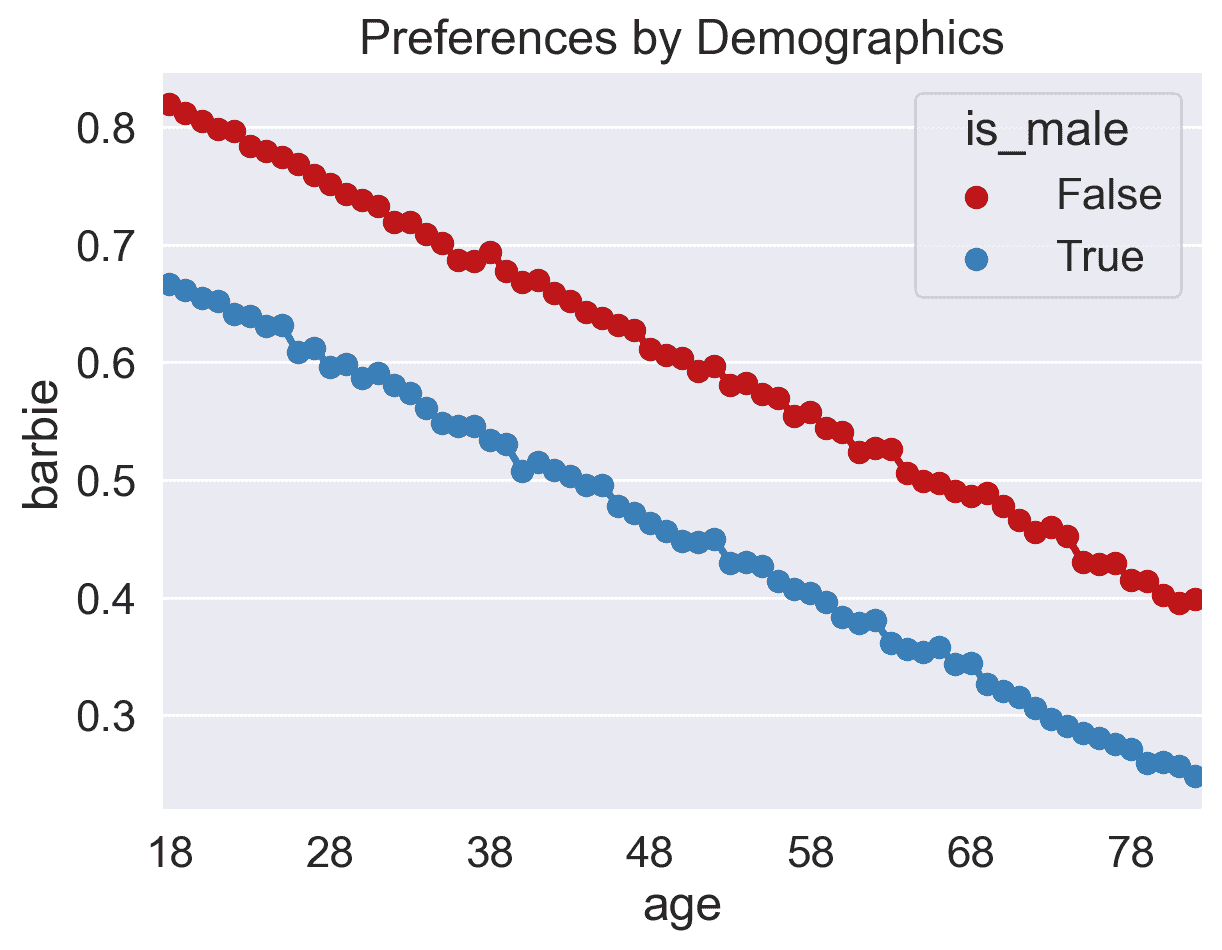
• 我们看到退休人员（在伯克利）倾向于观看 Oppenheimer。

• 我们还看到，认为自己不是男性的居民倾向于喜欢 Barbie。

9.3.3.3 简单随机样本

假设我们取了一个与我们的退休人员样本相同大小的简单随机样本（SRS）：

n = len(convenience_sample)
random_sample = movie.sample(n, replace = False) ## By default, replace = False
np.mean(random_sample["barbie"])

0.5304483077162795

这与 0.5302792307692308 的实际投票结果非常接近！

事实证明，我们可以用更小的样本量（比如 800）得到类似的结果：

n = 800
random_sample = movie.sample(n, replace = False)

# Compute the sample average and the resulting relative error
sample_barbie = np.mean(random_sample["barbie"])
err = abs(sample_barbie-actual_barbie)/actual_barbie

# We can print output with Markdown formatting too...
from IPython.display import Markdown
Markdown(f"**Actual** = {actual_barbie:.4f}, **Sample** = {sample_barbie:.4f}, "
 f"**Err** = {100*err:.2f}%.")

实际 = 0.5303，样本 = 0.5275，误差 = 0.52%。

我们将在本学期后期（重新）学习中心极限定理时学习如何选择这个数字。

9.3.3.4 量化机会误差

在我们的大小为 800 的 SRS 中，我们的机会误差会是多少？

让我们模拟从之前抽取 800 大小的 SRS 的 1000 个版本：

nrep = 1000   # number of simulations
n = 800       # size of our sample
poll_result = []
for i in range(0, nrep):
 random_sample = movie.sample(n, replace = False)
 poll_result.append(np.mean(random_sample["barbie"]))

代码

fig, ax = plt.subplots()
sns.histplot(poll_result, stat='density', ax=ax)
ax.axvline(actual_barbie, color="orange", lw=4);

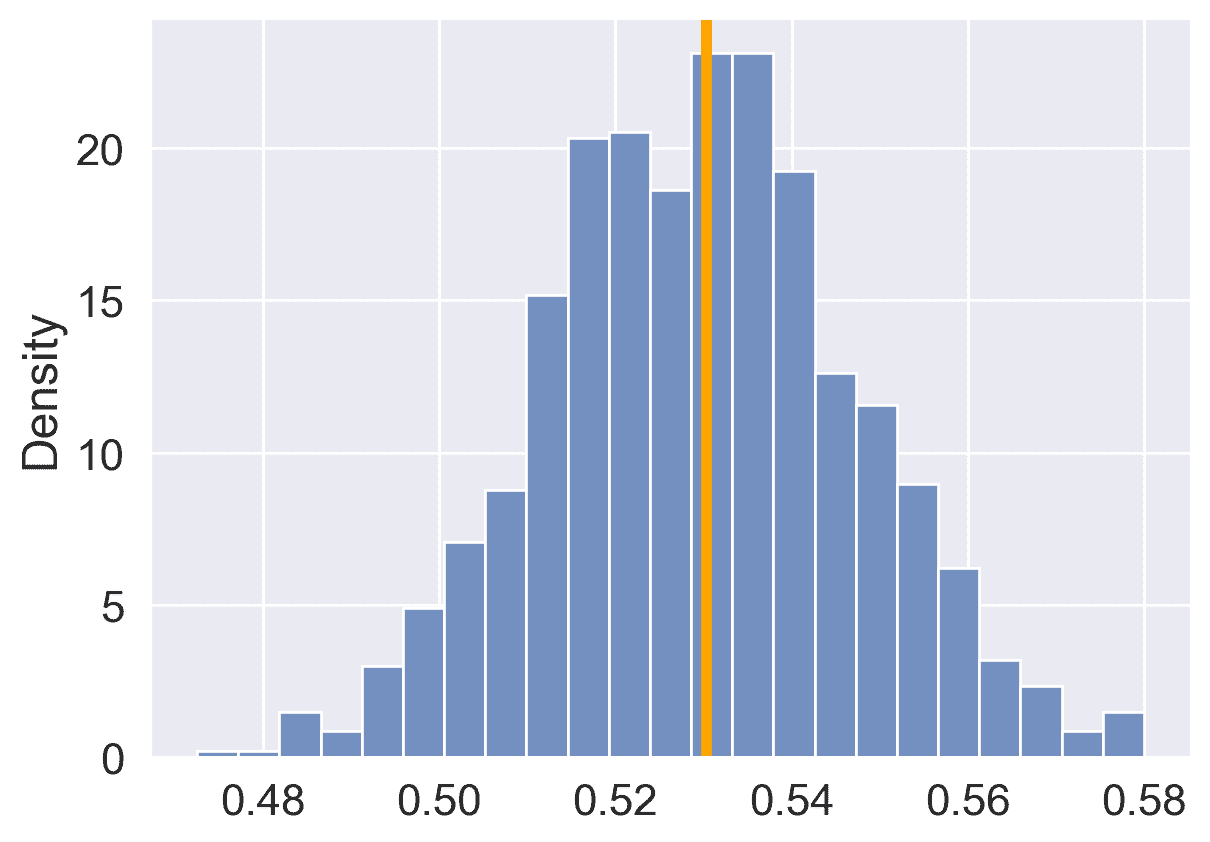
这些模拟样本中有多少比例会预测 Barbie？

poll_result = pd.Series(poll_result)
np.sum(poll_result > 0.5)/1000

0.95

你可以看到曲线看起来大致呈高斯/正态分布。使用 KDE：

代码

sns.histplot(poll_result, stat='density', kde=True);

9.4 总结

了解抽样过程是让我们从描述数据转向理解世界的关键。如果不知道/假设数据是如何收集的，样本和总体之间就没有联系。最终，数据集并不能告诉我们关于数据背后世界的情况。

十、建模简介

原文：Introduction to Modeling

译者：飞龙

协议：CC BY-NC-SA 4.0

学习成果

• 了解模型是什么，以及如何进行四步建模过程。

• 定义损失概念并熟悉$L_1$和$L_2$损失。

• 使用最小化技术拟合简单线性回归模型。**直到本学期为止，我们一直专注于分析数据集。我们已经研究了数据科学生命周期的早期阶段，重点是用于数据分析所需的编程工具、可视化技术和数据清理方法。

这节课标志着关注重点的转变。我们将不再只是检查数据集，而是实际使用我们的数据来更好地理解世界。具体来说，接下来的一系列讲座将探讨预测建模：生成模型以对我们周围的世界进行一些预测。在这节课上，我们将介绍建立建模任务的概念框架。在接下来的几节课中，我们将通过实现各种类型的模型来将这个框架付诸实践。

10.1 什么是模型？

模型是对系统的理想化表示。系统是一组原则或程序，根据这些原则或程序，某事物的运行方式。我们生活在一个充满系统的世界：打开灯的程序是根据一套特定的规则来进行电流流动的。任何事件发生背后的真相通常是复杂的，很多时候具体情况是未知的。世界的运作可以被视为一个巨大的程序。模型试图简化世界，并将其提炼成可操作的部分。

例如：我们将地球上物体的下落建模为受到重力加速度$9.81m/s^2$的恒定加速度。

• 虽然这描述了我们系统的行为，但它只是一个近似。

• 它没有考虑空气阻力、地球重力的局部变化等影响。

• 在实践中，足够准确就足够有用！

10.1.1 建立模型的原因

为什么我们想要建立模型？就数据科学家和统计学家而言，有三个原因，每个原因都意味着对建模的不同关注点。

1. 解释我们生活中发生的复杂现象。例如：

   • 父母的平均身高与子女的平均身高有何关联？

   • 物体的速度和加速度如何影响它的行程？（物理学：$d=d_0+vt+\frac{1}{2}a{t}^2$）

   在这些情况下，我们关心创建简单和可解释的模型，使我们能够理解变量之间的关系。

2. 对未知数据进行准确预测。一些例子包括：

   • 我们能否预测一封电子邮件是否是垃圾邮件？

   • 我们能否对这篇长达 10 页的文章生成一个一句话的摘要？

   在进行预测时，我们更关心做出极其准确的预测，即使以得到一个不可解释的模型为代价。这些有时被称为黑匣子模型，在深度学习等领域很常见。

3. 衡量一个事件对另一个事件的因果效应。例如，

   • 吸烟是否导致肺癌？

   • 职业培训计划是否导致就业和工资增加？

   这是一个更难的问题，因为大多数统计工具都是设计用来推断关联而不是因果关系。我们不会在 Data 100 中专注于这个任务，但如果你感兴趣，可以参加其他关于因果推断的高级课程（例如 Stat 156，Data 102）！

大多数时候，我们的目标是在建立可解释的模型和建立准确模型之间取得平衡。

10.1.2 模型的常见类型

总的来说，模型可以分为两类：

1. 确定性物理（机械）模型：控制世界运行方式的法则。

   • 开普勒的行星运动第三定律（1619）：物体轨道周期的平方与其轨道半长轴的立方的比值对于所有绕同一主体运行的物体都是相同的。

     • $T^2\propto R^3$

   • 牛顿的三大定律：运动和引力（1687）：牛顿的第二定律模拟了物体的质量与加速所需的力之间的关系。

     • $F=ma$

     • $F_g=G\frac{m_1{m}_2}{r^2}$

2. 概率模型：试图理解随机过程如何演变的模型。这些模型更通用，可以用来描述现实世界中的许多现象。这些模型通常对世界的性质做出简化的假设。

   • 泊松过程模型：用于模拟在任何时间点以一定概率发生的随机事件，并且在计数上严格递增，例如顾客到达商店。

注意：这些具体的模型不在 Data 100 的范围内，只是作为动机存在。

10.2 简单线性回归

回归线是最小化所有直线估计的均方误差的唯一直线。与任何直线一样，它可以由斜率和 y-截距定义：

• $\text{斜率}=r?\frac{\text{y?的标准差}}{\text{x?的标准差}}$

• $y\text{-截距}=\text{平均?}y?\text{斜率}?\text{平均?}x$

• $\text{回归估计}=y\text{-截距}+\text{斜率}?x$

• $\text{残差}=\text{观察到的?}y?\text{回归估计}$

代码

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Set random seed for consistency 
np.random.seed(43)
plt.style.use('default') 

#Generate random noise for plotting
x = np.linspace(-3, 3, 100)
y = x * 0.5 - 1 + np.random.randn(100) * 0.3

#plot regression line
sns.regplot(x=x,y=y);

10.2.1 符号和定义

对于表示我们的数据 $\mathcal{D}=\{(x_1,y_1),(x_2,y_2),\dots ,(x_n,y_n)\}$ 的一对变量 $x$ 和 $y$，我们将它们的均值/平均值表示为 $\bar{x}$ 和 $\bar{y}$，标准差表示为 ${\sigma }_x$ 和 ${\sigma }_y$。

10.2.1.1 标准单位

如果以下条件成立，则变量以标准单位表示：

1. 标准单位中的 0 等于原始变量单位中的均值 ($\bar{x}$)。

2. 1 个标准单位的增加等于原始变量单位中的 1 个标准差 (${\sigma }_x$) 的增加。

要将变量 $x_i$ 转换为标准单位，我们从其均值中减去它，并将其除以其标准差。例如，标准单位中的 $x_i$ 是 $\frac{x_i?\bar{x}}{{\sigma }_x}$。

10.2.1.2 相关性

相关性 ($r$) 是以标准单位测量的 $x$ 和 $y$ 的乘积的平均值。

$$r=\frac{1}{n}\sum _{i=1}^n(\frac{x_i?\bar{x}}{{\sigma }_x})(\frac{y_i?\bar{y}}{{\sigma }_y})$$

1. 相关性衡量了两个变量之间的线性关联的强度。

2. 相关性在-1 和 1 之间变化：$r\le 1$, with $r=1$ 表示完美的线性关联，$r=?1$ 表示完美的负相关。 $r$ 越接近于 $0$, 线性关联越弱。

3. 相关性不能说明因果关系和非线性关联。相关性不意味着因果关系。当 $r=0$ 时，两个变量是不相关的。然而，它们仍然可以通过一些非线性关系相关。

代码

def plot_and_get_corr(ax, x, y, title):
 ax.set_xlim(-3, 3)
 ax.set_ylim(-3, 3)
 ax.set_xticks([])
 ax.set_yticks([])
 ax.scatter(x, y, alpha = 0.73)
 r = np.corrcoef(x, y)[0, 1]
 ax.set_title(title + " (corr: {})".format(r.round(2)))
 return r

fig, axs = plt.subplots(2, 2, figsize = (10, 10))

# Just noise
x1, y1 = np.random.randn(2, 100)
corr1 = plot_and_get_corr(axs[0, 0], x1, y1, title = "noise")

# Strong linear
x2 = np.linspace(-3, 3, 100)
y2 = x2 * 0.5 - 1 + np.random.randn(100) * 0.3
corr2 = plot_and_get_corr(axs[0, 1], x2, y2, title = "strong linear")

# Unequal spread
x3 = np.linspace(-3, 3, 100)
y3 = - x3/3 + np.random.randn(100)*(x3)/2.5
corr3 = plot_and_get_corr(axs[1, 0], x3, y3, title = "strong linear")
extent = axs[1, 0].get_window_extent().transformed(fig.dpi_scale_trans.inverted())

# Strong non-linear
x4 = np.linspace(-3, 3, 100)
y4 = 2*np.sin(x3 - 1.5) + np.random.randn(100) * 0.3
corr4 = plot_and_get_corr(axs[1, 1], x4, y4, title = "strong non-linear")

plt.show()

10.2.2 替代形式

当变量 $y$ 和 $x$ 以标准单位测量时，用于预测 $y$ 的回归线具有斜率 $r$ 并通过原点。

$${\hat{y}}_{su}=r?x_{su}$$

• 在原始单位中，这变为

$$\frac{\hat{y}?\bar{y}}{{\sigma }_y}=r?\frac{x?\bar{x}}{{\sigma }_x}$$

10.2.3 推导

从顶部开始，我们有我们所要求的回归线的形式，并且我们希望表明它等价于最佳线性回归线：$\hat{y}=\hat{a}+\hat{b}x$。

回想一下：

• KaTeX parse error: Unexpected end of input in a macro argument, expected '}' at end of input: …}{\text{x 的标准差}

• $\hat{a}=y的平均值?\text{斜率}?x的平均值$

证明：

$$\frac{\hat{y}?\bar{y}}{{\sigma }_y}=r?\frac{x?\bar{x}}{{\sigma }_x}$$

乘以${\sigma }_y$，并在两边加上$\bar{y}$。

$$\hat{y}={\sigma }_y?r?\frac{x?\bar{x}}{{\sigma }_x}+\bar{y}$$

将系数${\sigma }_y?r$分配给$\frac{x?\bar{x}}{{\sigma }_x}$项

$$\hat{y}=(\frac{r{\sigma }_y}{{\sigma }_x})?x+(\bar{y}?(\frac{r{\sigma }_y}{{\sigma }_x})\bar{x})$$

现在我们看到我们有一条符合我们要求的线：

• 斜率：$r?\frac{\text{y?的标准差}}{\text{x?的标准差}}=r?\frac{{\sigma }_y}{{\sigma }_x}$

• 截距：$\bar{y}?\text{斜率}?\bar{x}$

请注意，第 i 个数据点的误差为：$e_i=y_i?\widehat{y_i}$

10.3 建模过程

在高层次上，模型是表示系统的一种方式。在 Data 100 中，我们将把模型视为我们用来描述变量之间关系的一些数学规则。

我们正在对哪些变量进行建模？通常，我们使用我们收集到的样本数据中的变量子集来对该数据中的另一个变量进行建模。更正式地说，假设我们有以下数据集$\mathcal{D}$：

$$\mathcal{D}=\{(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\}$$

每一对值$(x_i,y_i)$代表一个数据点。在建模环境中，我们称这些为观察。$y_i$是我们试图对其进行建模的因变量，也称为输出或响应。$x_i$是输入到模型中进行预测的自变量，也称为特征。

我们建模的目标是使用观察到的数据$\mathcal{D}$来预测输出变量$y_i$。我们将每个预测表示为${\hat{y}}_i$（读作：“y 帽下标 i”）。

我们如何生成这些预测？在接下来的几堂课中，我们将遇到一些模型的例子如下：

$${\hat{y}}_i=\theta$$

$${\hat{y}}_i={\theta }_0+{\theta }_1{x}_i$$

上面的例子被称为参数模型。它们将收集到的数据$x_i$与我们做出的预测${\hat{y}}_i$联系起来。一些参数($\theta$, ${\theta }_0$, ${\theta }_1$)用于描述$x_i$和${\hat{y}}_i$之间的关系。

请注意，我们并不立即知道这些参数的值。虽然特征$x_i$是从我们观察到的数据中获取的，但我们需要决定给$\theta$、${\theta }_0$和${\theta }_1$什么值。这是参数建模的核心：我们应该选择什么参数值，使我们的模型能够做出最佳的预测？

选择我们的模型参数，我们将通过建模过程来进行。

1. 选择模型：我们应该如何表示世界？

2. 选择损失函数：我们如何量化预测误差？

3. 拟合模型：在给定数据的情况下，我们如何选择模型的最佳参数？

4. 评估模型性能：我们如何评估这个过程是否产生了一个好的模型？

10.4 选择模型

我们的第一步是选择一个模型：定义描述特征$x_i$和预测${\hat{y}}_i$之间关系的数学规则。

在Data 8中，您学习了简单线性回归（SLR）模型。您学到了该模型的形式：$${\hat{y}}_i=a+b{x}_i$$

在 Data 100 中，我们将使用略有不同的符号：我们将用${\theta }_0$替换$a$，用${\theta }_1$替换$b$。这将使我们能够在课程后期探索更复杂的模型时使用相同的符号。

$${\hat{y}}_i={\theta }_0+{\theta }_1{x}_i$$

SLR 模型的参数是 ${\theta }_0$，也称为截距项，和 ${\theta }_1$，也称为斜率项。为了创建一个有效的模型，我们希望选择 ${\theta }_0$ 和 ${\theta }_1$ 的值，以最准确地预测输出变量。 “最佳”拟合模型参数被赋予特殊名称：${\hat{\theta }}_0$ 和 ${\hat{\theta }}_1$；它们是允许我们的模型生成最佳可能预测的特定参数值。

在 Data 8 中，您学到了最佳 SLR 模型参数是：$${\hat{\theta }}_0=\bar{y}?{\hat{\theta }}_1\bar{x}{\hat{\theta }}_1=r\frac{{\sigma }_y}{{\sigma }_x}$$

关于符号的快速提醒：

• $\bar{y}$ 和 $\bar{x}$ 分别表示 $y$ 和 $x$ 的均值

• ${\sigma }_y$ 和 ${\sigma }_x$ 表示 $y$ 和 $x$ 的标准偏差

• $r$ 是相关系数，定义为 $x$ 和 $y$ 的乘积的平均值，以标准单位测量：$\frac{1}{n}{\sum }_{i=1}^n(\frac{x_i?\bar{x}}{{\sigma }_x})(\frac{y_i?\bar{y}}{{\sigma }_y})$

在 Data 100 中，我们想要了解如何推导出这些最佳模型系数。为此，我们将介绍损失函数的概念。

10.5 选择损失函数

我们已经讨论了创建“最佳”预测的想法。这引出了一个问题：我们如何决定我们模型的预测是“好”还是“坏”？

损失函数 描述了特定模型或模型参数选择所产生的成本、误差或拟合。这个函数，$L(y,\hat{y})$，量化了我们模型的单个预测与我们收集的数据中真实观测值之间的“坏”或“偏离”程度。

特定模型的损失函数的选择将影响估计的准确性和计算成本，并且还将取决于手头的估计任务。例如，

• 输出是定量的还是定性的？

• 异常值重要吗？

• 所有错误一样昂贵吗？（例如，癌症测试的假阴性可能比假阳性更危险）

无论使用的具体函数是什么，损失函数应遵循两个基本原则：

• 如果预测 ${\hat{y}}_i$ 接近 实际值 $y_i$，损失应该很低。

• 如果预测 ${\hat{y}}_i$ 与实际值 $y_i$ 相距很远，损失应该很高。

损失函数的两种常见选择是平方损失和绝对损失。

平方损失，也称为L2 损失，计算观测到的 $y_i$ 和预测的 ${\hat{y}}_i$ 之间的差的平方：$$L(y_i,{\hat{y}}_i)=(y_i?{\hat{y}}_i{)}^2$$

绝对损失，也称为L1 损失，计算观测到的 $y_i$ 和预测的 ${\hat{y}}_i$ 之间的绝对差：$$L(y_i,{\hat{y}}_i)=|y_i?{\hat{y}}_i|$$

L1 和 L2 损失为我们提供了一种工具，用于量化我们模型在单个数据点上的表现。这是一个很好的开始，但是理想情况下，我们希望了解我们的模型在整个数据集上的表现。一个自然的方法是计算数据集中所有数据点的平均损失。这被称为成本函数，$\hat{R}(\theta )$：$$\hat{R}(\theta )=\frac{1}{n}\sum _{i=1}^{n}L(y_i,{\hat{y}}_i)$$

在统计文献中，成本函数有许多名称。您可能还会遇到以下术语：

• 经验风险（这就是我们给成本函数命名为 $R$ 的原因）

• 错误函数

• 平均损失

我们可以将我们的 L1 和 L2 损失代入成本函数的定义中。均方误差（MSE） 是数据集中平均平方损失：$$\text{MSE}=\frac{1}{n}\sum _{i=1}^n(y_i?{\hat{y}}_i{)}^2$$

平均绝对误差（MAE） 是数据集中平均绝对损失：$$\text{MAE}=\frac{1}{n}\sum _{i=1}^n|y_i?{\hat{y}}_i|$$

10.6 拟合模型

现在我们已经建立了损失函数的概念，我们可以回到选择模型参数的原始目标。具体来说，我们希望选择最佳的模型参数集，以最小化模型在数据集上的成本。这个过程称为拟合模型。

我们知道从微积分中，当一个函数的一阶导数等于零，二阶导数为正时，函数达到最小值。我们经常称被最小化的函数为目标函数（我们的目标是找到它的最小值）。

为了找到最佳的模型参数，我们：

1. 对成本函数分别对该参数求导

2. 将导数设为 0

3. 解出参数

我们对模型中每个参数重复这个过程。现在，我们将忽略二阶导数条件。

为了帮助我们理解这个过程，让我们通过使用均方误差作为成本函数，推导简单线性回归的最优模型参数。记住：尽管符号可能看起来复杂，但我们所做的只是按照上面的三个步骤进行操作！

步骤 1：对成本函数分别对每个模型参数求导。我们将 SLR 模型${\hat{y}}_i={\theta }_0+{\theta }_1{x}_i$代入上述 MSE 的定义中，并对${\theta }_0$和${\theta }_1$进行微分。

$$\frac{?}{?{\theta }_0}\text{MSE}=\frac{?2}{n}\sum _{i=1}^n{y}_i?{\theta }_0?{\theta }_1{x}_i$$

$$\frac{?}{?{\theta }_1}\text{MSE}=\frac{?2}{n}\sum _{i=1}^n(y_i?{\theta }_0?{\theta }_1{x}_i)x_i$$

让我们更深入地走一遍这些推导，从对${\theta }_0$的 MSE 的导数开始。

根据上面的 MSE，我们知道：$$\frac{?}{?{\theta }_0}\text{MSE}=\frac{?}{?{\theta }_0}\frac{1}{n}\sum _{i=1}^n{(y_i?{\theta }_0?{\theta }_1{x}_i)}^2$$

注意，求和的导数等于导数的和，这样就变成了：$$=\frac{1}{n}\sum _{i=1}^n\frac{?}{?{\theta }_0}{(y_i?{\theta }_0?{\theta }_1{x}_i)}^2$$

然后，我们可以应用链式法则。

$$=\frac{1}{n}\sum _{i=1}^{n}2?(y_i?{\theta }_0?{\theta }_1{x}_i)\dot{(}?1)$$

最后，我们可以简化常数，得到我们的答案。

$$\frac{?}{?{\theta }_0}\text{MSE}=\frac{?2}{n}\sum _{i=1}^n(y_i?{\theta }_0?{\theta }_1{x}_i)$$

按照同样的步骤，我们可以对${\theta }_1$的 MSE 进行求导。

$$\frac{?}{?{\theta }_1}\text{MSE}=\frac{?}{?{\theta }_1}\frac{1}{n}\sum _{i=1}^n{(y_i?{\theta }_0?{\theta }_1{x}_i)}^2$$

$$=\frac{1}{n}\sum _{i=1}^n\frac{?}{?{\theta }_1}{(y_i?{\theta }_0?{\theta }_1{x}_i)}^2$$

$$=\frac{1}{n}\sum _{i=1}^{n}2\dot{(y_i?{\theta }_0?{\theta }_1{x}_i)}\dot{(}?x_i)$$

$$=\frac{?2}{n}\sum _{i=1}^n(y_i?{\theta }_0?{\theta }_1{x}_i)x_i$$

步骤 2：将导数设为 0。简化项后，这产生了两个估计方程。模型参数的最佳集合$({\hat{\theta }}_0,{\hat{\theta }}_1)$ 必须满足这两个最优性条件。$$0=\frac{?2}{n}\sum _{i=1}^n{y}_i?{\hat{\theta }}_0?{\hat{\theta }}_1{x}_i?\frac{1}{n}\sum _{i=1}^n{y}_i?{\hat{y}}_i=0$$

$$0=\frac{?2}{n}\sum _{i=1}^n(y_i?{\hat{\theta }}_0?{\hat{\theta }}_1{x}_i)x_i?\frac{1}{n}\sum _{i=1}^n(y_i?{\hat{y}}_i)x_i=0$$

步骤 3：解估计方程以计算${\hat{\theta }}_0$和${\hat{\theta }}_1$的估计值。

取第一个方程式给出了${\hat{\theta }}_0$的估计值：$$\frac{1}{n}\sum _{i=1}^n{y}_i?{\hat{\theta }}_0?{\hat{\theta }}_1{x}_i=0$$

$$\left(\frac{1}{n}\sum _{i=1}^n{y}_i\right)?{\hat{\theta }}_0?{\hat{\theta }}_1\left(\frac{1}{n}\sum _{i=1}^n{x}_i\right)=0$$

$${\hat{\theta }}_0=\bar{y}?{\hat{\theta }}_1\bar{x}$$

通过稍微调整，第二个方程给出了 ${\hat{\theta }}_1$ 的估计值。首先将第一个估计方程乘以 $\bar{x}$，然后从第二个估计方程中减去结果。

$$\frac{1}{n}\sum _{i=1}^n(y_i?{\hat{y}}_i)x_i?\frac{1}{n}\sum _{i=1}^n(y_i?{\hat{y}}_i)\bar{x}=0$$

$$\frac{1}{n}\sum _{i=1}^n(y_i?{\hat{y}}_i)(x_i?\bar{x})=0$$

接下来，代入 ${\hat{y}}_i={\hat{\theta }}_0+{\hat{\theta }}_1{x}_i=\bar{y}+{\hat{\theta }}_1(x_i?\bar{x})$：

$$\frac{1}{n}\sum _{i=1}^n(y_i?\bar{y}?{\hat{\theta }}_1(x?\bar{x}))(x_i?\bar{x})=0$$

$$\frac{1}{n}\sum _{i=1}^n(y_i?\bar{y})(x_i?\bar{x})={\hat{\theta }}_1\times \frac{1}{n}\sum _{i=1}^n(x_i?\bar{x}{)}^2$$

通过使用相关性的定义 $\left(r=\frac{1}{n}{\sum }_{i=1}^n(\frac{x_i?\bar{x}}{{\sigma }_x})(\frac{y_i?\bar{y}}{{\sigma }_y})\right)$ 和标准差 $\left({\sigma }_x=\sqrt{\frac{1}{n}{\sum }_{i=1}^n(x_i?\bar{x}{)}^2}\right)$，我们可以得出结论：$$r{\sigma }_x{\sigma }_y={\hat{\theta }}_1\times {\sigma }_x^2$$

$${\hat{\theta }}_1=r\frac{{\sigma }_y}{{\sigma }_x}$$

就像在 Data 8 中给出的那样！

记住，这个推导是在使用 MSE 成本函数时找到了 SLR 的最佳模型参数。如果我们使用了不同的模型或不同的损失函数，我们很可能会找到最佳模型参数的不同值。然而，无论使用什么模型和损失，我们总是可以遵循这三个步骤来拟合模型。