CGAL的三角形曲面网格的最短路径
????????该软件包提供了一种计算三角曲面网格上测地线最短路径的算法。?
????????CGAL的Surface_mesh_shortest_path的原理是基于测地线最短路径算法。测地线是连接两个点之间的最短路径,它沿着曲面的法线方向前进。在三角曲面网格上,测地线算法可以用于找到从一点到另一点的最短路径。

?????????使用由绿色正方形表示的一个源点的地形上的最短路径。?
1、介绍
????????机器人跨越三维地形表面的运动规划是最短路径计算的一个典型应用。使用二维近似无法捕捉到我们试图跨越的地形中任何有趣的东西,并且会给出糟糕的解决方案。这个问题通常被称为离散测地线问题。尽管这个问题的更一般版本,即存在障碍物的三维中最短路径,是NP难的,但当运动被限制在物体的二维表面时,它可以有效地解决。
????????该软件包中实现的算法构建了一个数据结构,可以有效地回答以下形式的查询:给定一个三角网格曲面M、M上的一组源点S和M上的目标点t,找到t和S中任意元素之间的最短路径λ,其中λ被限制在M的表面上。
????????使用的算法基于 Xin 和 Wang 的论文,这是一种快速实用的算法,用于精确计算测地线最短路径。它是 Chen 和 Han? 以及 Mitchell、Mount 和 Papadimitriou 早期结果的扩展。
????????此软件包与“热方法”软件包相关。两者都处理测地线距离。测地线最短路径软件包计算曲面任意两点之间的精确最短路径。热方法软件包计算网格的每个顶点到一或多个源顶点的近似距离。
2、接口
2.1、曲面网格最短路径类
????????此包的主要类是Surface_mesh_shortest_path。在下文中,我们描述了使用此类时的典型工作流
指定输入
????????最短路径是在由 FaceListGraph 概念的模型表示的三角化表面网格上计算的。对输入表面网格的 属性、连通性或凸性没有限制。
????????出于效率原因,内部使用顶点、半边和面的索引属性映射。对于每个单形类型,属性映射必须在 0 和单形数量之间提供一个索引。我们建议使用 CGAL::Surface_mesh 作为 FaceListGraph 的模型。
????????如果您使用 class administrativel::Polyhedron_3,您应该将其与项类 CGAL::Polyhedron_items_with_id_3,它提供了默认的属性映射。此项目类与每个单形关联,提供了一个 O(1) 时间访问索引。请注意,属性映射的初始化需要调用 set_halfedgeds_items_id()。
????????每个顶点的嵌入访问是通过使用点顶点属性映射完成的,该映射将每个顶点与一个3D点相关联。为CGAL类提供了默认值。
????????如果使用的 traits 类包含一些本地状态,则必须在构造它时将其传递给类(默认提供的类则不需要)。
指定源点
????????最短路径查询的源点集可以逐个填充或使用范围填充。可以使用输入曲面网格的顶点或具有某些重心坐标的输入曲面网格的面来指定源点。给定位于三角形面(A,B,C)内的点p,其重心坐标是权重三元组(b0,b1,b2),使得p=b0? A+b1? B+b2? C,并且b0+b1+b2=1。
????????为了方便起见,提供了一个函数 Surface_mesh_shortest_path::locate(),用于根据几何输入构造面位置:
????????给定一个位于3D空间中的点p,该函数计算曲面上最接近p的点,并返回包含该点的面及其重心坐标;
? ? ? ? 给定一条位于三维空间中的射线r,该函数计算射线与曲面的交点,并且(如果存在交点)返回包含该点的面,以及它的重心坐标;
构建内部序列树
????????最短路径查询的耗时操作在于构建用于进行查询的内部数据结构。这个数据结构被称为序列树。当第一个最短路径查询完成时,它将自动构建,并且只要源点集不变,它将重新用于任何后续查询。每次源点集发生变化时,都需要重建序列树(如果已经构建)。请注意,它也可以通过调用 Surface_mesh_shortest_path::build_sequence_tree() 手动构建。
最短路径查询
????????至于指定源点,最短路径查询的目标点可以使用输入曲面网格的顶点或输入曲面网格的面和一些重心坐标来指定。
????????有三种不同类型的查询函数可以使用类 Surface_mesh_shortest_path 调用。给定一个目标点,所有这些函数计算该目标点与源点集之间的最短路径:
????????Surface_mesh_shortest_path::shortest_distance_to_source_points() 提供最接近目标点的源点以及最短路径的长度。
????????Surface_mesh_shortest_path::shortest_path_points_to_source_points() 提供最短路径与输入曲面网格的边和顶点的所有交点(包括源点和目标点)。该函数对于可视化目的很有用。
????????Surface_mesh_shortest_path::shortest_path_sequence_to_source_points 使用 SurfaceMeshShortestPathVisitor 概念的访问者对象模型,可以访问最短路径所穿越的简单体的完整序列。
额外的便利功能
????????提供了一些方便的函数来计算:
????????指定为输入曲面网格的面的输入曲面网格上的点和一些重心坐标。
????????输入表面网格上距离给定3D点最近的点(指定为输入表面网格的面和一些重心坐标)。这些函数使用类CGAL::AABB_tree。
2.2、内核建议
????????简而言之,我们建议使用具有精确谓词的CGAL内核,例如CGAL::Exact_predicates_inexact_constructions_kernel。
????????如果你需要精确的构造(例如最短路径点计算),你应该使用具有精确构造的内核。虽然该算法使用平方根运算,但它也可以在不支持平方根的几何内核上工作,方法是首先使用std::sqrt将内核的数字类型转换为double,然后再转换回来。请注意,最好使用直接支持平方根的内核,以获得最精确的最短路径计算。
????????使用此软件包中的一个内核,如CGAL::Exact_predicates_exact_constructions_kernel_with_sqrt,确实可以提供精确的最短路径,但速度非常慢。
????????事实上,为了计算沿表面的距离,有必要将面序列展开,边对边,展开到一个公共平面。 SurfaceMeshShortestPath Traits::Construct_triangle_3_to_triangle_2_projection 函子通过将给定面旋转到 xy 平面,提供了序列中第一个面的初始布局。
????????SurfaceMeshShortestPath Traits::Construct_triangle_3_along_segment_2_flattening 使用指定的段作为基底,将三角形展开到平面中。由于这会在平面上产生一系列构造的三角形,因此使用此内核(CORE::Expr 或 leda_real)的精确表示类型将处理非常慢,即使在非常简单的输入上。这是因为精确表示将有效地为每次计算增加一个 O(n) 因数。
3、基准
????????这些基准测试是在多次试验中使用随机生成的源点和目的点运行的。在Cygwin 1.7.32下,使用CGAL 4.5执行测量,使用Gnu C++编译器版本4.8.3,选项-O3-DNDEBUG。使用的系统是64位Intel Core i3 2.20GHz处理器,具有6GB RAM
3.1、单一源点
| Model | Number of Vertices | Average Construction Time (s) | Average Queries Per Second | Peak Memory Usage (MB) |
|---|---|---|---|---|
| ellipsoid.off | 162 | 0.00258805 | 1.21972e+06 | 0.39548 |
| anchor.off | 519 | 0.0580262 | 230461 | 3.88799 |
| rotor.off | 600 | 0.0386633 | 326175 | 3.10571 |
| spool.off | 649 | 0.0418305 | 299766 | 3.75773 |
| handle.off | 1165 | 0.0976167 | 227343 | 7.66706 |
| couplingdown.off | 1841 | 0.138467 | 246833 | 10.1731 |
| bones.off | 2154 | 0.0101125 | 1.31834e+06 | 0.865896 |
| mushroom.off | 2337 | 0.206034 | 202582 | 22.5804 |
| elephant.off | 2775 | 0.136177 | 313785 | 14.0987 |
| cow.off | 2904 | 0.259104 | 206515 | 17.4796 |
| knot1.off | 3200 | 0.279455 | 207084 | 25.314 |
| retinal.off | 3643 | 0.255788 | 247617 | 29.8031 |
| femur.off | 3897 | 0.25332 | 264825 | 21.4806 |
| knot2.off | 5760 | 0.295655 | 309593 | 22.5549 |
| bull.off | 6200 | 0.513506 | 209994 | 34.983 |
| fandisk.off | 6475 | 0.609507 | 198768 | 71.3617 |
| lion-head.off | 8356 | 1.23863 | 145810 | 86.6908 |
| turbine.off | 9210 | 2.23755 | 93079.5 | 172.072 |
| man.off | 17495 | 1.59015 | 187519 | 148.358 |
3.2、十个源点
| Model | Number of Vertices | Average Construction Time (s) | Average Queries Per Second | Peak Memory Usage (MB) |
|---|---|---|---|---|
| ellipsoid.off | 162 | 0.00321017 | 911025 | 0.245674 |
| anchor.off | 519 | 0.03601 | 353062 | 3.19274 |
| rotor.off | 600 | 0.015864 | 805416 | 1.97554 |
| spool.off | 649 | 0.0165743 | 802701 | 2.09675 |
| handle.off | 1165 | 0.0294564 | 646057 | 4.62122 |
| couplingdown.off | 1841 | 0.126045 | 272465 | 7.80517 |
| bones.off | 2154 | 0.055434 | 536646 | 4.0203 |
| mushroom.off | 2337 | 0.139285 | 290425 | 11.462 |
| elephant.off | 2775 | 0.167269 | 285076 | 11.2743 |
| cow.off | 2904 | 0.15432 | 328549 | 13.0676 |
| knot1.off | 3200 | 0.114051 | 454640 | 16.1735 |
| retinal.off | 3643 | 0.233208 | 287869 | 18.6274 |
| femur.off | 3897 | 0.128097 | 457112 | 16.8295 |
| knot2.off | 5760 | 0.413548 | 260195 | 33.484 |
| bull.off | 6200 | 0.371713 | 297560 | 30.522 |
| fandisk.off | 6475 | 0.545929 | 223865 | 39.5607 |
| lion-head.off | 8356 | 0.70097 | 229449 | 59.6597 |
| turbine.off | 9210 | 1.35703 | 157301 | 90.7139 |
| man.off | 17495 | 1.75936 | 185194 | 122.541 |
3.3、多源点的构建和查询时间比较
????????以下数字跟踪了随着源点数量的增加,各种测试模型的建设时间、查询时间和峰值内存使用情况。请注意,随着源点数量的增加,这些值都没有显著增加。事实上,在大多数情况下,运行时间和内存会下降。这是因为源点数量的增加往往会导致序列树更加平坦,从而降低运行时间和内存成本。
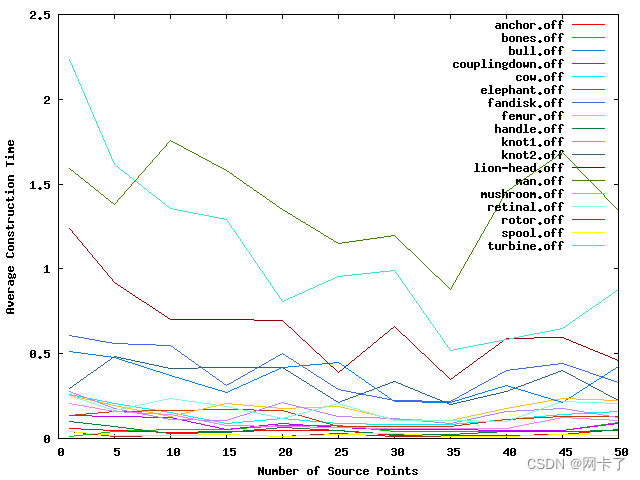
根据不同数量的源点绘制施工时间图。?
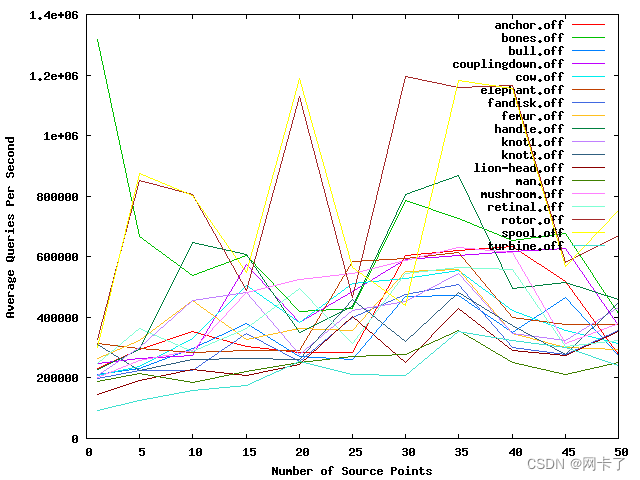
?根据不同数量的源点绘制查询时间。
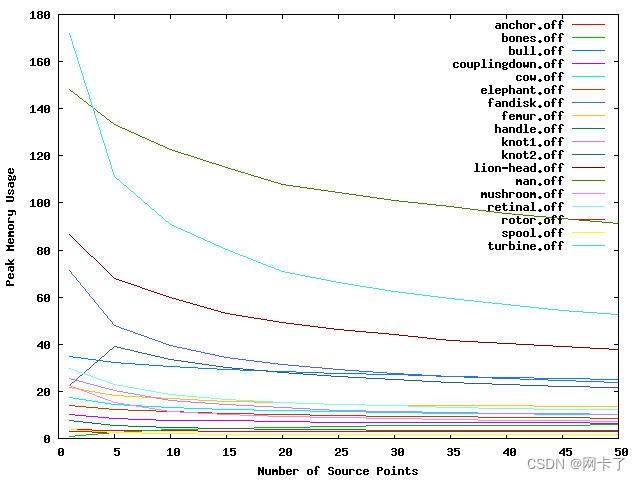
?针对不同数量的源点绘制峰值内存使用情况图。
4、实施细节
4.1、定义
测量路径
????????测地线是某些流形表面上局部最短路径,也就是说,它不能通过一些局部扰动变得更短。在曲面网格上,这转化为一条曲线,当曲线所穿过的面展开到平面时,曲线形成一条直线。另一种描述方法是,在曲线沿线的每个点上,两侧都有π个曲面角(可能除了曲线的端点)。
????????两点之间的测地线不一定是最短路径,但曲面网格上的所有最短路径都是由一个或多个测地线路径的序列组成的,其连接点要么是网格边界上的顶点,要么是鞍点。我们称这种网格曲面上的曲线为其两个端点之间的潜在最短路径。

????????简单曲面网格表面上的测地线。?

同一条测地线,其面展开到平面中。注意,在展开过程中,测地线形成一条直线。?
可视化窗口
????????可见性窗口(或可见性锥)是一对共享一个公共源点并包围曲面网格的局部平坦区域的测地线。局部平坦意味着在窗口内的每对点之间,它们之间恰好有一条测地线路径,该路径也保持在窗口的边界内。因此,在窗口内,可以使用正常的二维欧几里德操作进行距离计算等操作。当可见性窗口遇到顶点(曲面的非平坦部分)时,会出现分支,形成两侧的子窗口。
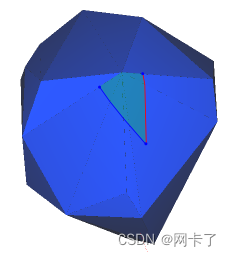
在遇到顶点之前的单个可见性窗口。

遇到凸顶点后,可见性窗口分支到任意一侧(左侧为蓝色,右侧为红色)。请注意,两个新窗口在顶点的另一侧立即重叠,因为周围的表面积小于2π。该重叠区域内的点从原点可能有两条最短的路径。
鞍形顶点
????????曲面网格上的鞍点是一个顶点 v,在该点处,所有面与 v 相交的曲面角度之和大于 2π,或者更简单地说,不能将所有与 v 相交的面无重叠地展平到平面中。识别和处理鞍点在最短路径算法中很重要,因为它们形成了单个测地线曲线无法到达的盲点。
????????为了解决这个问题,我们必须创建一组新的子可见窗口,这些窗口在鞍点周围分支。通过这些子窗口的路径将首先到达鞍点,然后沿着一个新的可见窗口(在曲面上形成一种折线)。请注意,当我们到达非闭合曲面网格的边界顶点时,需要类似的行为。

????????可见性窗口(蓝色阴影)遇到鞍形顶点;顶点后面的红色阴影区域无法通过来自源点的测地线曲线到达(假设测地线必须位于初始窗口内)。?
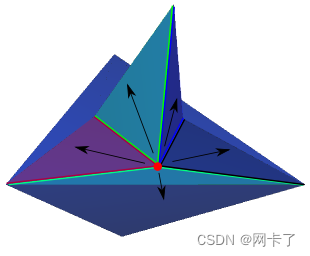
????????为了越过鞍形顶点创建的盲点,我们创建了一个从鞍形顶点发出的可见性窗口的分支集。注意,我们的算法只需要覆盖父可见性窗口盲点的分支。?
序列树
????????为了计算最短路径,我们从每个源点构建一个序列树(或锥树)。序列树通过将所有潜在的最短路径组织成一个可见窗口的层次结构,描述了源自单个源点的所有潜在最短路径的组合结构。
????????每当遇到曲面网格的顶点时,序列树中就会出现一个分支。如果该顶点是一个非鞍点,则只会创建两个子节点,每个子节点对应当前面上与该顶点相交的边。如果该顶点是一个鞍点,除了上述两个子节点外,还会创建一个称为伪源的特殊节点,该节点从该顶点分支出来。
????????一旦构建了序列树,就可以计算从源点到给定可见窗口内每个点的潜在最短路径。沿着树每个分支的面序列被逐个排列到一个公共平面上,这样,使用单个二维欧几里德距离计算就可以得到从曲面上任何点到其最近源点的测地距离。请注意,如果窗口属于伪源,则距离是从目标到伪源测量的,然后测量从伪源到其父级的距离,以此类推,直到原始源。
4.2、整体
????????从任何源点开始的序列树的大小在理论上都是无限的,但我们只关心深度最多为N的树,其中N是表面网格中的面数(因为没有最短路径可以穿过相同的面两次)。即使这样,这个截断的序列树的大小可能是表面网格大小的指数,因此简单的广度优先搜索是不可行的。相反,我们应用技术来消除可以证明不能包含源点最短路径的整个分支。 Xin和Wang [3]的一篇论文中详细介绍了所使用的技术,该论文本身扩展了Chen和Han [1]以及Mitchell、Mount和Papadimitriou [2]的早期工作。
????????处理多个源点很简单,只需要使用类似于多源Dijsktra算法的方法同时构建多个序列树。
4.3、连续Dijkstra
????????连续Dijkstra算法只是将图搜索算法应用于非离散设置。当我们构建搜索树时,新创建的节点被标记为距离度量,并被插入到优先队列中,这样最短距离节点总是排在第一位。
4.4、一个角度,一个拆分
????????Chen和Han的观察表明,在曲面网格的任意给定顶点处出现的所有分支中,只有有限数量的分支具有多个可以定义最短路径的子节点。这是通过为每个顶点维护序列树的所有节点来实现的,这些节点可以在其可见窗口内包含该顶点。
????????对于每个顶点,每个与该顶点相交的面只能出现一个双向分支,具体来说,就是与该顶点相交的最近节点。我们将该最近节点称为该顶点的占据者。
????????如果顶点是鞍点,则该顶点只能建立一个伪源,这次是由距离该顶点最近的绝对节点建立的。
????????仅此方法就可以将序列树构造的构造运行时间减少到多项式时间。
4.5、距离过滤
????????Xin和Wang提出的另一个距离滤波器通过将当前节点的距离与当前面上三个顶点中迄今为止最接近的距离进行比较,有助于进一步修剪搜索树。
4.6、定位最短路径
????????为了定位从目标点到源点的最短路径,我们必须选择正确的可见性窗口。一个简单的方法是跟踪所有与f相交的窗口的每个面f。在实践中,最多有恒定数量的窗口与任何给定的面相交,因此为了简单起见,这是我们使用的方法。另一种选择是在每个面上构造类似Voronoi的结构,其中每个单元表示一个可见性窗口。我们没有尝试这种方法,但它似乎没有计算效益。
5、其他
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 配置多线程,速度一定会更快吗?不!
- 2分钟快速了解Redis核心内容
- 07 整合SSM的快速理解
- 技术经验|Java基础之LocalDate类
- flutter dio使用proxyman抓包进行网络调试
- 进程和线程和协程区别
- 基于gamma矫正的照片亮度调整(python和opencv实现)
- 游戏软文推广:软文推广如何点燃玩家热情
- 【从零开始的新手之旅】:2023西工大计算机系统基础实验之前言
- leetcode:三数之和---双指针