【Leetcode】接雨水（双指针、单调栈）

目录

💡题目描述

💡双指针解法

💡单调栈解法

---

💡题目描述

给定?n?个非负整数表示每个宽度为?1?的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

提示：

• n == height.length
• 1 <= n <= 2 * 104
• 0 <= height[i] <= 105

💡双指针解法

思路：

假设每个宽度为1的柱子那里有一个高度未知的宽度为1的水桶，这个水桶能接的水就是当前柱子所处位置能留下的雨水，而水桶的左边木板的高度取决于当前柱子左边所有的柱子中最高的那个柱子的高度，水桶右边木板的高度取决于当前柱子右边所有的柱子中最高的柱子的高度，而水桶左右木板中较小的那个木板的高度减去当前柱子的高度就是当前水桶能接到的水，也就是当前位置留下的雨水。

class Solution {
public:
    int trap(vector<int>& height) {
        int n=height.size();
        vector<int>pmax(n,0);
        vector<int>smax(n,0);
        pmax[0]=height[0];
        for(int i=1;i<n;i++)
        {
            pmax[i]=max(pmax[i-1],height[i]);//计算前缀最大值
        }
        smax[n-1]=height[n-1];
        for(int i=n-2;i>=0;i--)
        {
            smax[i]=max(height[i],smax[i+1]);//计算后缀最大值
        }
        int ans=0;
        for(int i=0;i<n;i++)
        {
            ans+=(min(pmax[i],smax[i])-height[i]);
        }
        return ans;
    }
};

时间复杂度：O(n)

空间复杂度：O(n)

优化：

上一个解法需要用到两个大小为n的数组分别记录前缀最大值和后缀最大值，而事实上我们可以在左右指针遍历的同时分别记录左边前缀最大值和右边后缀最大值，如果左边前缀最大值小于右边后缀最大值，那么可以计算左边所能接的雨水，计算方法和上面一样，这里就是左边木板高度较小，就可以直接减去柱子高度，否则，计算右边所能接的雨水，左右最大高度相等时随便计算哪一边都是可以的。

class Solution {
public:
    int trap(vector<int>& height) {
        /*假设有一个宽为1的水桶放在每一个柱子那里，高度未知
        每个水桶接的水的多少取决于当前柱子高度和
        它左右区间中分别的最大的柱子高度中较小的那个柱子高度之差，
        例如假设当前柱子高度为1，左边最大的柱子高度为3，右边最大柱子高度为2，
        当前柱子这里的水桶能接的水量为（2-1）=1*/
        int n=height.size();
        int pmax=0;
        int smax=0;
        int l=0;
        int r=n-1;
        int ans=0;
        int i=0;
        while(l<r)
        {
            pmax=max(pmax,height[l]);
            smax=max(smax,height[r]);
            if(pmax<smax)
            {
            ans+=pmax-height[l];
            l++;
            }
            else
            {
                ans+=smax-height[r];
                r--;
            }
        }
        return ans;
    }
};

💡单调栈解法

思路：

这个方法的思路就是求每个凹槽的面积，即横向求解（上一个方法是纵向求解），要得到凹槽的面积，就要求出当前柱子左右两边第一个比它高的柱子，想到这里，就会发现其实很适合用单调栈的方法来求解。

对于这个单调栈，到底是用递增栈还是递减栈呢？

由于我们是要找到当前柱子左右两边第一个比它高的柱子，当我们没有找到比它高的柱子的时候，是会把这个柱子的高度入栈的，一旦发现添加的柱子高度大于栈顶元素了，此时就出现凹槽了，栈顶元素就是凹槽底部的柱子，栈顶第二个元素就是凹槽左边的柱子，而添加的元素就是凹槽右边的柱子。而遇到相同元素时，可以更新栈内元素，也可以选择不处理。

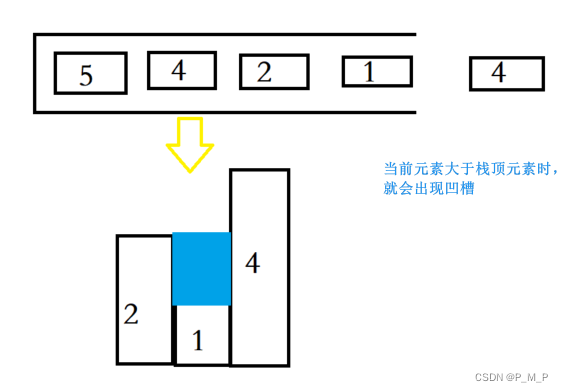
栈内是存储柱子的高度还是下标呢？

这里选择存下标，因为我们要求的是面积，存下标既可以得到凹槽的宽度，也可以得到凹槽的高度，而凹槽的高度是这个柱子左右两边第一个比它高的柱子的高度中较小的那一个减去它的高度，

对于栈顶元素和当前柱子的高度主要有三种情况：

• 情况一：当前遍历的元素（柱子）高度小于栈顶元素的高度 height[i] < height[st.top()]，此时选择入栈。
• 情况二：当前遍历的元素（柱子）高度等于栈顶元素的高度 height[i] == height[st.top()]，此时可以选择更新栈内元素的下标。
• 情况三：当前遍历的元素（柱子）高度大于栈顶元素的高度 height[i] > height[st.top()]，此时就出现凹槽了，计算凹槽面积。

可以发现栈顶和栈顶的下一个元素以及要入栈的元素，这三个元素来接雨水！

具体代码：

class Solution {
public:
    int trap(vector<int>& height) {
        int n=height.size();
        stack<int>st;//单调递增栈
        st.push(0);
        int sum=0;
        for(int i=1;i<n;i++)
        {
            if(height[i]<height[st.top()])
            {
                st.push(i);
            }
            else if(height[i]==height[st.top()])
            {
                st.pop();
                st.push(i);//更新相同高度柱子的下标
            }
            else
            {
                while(!st.empty()&&height[i]>height[st.top()])
                {
                    int mid=st.top();
                    st.pop();
                    if(!st.empty())
                    {
                        int l=min(height[st.top()],height[i])-height[mid];
                        int w=i-st.top()-1;
                        sum+=l*w;
                    }
                }
            }
            st.push(i);
        }
        return sum;
    }
};