day17 平衡二叉树 二叉树的所有路径 左叶子之和

题目1：110 平衡二叉树

题目链接：110 平衡二叉树

题意

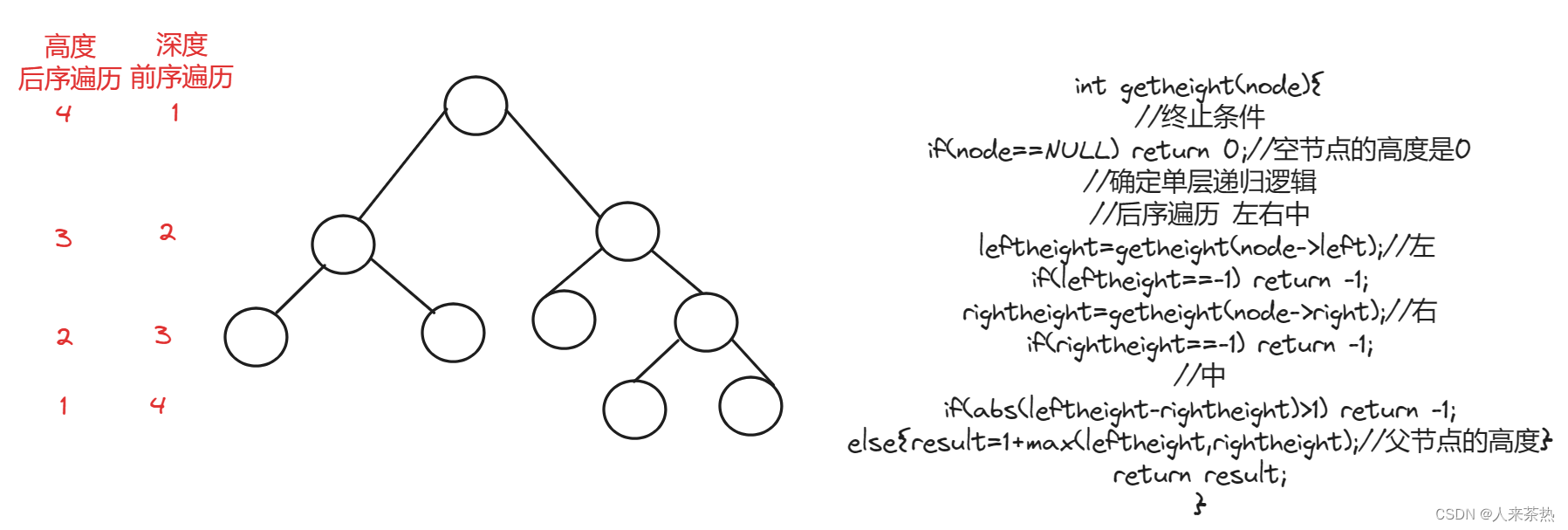
判断二叉树是否为平衡二叉树（每个节点的左右两个子树的高度差绝对值不超过1）

递归遍历

递归三部曲

1）确定递归函数的参数和返回值

2）确定终止条件

3）确定单层递归逻辑

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int getheight(TreeNode* node){
        //终止条件
        if(node==NULL) return 0;
        int result = 0;//result一定要提前定义,是一个全局变量，最终return
        //单层递归逻辑 后序遍历  左右中
        int leftheight = getheight(node->left);//左
        if(leftheight==-1) return -1;
        int rightheight = getheight(node->right);//右
        if(rightheight==-1) return -1;
        //中
        if(abs(rightheight-leftheight)>1) return -1;
        else{
            result = 1 + max(leftheight,rightheight);
        }
        return result;
    }
    bool isBalanced(TreeNode* root) {
        int result = getheight(root);
        if(result==-1) return false;
        else return true;
    }
};

题目2：257 二叉树的所有路径

题目链接：257 二叉树的所有路径

题意

根据二叉树的根节点root，返回所有从根节点到叶子节点的路径（顺序任意）

递归

递归三部曲

1）确定递归函数的参数和返回值

2）确定终止条件

3）确定单层递归逻辑

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void traversal(TreeNode* node,vector<int>& path,vector<string>& result){
        //中 加入后面终止条件的叶子节点
        path.push_back(node->val);//node->val是整型的数字
        //终止条件，遇到叶子节点就终止
        if(node->left==NULL && node->right==NULL){
            //将path放入到result中，注意转换类型，添加->
            string spath;
            for(int i=0;i<path.size()-1;i++){
                spath += to_string(path[i]);
                spath += "->";
            }
            spath += to_string(path[path.size()-1]);//加入最后一个，因为后面没有->，所以单独加入
            result.push_back(spath);
            return;
        }
        //单层递归逻辑  前序遍历   中左右
        if(node->left){
            traversal(node->left,path,result);//左
            path.pop_back();//回溯
        }
        if(node->right){
            traversal(node->right,path,result);//右
            path.pop_back();//回溯
        } 
    }   
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<int> path;
        vector<string> result;
        if(root==NULL) return result;
        traversal(root,path,result);
        return result;
    }
};

隐藏回溯

使用的是?string path，这里并没有加上引用&?，即本层递归中，path + 该节点数值，但该层递归结束，上一层path的数值并不会受到任何影响

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void traversal(TreeNode* node,string path,vector<string>& result){
        //中 加入后面终止条件的叶子节点
        path += to_string(node->val);//node->val是整型的数字
        //终止条件，遇到叶子节点就终止
        if(node->left==NULL && node->right==NULL){
            //将path放入到result中，注意转换类型，添加->
            result.push_back(path);
            return;
        }
        //单层递归逻辑  前序遍历   中左右
        if(node->left){
            traversal(node->left,path+"->",result);//左
            //path.pop_back();//回溯
        }
        if(node->right){
            traversal(node->right,path+"->",result);//右
            //path.pop_back();//回溯
        } 
    }   
    vector<string> binaryTreePaths(TreeNode* root) {
        string path;
        vector<string> result;
        if(root==NULL) return result;
        traversal(root,path,result);
        return result;
    }
};

非隐藏回溯

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void traversal(TreeNode* node,string path,vector<string>& result){
        //中 加入后面终止条件的叶子节点
        path += to_string(node->val);//node->val是整型的数字
        //终止条件，遇到叶子节点就终止
        if(node->left==NULL && node->right==NULL){
            //将path放入到result中，注意转换类型，添加->
            result.push_back(path);
            return;
        }
        //单层递归逻辑  前序遍历   中左右
        if(node->left){
            path = path + "->";
            traversal(node->left,path,result);//左
            path.pop_back();//回溯 >
            path.pop_back();//回溯 -
        }
        if(node->right){
            path = path + "->";
            traversal(node->right,path,result);//右
            path.pop_back();//回溯  >
            path.pop_back();//回溯  -
        } 
    }   
    vector<string> binaryTreePaths(TreeNode* root) {
        string path;
        vector<string> result;
        if(root==NULL) return result;
        traversal(root,path,result);
        return result;
    }
};

题目3：404? 左叶子之和

题目链接：404 左叶子之和

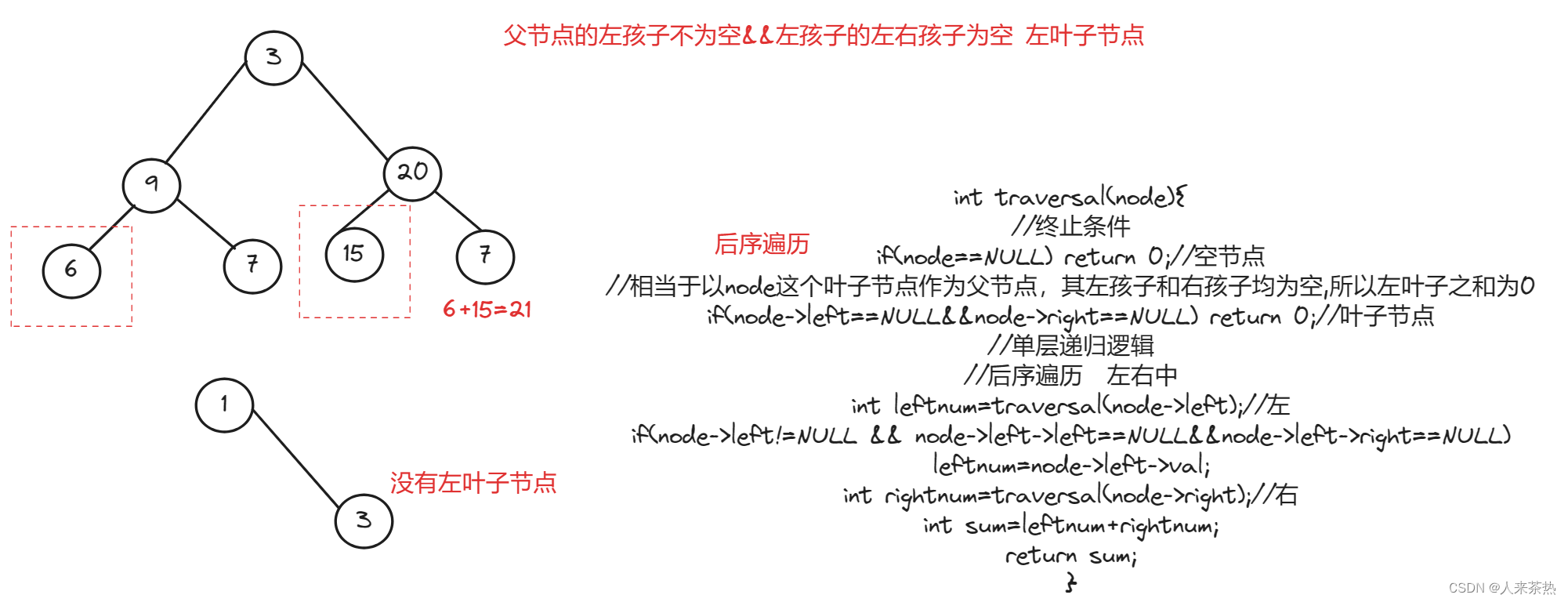
题意

返回所有左叶子之和

一定要是叶子节点? 且是父节点的左孩子，因此必须通过节点的父节点判断当前节点是否为左叶子

递归

递归三部曲

1）确定递归函数的参数和返回值

2）确定终止条件

3）确定单层递归逻辑

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
       //终止条件
       if(root==NULL) return 0;
       if(root->left==NULL && root->right==NULL) return 0;
       //单层递归逻辑  后序遍历  左右中
       //左
       int leftnum = sumOfLeftLeaves(root->left);
       if(root->left!=NULL && root->left->left==NULL && root->left->right==NULL) 
       leftnum = root->left->val;
       //右
       int rightnum = sumOfLeftLeaves(root->right);
       //中
       int sum = leftnum + rightnum;
       return sum;
    }
};

迭代

因为用递归可以做的，栈也可以?

这里栈只是一个容器，换成队列也可?

前序遍历

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
       stack<TreeNode*> st;
       if(root!=NULL) st.push(root);
       int sum = 0;
       while(!st.empty()){
           TreeNode* node = st.top();
           st.pop();
           if(node->left!=NULL && node->left->left==NULL && node->left->right==NULL){
               sum += node->left->val;
           }
           if(node->left) st.push(node->left);
           if(node->right) st.push(node->right);
       }
       return sum;
    }
};

后序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
       stack<TreeNode*> st;
       if(root!=NULL) st.push(root);
       int sum = 0;
       while(!st.empty()){
           TreeNode* node = st.top();
           st.pop();
           if(node->left) st.push(node->left);
           if(node->right) st.push(node->right);
           if(node->left!=NULL && node->left->left==NULL && node->left->right==NULL){
               sum += node->left->val;
           }
       }
       return sum;
    }
};